Giáo Án Dạy Thêm Hè Toán 7 Lên 8
Có thể bạn quan tâm
Giáo Án Dạy Thêm Hè Toán 7 Lên 8 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Giáo án dạy thêm hè toán 7 lên 8 là một chương trình đặc biệt được thiết kế để giúp các bạn học sinh lớp 7 nắm vững kiến thức toán học và chuẩn bị cho khóa học toán lớp 8. Chương trình này tập trung vào việc ôn tập và củng cố những kiến thức cơ bản từ lớp 7 và mở rộng kiến thức mới để chuẩn bị cho những khái niệm phức tạp hơn trong lớp 8.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
ĐỀ CƯƠNG ÔN TẬP TOÁN 7 TRONG HÈ
PHẦN I: ĐẠI SỐ
A. CÁC BÀI TẬP VỀ TÍNH TOÁN
Bài 1: Thực hiện phép tính:
a)
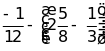 ;
b)
;
b)
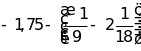 ; c)
; c)
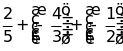 ;
;
d)
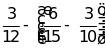 e)
e)
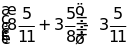 f)
f)
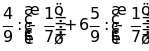
g)
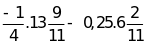 h)
h)
 i)
i)
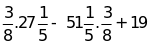
Bài 2: Thực hiện phép tính:
a)
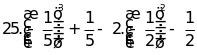 b)
b)

c)
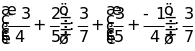 d)
d)
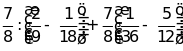
e)
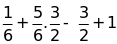 f)
f)

Bài 3: Thực hiện phép tính:
a)
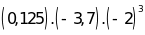 b)
b)
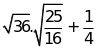
c)
 d)
d)

Bài 4: Thực hiện phép tính:
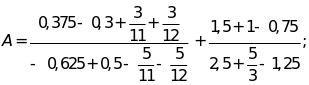
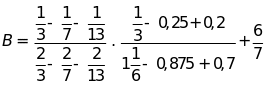
Bài 5: Tìm x biết:
a)
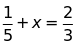 b)
b)
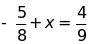 c)
c)

d)
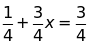 e)
e)
 ` f)
` f)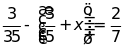
g) h)
h)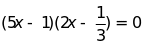
Bài 6: Tìm x biết:
a)
 b)
b)
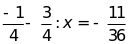
c)
 d)
d)

Bài 7: Tìm x biết:
a)
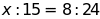 b)
b)
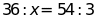 c)
c)

d)
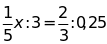 e)
e)
 f)
f)

Bài 8 : Tìm x biết:
a)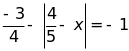 b)
b)
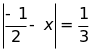 c)
c)
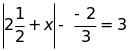
d)
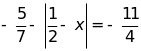 e)
e)
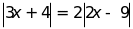 f)
f)

g)
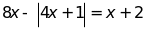 h)
h)
 i)
i)

Bài 9 : Tìm x biết
a)
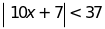 b)
b)
 c)
c)
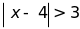
Bài 10 : Tìm x biết
a)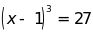 ; b)
; b)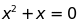 ; c)
; c)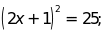
d)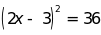 ; e)
; e)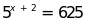 ; f)
; f)

g) ; h)
; h)
 ;
;
Bài 10: Tìm số nguyên dương n biết
a)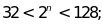 b)
b)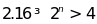 ; c)
; c)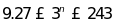 .
.
Bài
11:
Cho
P =
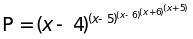 Tính P khi
Tính P khi

Bài
12:
So
sánh a)
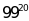 và
và
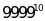 ; b)
; b)
 và
và
 ; c)
; c)
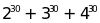 và
và
 .
.
B. CÁC BÀI TẬP VỀ ĐẠI LƯỢNG TỶ LỆ
Bài 1: Tìm x , y, biết
a)
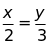 và
và
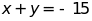 b)
b)
 và
và
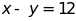
c)
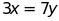 và
và
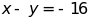 d)
d)
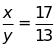 và
và

e)
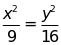 và
và
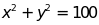
Bài 2: Tìm x , y, z biết
a)
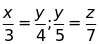 và
và
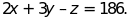
b)
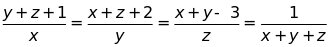
c)
 và
và

d)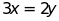 ;
;
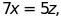
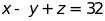
e)
 và
và
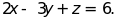
g)
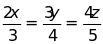 và
và
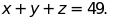
h)
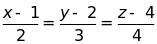 và
và
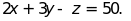
i)
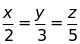 và
và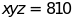 .
.
Bài
3:
Cho
x và y là hai đại lượng tỉ lệ thuận:
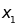 và
và
 là hai giá trị khác nhau của x;
là hai giá trị khác nhau của x;
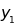 và
và
 là hai giá trị tương ứng của y.
là hai giá trị tương ứng của y.
a.Tính
 biết
biết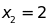 ;
;
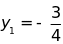 và
và

b.
Tính
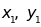 biết rằng:
biết rằng: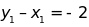 ;
;
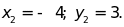
Bài 4: Cho x và y là hai đại lượng tỉ lệ thuận.
a)
Viết công thức liên hệ giữa y và x biết rằng tổng
hai giá trị tương ứng của x bằng 4k thì tổng hai giá
trị tương ứng của y bằng
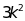 ( k ≠
0).
( k ≠
0).
b)
Với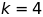 ;
;
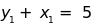 , hãy tìm
, hãy tìm
 và
và .
.
Bài 5: Chu vi một tam giác là 60cm. Các đường cao có độ dài là 12cm; 15cm; 20cm. Tính độ dài mỗi cạnh của tam giác đó.
Bài 6: Một xe ôtô khởi hành từ A, dự định chạy với vận tốc 60km/h thì sẽ tới B lúc 11giờ. Sau khi chạy được nửa đường thì vì đường hẹp và xấu nên vận tốc ôtô giảm xuống còn 40km/h do đó đến 11 giờ xe vẫn còn cách B là 40km.
a/ Tính khoảng cách AB b/ Xe khởi hành lúc mấy giờ?
Bài 7: Một đơn vị làm đường, lúc đầu đặt kế hoạch giao cho ba đội I, II, III , mỗi đội làm một đoạn đường có chiều dài tỉ lệ (thuận) với 7, 8, 9. Nhưng về sau do thiết bị máy móc và nhân lực của các đội thay đổi nên kế hoạch đã được điều chỉnh, mỗi đội làm một đoạn đường có chiều dài tỉ lệ (thuận) với 6, 7, 8. Như vậy đội III phải làm hơn so với kế hoạch ban đầu là 0,5km đường. Tính chiều dài đoạn đường mà mỗi đội phải làm theo kế hoạch mới.
C. CÁC BÀI TOÁN LIÊN QUAN ĐẾN HÀM SỐ :
Bài
1:
Cho hàm số
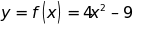
a.
Tính

 b. Tìm x để
b. Tìm x để
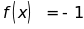
c.
Chứng tỏ rằng với
 thì
thì

Bài
2:
Viết công thức của hàm số
 biết rằng y tỷ lệ thuận với x theo hệ số tỷ lệ
biết rằng y tỷ lệ thuận với x theo hệ số tỷ lệ
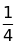
a.
Tìm x để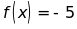 b. Chứng tỏ rằng nếu
b. Chứng tỏ rằng nếu
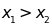 thì
thì
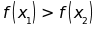
Bài
3:
Viết công thức của hàm số
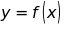 biết
rằng y tỉ lệ nghịch với x theo hệ số
biết
rằng y tỉ lệ nghịch với x theo hệ số
 .
.
a.Tìm
x để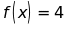 ;
;
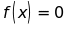 b. Chứng tỏ rằng
b. Chứng tỏ rằng
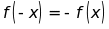
Bài
4:
Cho hàm số
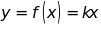 (k là hằng số,
(k là hằng số,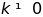 ).
Chứng minh rằng:
).
Chứng minh rằng:
a)
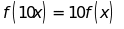 b)
b)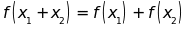 c)
c)

D. MẶT PHẲNG TỌA ĐỘ
Bài
1:
Đồ thị hàm số
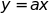 đi qua điểm
đi qua điểm
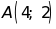
a) Xác định hệ số a và vẽ đồ thị của hàm số đó.
b)
Cho
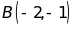 ;
;
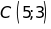 Không cần biểu diễn B và C trên mặt phẳng tọa độ,
hãy cho biết ba điểm A, B, C có thẳng hàng không?
Không cần biểu diễn B và C trên mặt phẳng tọa độ,
hãy cho biết ba điểm A, B, C có thẳng hàng không?
Bài
2:
Cho các hàm số
 và
và
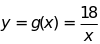 .
Không vẽ đồ thị của chúng em hãy tính tọa độ giao
điểm của hai đồ thị.
.
Không vẽ đồ thị của chúng em hãy tính tọa độ giao
điểm của hai đồ thị.
Bài
3:
Cho hàm số:
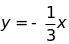 a.
Vẽ đồ thị của hàm số.
a.
Vẽ đồ thị của hàm số.
b.
Trong các điểm

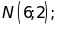
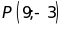 điểm
nào thuộc đồ thị (không
vẽ các điểm đó)
điểm
nào thuộc đồ thị (không
vẽ các điểm đó)
Bài
4:
Vẽ đồ thị của hàm số
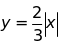
E. BIỂU THỨC ĐẠI SỐ - ĐƠN THỨC – ĐA THỨC
Đa thỨc mỘt biẾn. CỘng vÀ trỪ Đa thỨc mỘt biẾn
1. bIỂU THỨC ĐẠI SỐ
Bài
1:
Tính giá trị của biểu thức:
 với
với
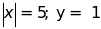
Bài
2:
Cho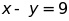 , tính giá trị của biểu thức :
, tính giá trị của biểu thức :
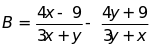

Bài 3: Xác định giá trị của biểu thức để các biểu thức sau có nghĩa:
a)
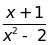 ; b)
; b)
 ; c)
; c)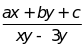 d)
d)
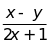
Bài
4:
Tính giá trị của biểu thức
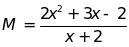 tại: a)
tại: a)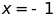 ; b)
; b)

Bài
5:
Cho đa thức

a.
Tính giá trị của P với
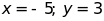
b. Chứng minh rằng P luôn luôn nhận giá trị không âm với mọi x, y
Bài
6:
a. Tìm GTNN của biểu thức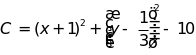
b.Tìm
GTLN của biểu thức
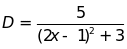
Bài
7:
Cho biểu thức
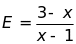 .
Tìm các giá trị nguyên của x để:
.
Tìm các giá trị nguyên của x để:
a. E có giá trị nguyên b. E có giá trị nhỏ nhất
2. ĐƠN THỨC - TÍCH CÁC ĐƠN THỨC
Bài
1:
Cho các đơn thức
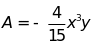 ;
;
 .
.
Có các cặp giá trị nào của x và y làm cho A và B cùng có giá trị âm không?
Bài 2: Thu gọn các đơn thức trong biểu thức đại số.
a)

b)
 (với
(với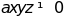 )
)
Bài 3: Tính tích các đơn thức rồi cho biết hệ số và bậc của đơn thức đối với tập hợp các biến số (a, b, c là hằng)
a)
 ;
b)
;
b)

c)
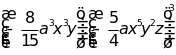
Bài
3:
Cho ba đơn thức:

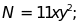
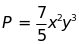 .
Chứng minh rằng ba đơn thức này không thể cùng có giá
trị dương.
.
Chứng minh rằng ba đơn thức này không thể cùng có giá
trị dương.
3. Đơn thỨc đỒng dẠng. TỔng và hiỆu các đơn thỨc đỒng dẠng
Bài
1:
Cho đơn thức

 trong đó m
là hằng số dương.
trong đó m
là hằng số dương.
a. Hai đơn thức A và B có đồng dạng không ?
b.
Tính hiệu

c.
Tính GTNN của hiệu

Bài
2:
Cho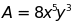 ;
; ;
;
 Chứng minh rằng
Chứng minh rằng
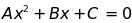
Bài
3:
Chứng minh rằng với
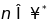
a/
 có tận cùng bằng chữ số 0
có tận cùng bằng chữ số 0
b/
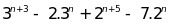 chia hết cho 25
chia hết cho 25
c/
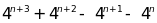 chia hết cho 300
chia hết cho 300
Bài
4:
Viết tích
 thành tổng của ba lũy thừa cơ số 5 với số mũ là ba
số tự nhiên liên tiếp.
thành tổng của ba lũy thừa cơ số 5 với số mũ là ba
số tự nhiên liên tiếp.
Bài
5:
Cho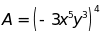 ;
;
 Tìm x, y, z biết
Tìm x, y, z biết

Đa thức một biến
Bài
1:
Cho ;
;
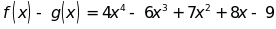
Hãy tìm các đa thức f(x) ; g(x)
Bài
2:
Cho 
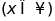
 (
( .
.
Tính
giá trị của hiệu
 tại
tại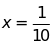
Bài
3:
Cho . Tính
. Tính
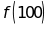
Bài
4:
Cho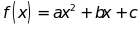 . Biết
. Biết
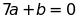 , hỏi
, hỏi
 có thể là số âm không?
có thể là số âm không?
Bài 5: Tam thức bậc hai là đa thức có dạng f(x) = ax + b với a, b, c là hằng, a 0. Hãy xác định các hệ số a, b biết f(1) = 2; f(3) = 8
Bài
6:
Cho 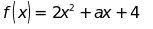 (a là hằng)
(a là hằng)
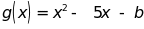 ( b là hằng)
( b là hằng)
Tìm
các hệ số a, b sao cho
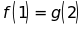 và
và

4. NghiỆm cỦa đa thỨc mỘt biẾn
Bài
1:
Cho hai đa thức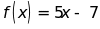 ;
;
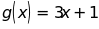
a) Tìm nghiệm của f(x); g(x)
b)
Tìm nghiệm của đa thức

c/
Từ kết quả câu b suy ra với giá trị nào của x thì ?
?
Bài
2:
Cho đa thức

a)
Số
 có phải là nghiệm của f(x) không?
có phải là nghiệm của f(x) không?
b/ Viết tập hợp S tất cả các nghiệm của f(x)
Bài 3: Thu gọn rồi tìm nghiệm của các đa thức sau:
a)
 b)
b)
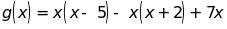
c)

Bài 4: Tìm đa thức f(x) rồi tìm nghiệm của f(x) biết rằng:
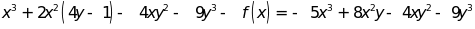
Bài
5:
Cho
2 đa thức:
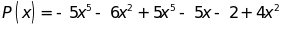
và
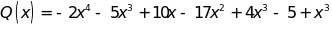
a) Thu gọn mỗi đa thức trên rồi sắp xếp theo lũy thừa giảm dần của biến.
b)
Tính
 .
.
c)
Chứng tỏ
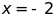 là nghiệm của
là nghiệm của
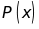 nhưng
không phải là nghiệm của
nhưng
không phải là nghiệm của
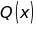 .
.
Bài
6:
Cho
2 đa thức:
và
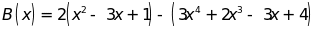
a) Thu gọn rồi sắp xếp theo lũy thừa tăng dần của biến.
b)
Tính
 ;
;
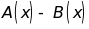 . c)
Tìm nghiệm của
. c)
Tìm nghiệm của
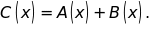
d)
Chứng tỏ đa thức
 vô nghiệm.
vô nghiệm.
Bài
7:
Cho
hai đa thức:
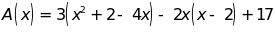
và

a)
Thu gọn
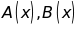 .
Sắp xếp các đa thức theo lũy thừa giảm của biến. Tìm
hệ số cao nhất, hệ số tự do của 2 đa thức đó.
.
Sắp xếp các đa thức theo lũy thừa giảm của biến. Tìm
hệ số cao nhất, hệ số tự do của 2 đa thức đó.
b)
Tìm
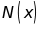 sao cho
sao cho
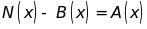 và
và
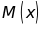 sao cho
sao cho
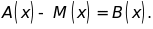
c)
Chứng minh:
 là một nghiệm của
là một nghiệm của
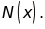 Tìm
một nghiệm nữa của
Tìm
một nghiệm nữa của

d)
Tính nghiệm của
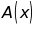 tại
tại
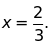
HÌNH HỌC – BÀI TẬP TỔNG HỢP
Bài
1: Trên
cạnh Ox và Oy của góc xOy lấy hai điểm A và B sao cho
 tia phân giác góc Oz của góc
tia phân giác góc Oz của góc
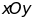 cắt AB tại C.
cắt AB tại C.
a) Chứng minh C là trung điểm của AB và AB vuông góc với OC.
b)
Trên tia Cz lấy điểm M sao cho
 . Chứng minh:
. Chứng minh:

c) Kẻ MI vuông góc với Oy, MK vuông góc với Ox. So sánh BI và AK.
d) Gọi N là giao điểm của AI và BK. Chứng minh O, N, M thẳng hàng.
Bài 2: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC). Gọi N là trung điểm của AC.
a)
Chứng minh

b)
Hai đoạn thẳng BN và AH cắt nhau tại G, trên tia đối
của tia NB lấy K sao cho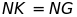 . Chứng minh
. Chứng minh

b) Chứng minh G là trung điểm của BK.
c)
Gọi M là trung điểm AB. Chứng minh

Bài
3: Cho
tam giác ABC có 3 góc nhọn và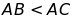 . Tia phân giác của góc A cắt đường trung trực của
đoạn BC tại I. Từ I vẽ IM vuông góc với AB và IN vuông
góc với AC. Trên tia đối của tia CA lấy điểm E sao cho
. Tia phân giác của góc A cắt đường trung trực của
đoạn BC tại I. Từ I vẽ IM vuông góc với AB và IN vuông
góc với AC. Trên tia đối của tia CA lấy điểm E sao cho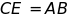 .
.
Chứng minh
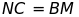
Chứng minh IN là đường trung trực của AE.
Gọi F là giao điểm của BC và AI. Chứng minh
 .
.
Bài
4: Cho
tam giác ABC cân tại A, đường cao BH. Trên đáy BC lấy M,
vẽ
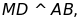
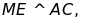

Chứng minh


Khi M chạy trên đáy BC thì tổng
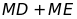 có giá trị không đổi.
có giá trị không đổi.Trên tia đối của tia CA lấy điểm K sao cho
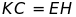 . Chứng minh trung điểm của KD nằm trên cạnh BC.
. Chứng minh trung điểm của KD nằm trên cạnh BC.
Bài
5: Cho
tam giác ABC cân tại A có góc A bằng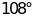 .
.
Tính số đo các góc B và góc C?
Gọi O là giao điểm của hai đường trung trực cạnh AB và AC. I là giao điểm của các đường phân giác trong tam giác. Chứng minh A, O, I thẳng hàng.
Chứng minh BC là đường trung trực của đoạn thẳng OI.
Bài
6: Cho
tam giác ABC vuông tại A có
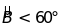 Kẻ đường cao AH của tam giác ABC, kẻ đường phân giác
AK của tam giác AHC. Kẻ
Kẻ đường cao AH của tam giác ABC, kẻ đường phân giác
AK của tam giác AHC. Kẻ
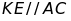 (E thuộc AB), KE cắt AH tại I. Kẻ đường thẳng vuông
góc với AK tại K cắt AC tại D. Chứng minh rằng:
(E thuộc AB), KE cắt AH tại I. Kẻ đường thẳng vuông
góc với AK tại K cắt AC tại D. Chứng minh rằng:

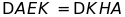
BI là tia phân giác của
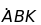
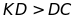
Bài 7: Cho tam giác DEF cân tại D, đường phân giác DI.Gọi N là trung điểm của IF. Vẽ điểm M sao cho N là trung điểm của DM. Chứng minh rằng:
a)
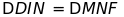 ;
;

b)
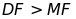
c)
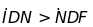
d) D, I, K thẳng hàng ( K là trung điểm của ME).
Bài 8: Cho tam giác ABC vuông tại A. Vẽ ra phía ngoài tam giác ABC các tam giác ABD và ACE lần lượt vuông cân tại D và E. Gọi M là trung điểm BC, F là giao điểm của MD và AB, K là giao điểm của ME và AC.
Chứng minh ba điểm D, A, E thẳng hàng.
Chứng minh
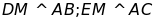
Tam giác DME là tam giác gì?
Tam giác vuông ABC cần thỏa mãn điều kiện gì để A là trung điểm của ED?
Bài
9: Cho
tam giác ABC nhọn . Kẻ
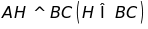 .
Vẽ điểm D sao cho AB là đường trung trực của DH. Vẽ
điểm E sao cho AC là đường trung trực của EH. Nối DE
cắt AB, AC theo thứ tự tại I và K, DH cắt AB tại M.
Chứng minh rằng:
.
Vẽ điểm D sao cho AB là đường trung trực của DH. Vẽ
điểm E sao cho AC là đường trung trực của EH. Nối DE
cắt AB, AC theo thứ tự tại I và K, DH cắt AB tại M.
Chứng minh rằng:

IA và KA là các tia phân giác góc ngoài tại đỉnh I và K của tam giác IHK
HA là tia phân giác của góc IHK.
HA; IC; KB đồng quy.
Bài
10: Cho
tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy
điểm D sao cho . Đường vuông góc với BC tại D cắt AC tại E. Chứng
minh rằng:
. Đường vuông góc với BC tại D cắt AC tại E. Chứng
minh rằng:
Điểm H nằm giữa B; D.
BE là đường trung trực của đoạn AD.
Tia AD là tia phân giác của góc HAC.
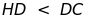
Bài
11: Cho
tam giác ABC vuông tại A,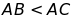 . Lấy điểm D sao cho A là trung điểm của BD.
. Lấy điểm D sao cho A là trung điểm của BD.
Chứng minh CA là tia phân giác của góc BCD
Vẽ BE vuông góc với CD tại E, BE cắt CA tại I. Vẽ IF vuông góc với CB tại F. Chứng minh
 cân và EF song song với DB
cân và EF song song với DBSo sánh IE và IB
Tìm điều kiện của tam giác ABC để tam giác BEF cân tại F.
Bài
12: Cho
 ,
phân giác Ot. Từ điểm A trên tia Ot kẻ
,
phân giác Ot. Từ điểm A trên tia Ot kẻ
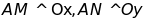 .
Đường thẳng AM cắt tia đối của tia Oy tại B, đường
thẳng AN cắt tia đối của tia Ox tại C.
.
Đường thẳng AM cắt tia đối của tia Oy tại B, đường
thẳng AN cắt tia đối của tia Ox tại C.
Chứng minh OA=OB=OC
Tam giác ABC là tam giác gì?
Chứng minh MN//BC
Bài 13: Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm.
a) Tam giác ABC là tam giác gì? Vì sao?
b)
Kẻ AH
vuông góc với BC
(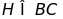 ).
Gọi AD
là phân giác
).
Gọi AD
là phân giác
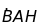 (
(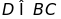 ).
Qua A
vẽ đường thẳng song song với BC,
trên đó lấy E
sao cho AE
= BD (E
và C
cùng phía đối với AB).
CMR: AB
= DE.
).
Qua A
vẽ đường thẳng song song với BC,
trên đó lấy E
sao cho AE
= BD (E
và C
cùng phía đối với AB).
CMR: AB
= DE.
c)
CMR:
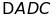 cân.
cân.
d) Gọi M là trung điểm AD, I là giao điểm của AH và DE. CMR: C, I, M thẳng hàng.
Bài 14. Cho tam giác ABC vuông tại A, phân giác BD, kẻ DE vuông góc với BC tại E. Trên tia đối của tia AB lấy F sao cho AF = CE. CMR:
a)
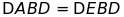
b) BD là đường trung trực của AE.
c) .
.
d)
E, D, F thẳng hàng và
 .
.
e) 2(AD + AF) > CF.
Bài
15. Cho
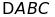 có
có
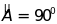 và
và
 .
Kẻ
.
Kẻ
 .
Trên tia
.
Trên tia
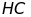 lấy
điểm
lấy
điểm
 sao cho
sao cho
 .
Kẻ
.
Kẻ
 kéo dài (
kéo dài (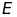 thuộc tia
thuộc tia
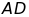 ).
Chứng minh:
).
Chứng minh:
a)
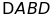 cân.
cân.
b)
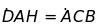
c)
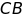 là tia phân giác của
là tia phân giác của
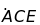
d)
Kẻ
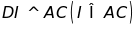 ,
chứng minh 3 đường thẳng
,
chứng minh 3 đường thẳng
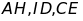 đồng quy.
đồng quy.
e)
So sánh
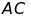 và
và
 .
.
f)
Tìm điều kiện của
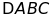 để
để
 là trung điểm
là trung điểm
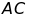 .
.
Bài
16. Cho
 cân tại
cân tại (
(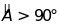 ).
Trên cạnh
).
Trên cạnh
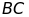 lấy 2 điểm
lấy 2 điểm
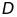 ,
,
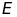 sao cho
sao cho
 .
Kẻ
.
Kẻ
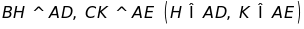 ,
,
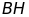 cắt
cắt
 tại
tại
 .
.
Chứng minh rằng:
a)
 cân.
cân.
b)
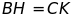 .
.
c)
Gọi
 là trung điểm của
là trung điểm của
 .
Chứng minh
.
Chứng minh
 thẳng hàng.
thẳng hàng.
d)
 .
.
e)
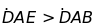 .
.
Bài
17. Cho
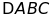 đều. Tia phân giác góc
đều. Tia phân giác góc
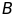 cắt
cắt
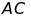 tại
tại
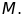 Từ
Từ
 kẻ đường thẳng vuông góc với
kẻ đường thẳng vuông góc với
 cắt
cắt
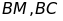 tại
tại
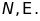 Chứng
minh:
Chứng
minh:
a)
 cân.
cân.
b)

c)
Xác định dạng của tam giác
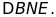
d)
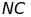 là trung trực của
là trung trực của

e)
Cho
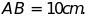 Tính
diện tích
Tính
diện tích
 và chu vi
và chu vi

Bài
18. Cho
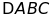 có
có
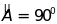 (
( ),
đường cao
),
đường cao
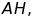
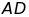 là phân giác của
là phân giác của
 .
Kẻ
.
Kẻ
 .
.
a)
Chứng minh:
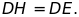
b)
Gọi
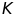 là giao điểm của
là giao điểm của
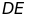 và
và
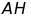 .
Chứng minh
.
Chứng minh
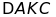 cân.
cân.
c)
Chứng minh
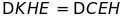 .
.
d)
Cho
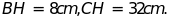 Tính
Tính

e)
Giả sử
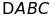 có
có
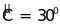 ,
,
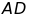 cắt
cắt
 tại
tại
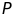 .
Chứng minh
.
Chứng minh
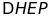 đều.
đều.
Bài
19. Cho
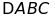 có
có
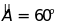 .
Các tia phân giác của góc
.
Các tia phân giác của góc
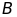 và
và
 cắt nhau ở
cắt nhau ở
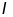 ,
cắt cạnh
,
cắt cạnh
 ở
ở
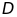 và
và
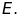 Tia phân giác góc
Tia phân giác góc
 cắt
cắt
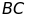 ở
ở
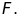
a)
Tính góc
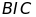
b)
Chứng minh:
 .
.
c)
Chứng minh:
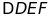 đều.
đều.
d)
Chứng minh:
 là giao điểm các đường phân giác của hai tam giác
là giao điểm các đường phân giác của hai tam giác
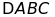 và
và
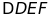
HẾT
Ngoài Giáo Án Dạy Thêm Hè Toán 7 Lên 8 thì các tài liệu học tập trong chương trình 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm






