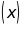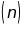Bài Tập Toán Tính Số Trung Bình Cộng Lớp 7 Có Lời Giải
Có thể bạn quan tâm
Bài Tập Toán Tính Số Trung Bình Cộng Lớp 7 Có Lời Giải là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Số trung bình cộng là một khái niệm quan trọng trong toán học. Nó cho chúng ta biết giá trị trung bình của một tập hợp các số. Để tính số trung bình cộng, chúng ta cộng tất cả các số lại và chia tổng đó cho số lượng các số. Kết quả thu được chính là số trung bình cộng của tập hợp đó.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
BẢNG “TẦN SỐ” CÁC GIÁ TRỊ CỦA DẤU HIỆU
I. TÓM TẮT LÝ THUYẾT
Số trung bình cộng của dấu hiệu
Dựa vào bảng “tần số”,
ta có thể tính số trung bình cộng của một dấu hiệu
(kí hiệu là
 )
như sau:
)
như sau:
Nhân từng giá trị với tần số tương ứng;
Cộng tất cả các tích vừa tìm được;
Chia tổng đó cho số các giá trị (tức là tổng các tần số) .
Công thức tính:
 trong đó:
trong đó:
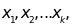 là k giá trị khác nhau của
dấu hiệu X.
là k giá trị khác nhau của
dấu hiệu X.
 là k tần số tương ứng.
N
là số các giá trị.
là k tần số tương ứng.
N
là số các giá trị.
Ý nghĩa của số trung bình cộng.
Số trung bình cộng thường được dung làm “đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
Khi các giá trị của dấu hiệu có khoảng chênh lệch rất lớn đối với nhau thì không nên lấy số trung bình cộng làm “đại diện” cho dấu hiệu đó.
Số trung bình cộng có thể không thuộc dãy giá trị của dấu hiệu.
Mốt của dấu hiệu
Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng “tần số”, kí hiệu là MO.
Có những dấu hiệu có hai mốt hoặc nhiều hơn.
II. BÀI TẬP
Bài 1: Thời gian giải một bài toán của 50 em học sinh được ghi lại trong bảng sau (tính theo phút) :
3 |
10 |
7 |
8 |
12 |
9 |
6 |
8 |
9 |
6 |
4 |
11 |
7 |
8 |
10 |
9 |
5 |
7 |
9 |
6 |
8 |
8 |
6 |
6 |
8 |
8 |
11 |
9 |
10 |
10 |
5 |
6 |
10 |
5 |
8 |
7 |
8 |
9 |
7 |
9 |
7 |
4 |
12 |
5 |
4 |
7 |
9 |
6 |
7 |
6 |
a) Lập bảng “tần số” nêu rõ dấu hiệu và số giá trị của dấu hiệu.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) Tính số trung bình cộng của dấu hiệu.
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 2: Một thầy giáo theo dõi thời gian làm bài tập (tính theo phút) của 30 học sinh và ghi lại như sau:
5 |
9 |
7 |
10 |
10 |
9 |
10 |
9 |
12 |
7 |
10 |
12 |
15 |
5 |
12 |
10 |
7 |
15 |
9 |
10 |
9 |
9 |
10 |
9 |
7 |
12 |
9 |
10 |
12 |
5 |
a) Dấu hiệu ở đây là …………………………………………………………………………
b) Lập bảng “tần số” và nêu nhận xét.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c) Tính số trung bình cộng và tìm mốt của dấu hiệu.
… ………………………………………
………………………………………
…………………………………………
…………………………………………
…………………………………………
…………………………………………
…………………………………………
d) Vẽ biểu đồ đoạn thẳng.
Bài 3: Đo chiều cao của 30 học sinh lớp 7 được kết quả theo bảng
dưới
đây (đơn vị
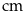 )
:
)
:
Chiều cao (sắp xếp theo khoảng) |
Tần số
|
a) Bảng này có gì khác so với những bảng tần số đã biết ? ……………………………… ……………………………… ……………………………… ……………………………… |
105 |
3 |
|
110-120 |
7 |
|
121-131 |
5 |
|
132-142 |
6 |
|
143-153 |
7 |
|
155 |
2 |
|
|
|
b) Tính số trung bình cộng trong những trường hợp này ?
Trước hết ta tính số trung bình cộng của từng khoảng.
Số đó
chính là trung bình cộng của các giá trị lớn nhất và
nhỏ nhất của khoảng. Ví dụ : trung bình cộng của
khoảng 110-120 là
 …………
…………
- Nhân các số trung bình vừa tìm được với các tần số tương ứng.
- Thực hiện tiếp các bước theo quy tắc đã học.
Để tiện việc tính toán ta kể thêm vào cột chiều cao là cột số trung bình cộng của từng lớp ; sau cột tần số là cột tích giữa trung bình cộng.
Chiều cao |
Trung bình cộng của mỗi lớp |
Tần số |
Tích của trung bình cộng mỗi lớp với tần số |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Số trung
bình cộng là :
 ……………………………………….
……………………………………….
Bài 4: Số cân nặng (tính tròn đến kilogam) của 20 học sinh được ghi lại như sau:
28 |
35 |
29 |
37 |
30 |
35 |
37 |
30 |
35 |
29 |
30 |
37 |
35 |
35 |
42 |
28 |
35 |
29 |
37 |
30 |
a) Dấu hiệu ở đây là gì?
b) Lập bảng “tần số” và nêu nhận xét.
c) Tính số trung bình cộng và tìm mốt của dấu hiệu.
d) Vẽ biểu đồ đoạn thẳng.
Bài 5: Hai xạ thủ A và B mỗi người bắn 15 phát đạn, kết quả (điểm mỗi lần bắn) được ghi lại trong bảng sau:
A |
10 |
8 |
9 |
10 |
10 |
9 |
10 |
8 |
8 |
10 |
10 |
9 |
8 |
10 |
9 |
B |
10 |
9 |
10 |
10 |
10 |
6 |
10 |
10 |
10 |
10 |
7 |
10 |
10 |
10 |
6 |
a) Tính điểm trung bình của từng xạ thủ?
b) Tìm mốt?
c) Có nhận xét gì về kết quả và khả năng của từng người?

HDG:
Bài 1: a) Bảng tần số:
Thời gian
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Tần số
|
1 |
3 |
4 |
8 |
8 |
9 |
8 |
5 |
2 |
2 |
|
Dấu hiệu: Thời gian giải một bài toán của mỗi học sinh (tính theo phút). Số giá trị của dấu hiệu: 50.
b)
 (phút).
(phút).
Bài 2: a) Dấu hiệu: Thời gian làm bài tập của mỗi học sinh.
b) Bảng “tần số”:
-
Thời gian (x)
5
7
9
10
12
15
Tần số (n)
3
4
8
8
5
2
N = 30
Nhận xét:
- Cả 30 học sinh đều làm được bài tập.
- Thời gian làm bài ít nhất: 5 phút.
- Thời gian làm bài nhiều nhất: 15 phút.
- Số đông học sinh làm
xong bài tập trong khoảng từ 9 đến 12 phút
 .
.
c)
Số trung bình cộng
 (phút).
(phút).
Mốt
của dấu hiệu:
 (có hai mốt).
(có hai mốt).
d) Học sinh tự vẽ biểu đồ đoạn thẳng.
Bài 3:
a) Bảng cho giá trị của dấu hiệu dưới dạng khoảng.
b) Trước hết ta tính số trung bình cộng của từng khoảng.
Số đó chính là trung bình cộng của các giá trị lớn nhất và nhỏ nhất của khoảng. Ví dụ : trung bình cộng của khoảng 110-120 là 115
- Nhân các số trung bình vừa tìm được với các tần số tương ứng.
- Thực hiện tiếp các bước theo quy tắc đã học.
Để tiện việc tính toán ta kể thêm vào cột chiều cao là cột số trung bình cộng của từng lớp ; sau cột tần số là cột tích giữa trung bình cộng.
-
Chiều cao
Trung bình cộng của mỗi lớp
Tần số
Tích của trung bình cộng mỗi lớp với tần số

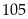

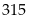
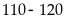
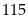



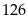

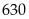






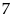
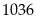


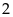
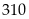
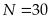
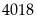
Số trung
bình cộng là :
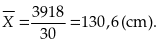
Bài 4:
a) Dấu hiệu: Số cân nặng của mỗi học sinh.
b) Bảng “tần số”:
-
Số cân (x)
28
29
30
35
37
42
Tần số (n)
2
3
4
6
4
1
N = 20
Nhận xét:
- Người nhẹ nhất: 28 kg.
- Người nặng nhất: 42 kg.
-
Số cân nặng của nhiều bạn trong khoảng 30 đến 37 kg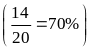 .
.
c)
 (kg);
(kg);
 . d)
Học sinh tự vẽ.
. d)
Học sinh tự vẽ.
Bài 5:
a) Điểm trung bình của xạ thủ A là:
-
Giá trị

Tần số
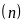
Các tích
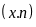
8
4
32
9
4
36
10
7
70
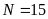
Tổng: 138

Điểm trung bình của xạ thủ B là:
-
Giá trị
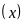
Tần số
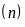
Các tích
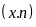
6
2
12
7
1
7
9
1
9
10
11
110
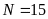
Tổng: 138

b)
Mốt của dấu hiệu
là

c) Nhận xét: hai xạ thủ đều có số điểm trung bình như nhau nhưng xạ thủ A bắn đều hơn (số điểm các lần bắn đều nhau), còn xạ thủ B bắn phân tán hơn (số điểm các lần bắn đôi lúc có sự chênh lệch nhau).
Ngoài Bài Tập Toán Tính Số Trung Bình Cộng Lớp 7 Có Lời Giải thì các tài liệu học tập trong chương trình 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm
| Bài Tập Toán 7 Đơn Thức Có Lời Giải |