Đề Thi Đánh Giá Năng Lực 2023 Đại Học Quốc Gia TP.HCM Môn Toán
Đề Thi Đánh Giá Năng Lực 2023 Đại Học Quốc Gia TP.HCM Môn Toán được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
Kỳ thi Đánh Giá Năng Lực (ĐGNL) là một bước quan trọng trong quá trình xét tuyển vào các trường Đại học Quốc gia TP.HCM. Trong số các môn thi, môn Toán học được coi là một trong những môn đòi hỏi sự logic, tư duy và khả năng giải quyết vấn đề. Để giúp các thí sinh chuẩn bị tốt cho kỳ thi ĐGNL, “Đề Thi Đánh Giá Năng Lực 2023 Đại Học Quốc Gia TP.HCM Môn Toán” đã được biên soạn.
“Đề Thi Đánh Giá Năng Lực 2023 Đại Học Quốc Gia TP.HCM Môn Toán” là một bộ đề thi đặc biệt, được thiết kế bởi các giáo viên có kinh nghiệm trong việc giảng dạy môn Toán học và nắm vững định hướng của kỳ thi ĐGNL. Bộ đề này không chỉ cung cấp cho thí sinh những câu hỏi và bài tập đa dạng, mà còn giúp rèn luyện kỹ năng tính toán, tư duy logic và khả năng giải quyết vấn đề.
Tham khảo “Đề Thi Đánh Giá Năng Lực 2023 Đại Học Quốc Gia TP.HCM Môn Toán” mang lại nhiều lợi ích quan trọng cho thí sinh. Đầu tiên, bộ đề này giúp thí sinh làm quen với cấu trúc và yêu cầu của kỳ thi ĐGNL môn Toán học. Các câu hỏi và bài tập trong đề thi được xây dựng dựa trên kiến thức và kỹ năng quan trọng, giúp thí sinh làm quen với các dạng bài và nắm vững kiến thức cần thiết trong môn Toán học.
>> Đề thi tham khảo
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
ĐẠI HỌC QUỐC GIA TP.HCM KÌ THI ĐÁNH GIÁ NĂNG LỰC
|
ĐỀ THI MẪU NĂM 2021 Môn: Toán |
(Đề thi gồm 4 trang) |
Thời gian: 45 phút (Không kể thời gian phát đề) |
Bạn An chọn một số nguyên, nhân số đó với
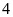 rồi trừ đi
rồi trừ đi
 .
Lấy kết quả có được nhân với
.
Lấy kết quả có được nhân với
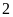 và cuối cùng trừ đi
và cuối cùng trừ đi
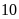 thì được một số có hai chữ số. Số lớn nhất An có
thể chọn có hàng đơn vị bằng
thì được một số có hai chữ số. Số lớn nhất An có
thể chọn có hàng đơn vị bằng
A.
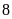 . B.
. B.
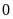 . C.
. C.
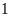 . D.
. D.
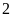 .
.
Một hộp đựng
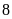 quả cầu xanh,
quả cầu xanh,
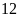 quả cầu đỏ. Lấy ngẫu nhiên
quả cầu đỏ. Lấy ngẫu nhiên
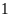 quả cầu trong hộp, sau đó lấy ngẫu nhiên
quả cầu trong hộp, sau đó lấy ngẫu nhiên
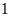 quả cầu trong các quả cầu còn lại. Xác suất để lấy
được
quả cầu trong các quả cầu còn lại. Xác suất để lấy
được
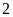 quả
cầu cùng màu là
quả
cầu cùng màu là
A.
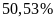 . B.
. B.
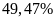 . C.
. C.
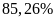 . D.
. D.
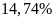 .
.
Hàm số
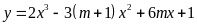 nghịch biến trên khoảng
nghịch biến trên khoảng
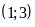 khi và chỉ khi
khi và chỉ khi
A.
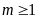 . B.
. B.
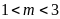 . C.
. C.
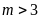 . D.
. D.
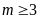 .
.
Gọi
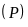 là mặt phẳng chứa điểm
là mặt phẳng chứa điểm
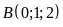 sao cho khoảng cách từ điểm
sao cho khoảng cách từ điểm
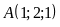 đến
đến
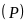 là lớn nhất. Phương trình của
là lớn nhất. Phương trình của
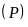 là
là
A.
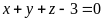 . B.
. B.
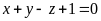 . C.
. C.
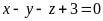 . D.
. D.
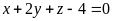 .
.
Đặt
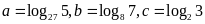 .
Khi đó
.
Khi đó
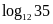 bằng
bằng
A.
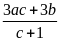 . B.
. B.
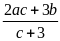 . C.
. C.
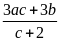 . D.
. D.
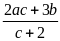 .
.
Lan mua một máy tính xách tay tại một cửa hàng với giá niêm yết đã giảm 20% so với giá ban đầu. Tổng số tiền phải trả là 10 triệu đồng, bao gồm 8% thuế giá trị gia tăng trên giá niêm yết. Giá ban đầu của máy tính trên là
A.
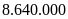 đ. B.
đ. B.
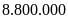 đ. C.
đ. C.
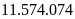 đ. D.
đ. D.
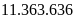 đ.
đ.
Cho hai đường thẳng
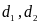 song song với nhau. Trên
song song với nhau. Trên
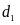 lấy 5 điểm phân biệt, trên
lấy 5 điểm phân biệt, trên
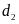 lấ 4 điểm phân biệt. Số tam giác có 3 đỉnh là 3 điểm
có được từ các điểm trên là
lấ 4 điểm phân biệt. Số tam giác có 3 đỉnh là 3 điểm
có được từ các điểm trên là
A. 90. B. 180. C. 140. D. 70.
Cho khối lăng trụ
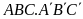 có thể tích bằng 12. Thể tích của khối tứ diện
có thể tích bằng 12. Thể tích của khối tứ diện
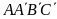
A. 3. B. 6. C. 4. D. 2.
Số nghiệm phức của phương trình
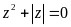 là
là
A. 3. B. 4. C. 2. D. 1.
Một vật chuyển động với vận tốc thay đổi theo thời gian
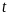 là
là
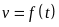
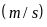 .
Gọi
.
Gọi
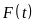 và
và
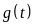 lần lượt là nguyên hàm và đạo hàm của
lần lượt là nguyên hàm và đạo hàm của
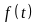 .
Quãng đường vật đi được từ thời điểm
.
Quãng đường vật đi được từ thời điểm
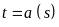 đến thời điểm
đến thời điểm
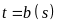 bằng
bằng
A.
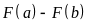 . B.
. B.
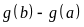 . C.
. C.
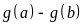 . D.
. D.
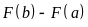 .
.
Một tổ gồm 6 sinh viên (An, Bình, Cường, Danh, Giang, Hoàng) được chia làm 3 cặp làm bài tập thực hành. An làm cùng với Danh; Cường không làm cùng với Giang; Bình không cùng làm với Cường. Hỏi Giang cùng làm với ai?
A. Cường. B. Bình. C. An. D. Hoàng.
Một nhóm 6 người M, N, P, Q, R, S ngồi quanh một bàn tròn. Q ngồi cạnh M và R; P ngồi cạnh R nhưng không ngồi cạnh S. Vậy N ngồi cạnh hai người nào?
A. M và P. B. R và M. C. M và S. D. S và P.
Dựa vào thông tin dưới đây để trả lời các câu từ 53 đến 56
Trong
một cuộc thi Olympic, năm giải thưởng cao nhất được
trao cho các học sinh
 .
Dưới đây là các thông tin của buổi trao giải:
.
Dưới đây là các thông tin của buổi trao giải:
-
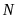 hoặc
hoặc
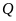 đạt giải tư.
đạt giải tư.
-
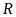 đạt giải cao hơn
đạt giải cao hơn
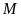 .
.
-
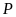 không đạt giải ba.
không đạt giải ba.
Danh sách nào dưới đây có thể là thứ tự các học sinh đạt giải, từ giải nhất đến giải năm?
A.
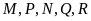 . B.
. B.
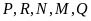 . C.
. C.
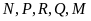 . D.
. D.
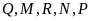 .
.
Nếu
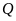 đạt giải năm thì
đạt giải năm thì
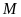 sẽ đạt giải nào?
sẽ đạt giải nào?
A. nhất. B. nhì. C. ba. D. tư.
Nếu
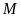 đạt giải nhì thì phát biểu nào sau đây có
thể
sai?
đạt giải nhì thì phát biểu nào sau đây có
thể
sai?
A.
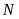 không đạt giải ba. B.
không đạt giải ba. B.
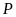 không đạt giải nhất.
không đạt giải nhất.
C.
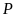 không đạt giải tư. D.
không đạt giải tư. D.
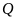 không đạt giải nhất.
không đạt giải nhất.
Nếu
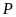 đạt giải cao hơn
đạt giải cao hơn
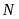 đúng
đúng
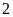 bậc thì phát biểu nào sau đây nêu đầy đủ và chính
xác danh sách các học sinh có
thể đạt
giải nhì?
bậc thì phát biểu nào sau đây nêu đầy đủ và chính
xác danh sách các học sinh có
thể đạt
giải nhì?
A.
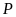 . B.
. B.
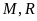 . C.
. C.
 . D.
. D.
 .
.
Dựa vào thông tin dưới đây để trả lời các câu từ 57 đến 60
Có 7 học sinh được xếp ngồi vào 7 ghế trong một hàng từ trái sang phải. Trong đó có 4 học sinh nam là M, N, P, Q và 3 học sinh nữ là X, Y, Z. Chỗ ngồi của học sinh được xếp theo các nguyên tắc:
- Mỗi ghế chỉ có 1 học sinh ngồi;
- Các học sinh nam không ngồi cạnh nhau;
- P ngồi ở ghế thứ năm (từ trái qua phải);
- Y ngồi phía bên phải P;
- M ngồi cạnh X.
M và X (theo thứ tự) không thể ngồi ở vị trí nào sau đây?
A. thứ nhất và thứ hai. B. thứ hai và thứ ba.
C. thứ ba và thứ tư. D. thứ ba và thứ hai.
Phát biểu nào sau đây sai?
A. N và Q ngồi bên phải M. B. N và X ngồi bên phải M.
C. N và Q ngồi bên trái M. D. Q và X ngồi bên phải M.
Nếu Z ngồi cạnh P và M thì phát biểu nào sau đây có thể sai?
A. M và P ngồi bên phải X. B. M và Y ngồi bên phải X.
C. M và Z ngồi bên trái Y. D. M và X ngồi bên phải Q.
Nếu không có học sinh nữ nào ngồi cạnh cả M và P thì phát biểu nào sau đây có thể đúng?
A. Q ngồi bên trái P. B. X ngồi bên trái M.
C. Z ngồi bên trái M. D. Z ngồi bên trái X.
Dựa vào thông tin dưới đây để trả lời các câu từ 61 đến 63
Biểu đồ bên dưới thể hiện tỷ lệ phần trăm chi phí trong một năm của một công ty.
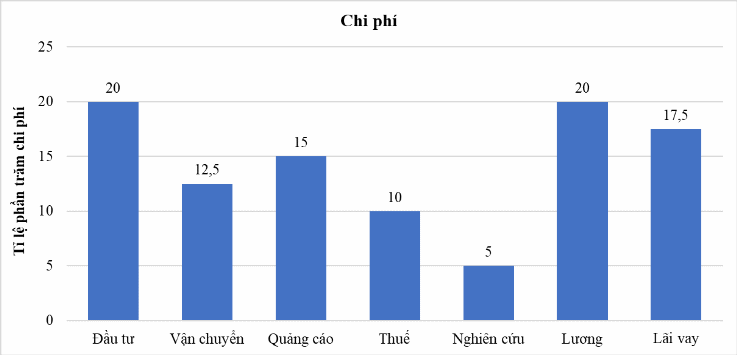
Tổng chi của công ty gấp bao nhiêu lần so với chi cho Nghiên cứu?
A.
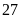 . B.
. B.
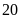 . C.
. C.
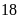 . D.
. D.
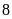 .
.
Nếu chi cho Quảng cáo là
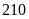 triệu đồng thì chênh lệch giữa chi cho Vận chuyển và
chi cho Thuế là bao nhiêu triệu đồng?
triệu đồng thì chênh lệch giữa chi cho Vận chuyển và
chi cho Thuế là bao nhiêu triệu đồng?
A.
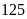 . B.
. B.
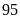 . C.
. C.
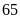 . D.
. D.
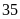 .
.
Nếu chi cho Lãi vay là
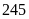 triệu đồng thì tổng chi cho Quảng cáo, Thuế và Nghiên
cứu là bao nhiêu triệu đồng?
triệu đồng thì tổng chi cho Quảng cáo, Thuế và Nghiên
cứu là bao nhiêu triệu đồng?
A.
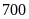 . B.
. B.
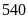 . C.
. C.
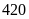 . D.
. D.
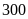 .
.
Dựa vào thông tin dưới đây để trả lời các câu từ 64 đến 67.
Bảng số liệu cung cấp giá vé xe buýt giữa các địa điểm.

Trong các tuyến sau đây, tuyến nào có giá vé thấp nhất?
A. Tuyến I-V. B. Tuyến II-IV. C. Tuyến IV-V. D. Tuyến II-III.
Hành khách từ địa điểm III đi đến địa điểm nào có giá vé thấp nhất?
A. I. B. II. C. IV. D. V.
Một du khách đi từ địa điểm I đến địa điểm IV và muốn dừng lại ở hai địa điểm nữa để tham quan. Lộ trình nào sẽ có giá vé thấp nhất cho du khách?
A. I-II-III-IV. B. I-III-II-IV. C. I-V-III-IV. D. I-III-V-IV.
Do giá nguyên liệu tăng nên giá xe buýt được điều chỉnh tăng thêm 1.000đ cho các tuyến có giá dưới 10.000đ. Nếu số vé được bán ra cho tuyến I-III gấp đôi số vé được bán ra cho tuyến II-III thì tổng doanh thu từ hai tuyến này tăng thêm bao nhiêu phần trăm? Biết rằng số vé được bán ra ở mỗi tuyến là không đổi so với trước khi tăng giá.
A.
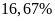 . B.
. B.
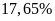 . C.
. C.
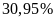 . D.
. D.
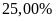 .
.
Dựa vào thông tin dưới đây để trả lời các câu từ 68 đến 70
Tập đoàn
 có 6 công ty A, B, C, D, E, F. Trong năm
có 6 công ty A, B, C, D, E, F. Trong năm
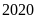 ,
tỷ lệ doanh thu của các công ty này được biểu thị
như hình biểu đồ :
,
tỷ lệ doanh thu của các công ty này được biểu thị
như hình biểu đồ :
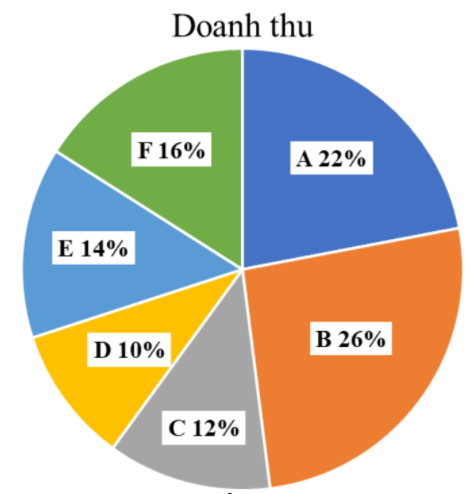
Nếu doanh thu của công ty D là
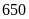 tỷ đồng thì doanh thu của công ty B là bao nhiêu tỷ
đồng?
tỷ đồng thì doanh thu của công ty B là bao nhiêu tỷ
đồng?
A.
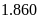 . B.
. B.
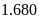 . C.
. C.
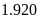 . D.
. D.
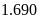 .
.
Doanh thu của công ty F nhiều hơn doanh thu của công ty D là bao nhiêu phần trăm?
A.
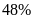 . B.
. B.
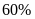 . C.
. C.
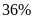 . D.
. D.
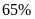 .
.
Nếu doanh thu của công ty E tăng
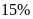 vào năm
vào năm
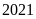 và doanh thu của các công ty khác không thay đổi thì tổng
doanh thu của tập đoàn X tăng bao nhiêu phần trăm?
và doanh thu của các công ty khác không thay đổi thì tổng
doanh thu của tập đoàn X tăng bao nhiêu phần trăm?
A.
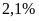 . B.
. B.
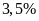 . C.
. C.
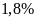 . D.
. D.
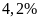 .
.
HẾT
ĐẠI HỌC QUỐC GIA TP.HCM KÌ THI ĐÁNH GIÁ NĂNG LỰC
|
ĐỀ THI MẪU NĂM 2021 Môn: Toán |
|
Thời gian: 45 phút (Không kể thời gian phát đề) |
BẢNG ĐÁP ÁN
41.C |
42.B |
43.D |
44.B |
45.C |
46.C |
47.D |
48.C |
49.A |
50.D |
51.B |
52.D |
53.C |
54.C |
55.A |
56.C |
57.B |
58.C |
59.D |
60.A |
61.B |
62.D |
63.C |
64.D |
65.A |
66.D |
67.B |
68.D |
69.B |
70.A |
HƯỚNG DẪN GIẢI CHI TIẾT
Bạn An chọn một số nguyên, nhân số đó với
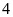 rồi trừ đi
rồi trừ đi
 .
Lấy kết quả có được nhân với
.
Lấy kết quả có được nhân với
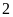 và cuối cùng trừ đi
và cuối cùng trừ đi
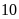 thì được một số có hai chữ số. Số lớn nhất An có
thể chọn có hàng đơn vị bằng
thì được một số có hai chữ số. Số lớn nhất An có
thể chọn có hàng đơn vị bằng
A.
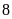 . B.
. B.
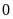 . C.
. C.
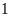 . D.
. D.
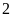 .
.
Lời giải
Chọn C
Gọi
số lớn nhất An có thể chọn là
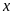 (
(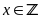 ),
số nhận được sau khi An thực hiện các phép toán là
),
số nhận được sau khi An thực hiện các phép toán là
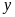 (
(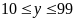 hoặc
hoặc
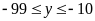 ;
;
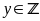 )
)
Ta
có:
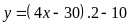
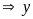 là số chẵn
là số chẵn
Do
đó:
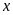 lớn nhất
lớn nhất
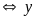 lớn nhất
lớn nhất
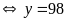
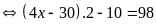
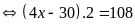
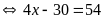
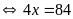
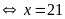
Vậy
số lớn nhất An có thể chọn có hàng đơn vị bằng
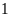 .
.
Một hộp đựng
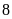 quả cầu xanh,
quả cầu xanh,
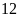 quả cầu đỏ. Lấy ngẫu nhiên
quả cầu đỏ. Lấy ngẫu nhiên
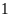 quả cầu trong hộp, sau đó lấy ngẫu nhiên
quả cầu trong hộp, sau đó lấy ngẫu nhiên
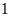 quả cầu trong các quả cầu còn lại. Xác suất để lấy
được
quả cầu trong các quả cầu còn lại. Xác suất để lấy
được
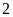 quả
cầu cùng màu là
quả
cầu cùng màu là
A.
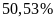 . B.
. B.
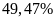 . C.
. C.
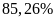 . D.
. D.
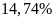 .
.
Lời giải
Chọn B
Không
gian mẫu là lấy
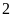 quả cầu trong hộp một cách lần lượt, ngẫu nhiên nên
số phần tử của không gian mẫu là
quả cầu trong hộp một cách lần lượt, ngẫu nhiên nên
số phần tử của không gian mẫu là
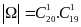 .
.
Gọi
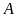 là biến cố “
là biến cố “ quả cầu lấy được cùng màu”. Ta có các trường hợp
thuận lợi cho biến cố
quả cầu lấy được cùng màu”. Ta có các trường hợp
thuận lợi cho biến cố
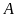 như sau:
như sau:
 TH1:
Lần thứ nhất lấy quả cầu màu xanh và lần thứ hai
cũng lấy quả cầu màu xanh:
TH1:
Lần thứ nhất lấy quả cầu màu xanh và lần thứ hai
cũng lấy quả cầu màu xanh:
Trường
hợp này có
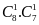 cách.
cách.
 TH2:
Lần thứ nhất lấy quả cầu màu đỏ và lần thứ hai
cũng lấy quả cầu màu đỏ:
TH2:
Lần thứ nhất lấy quả cầu màu đỏ và lần thứ hai
cũng lấy quả cầu màu đỏ:
Trường
hợp này có
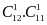 cách.
cách.
Do
đó, số phần tử của biến cố
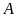 là
là
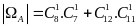 .
.
Vậy
xác suất cần tính là
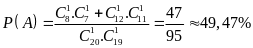 .
.
Hàm số
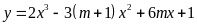 nghịch biến trên khoảng
nghịch biến trên khoảng
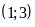 khi và chỉ khi
khi và chỉ khi
A.
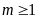 . B.
. B.
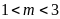 . C.
. C.
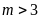 . D.
. D.
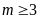 .
.
Lời giải
Chọn D
Hàm
số
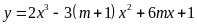
Tập
xác định:
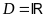
Ta
có:
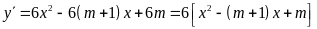
Hàm
số nghịch biến trên
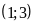
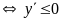 với
với
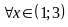
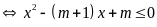 với
với
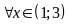
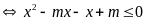 với
với
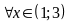
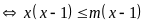 với
với
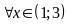
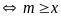 với
với
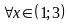
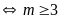
Vậy
với
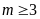 thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng
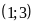 .
.
Gọi
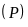 là mặt phẳng chứa điểm
là mặt phẳng chứa điểm
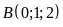 sao cho khoảng cách từ điểm
sao cho khoảng cách từ điểm
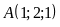 đến
đến
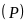 là lớn nhất. Phương trình của
là lớn nhất. Phương trình của
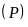 là
là
A.
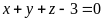 . B.
. B.
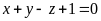 . C.
. C.
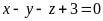 . D.
. D.
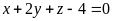 .
.
Lời giải
Chọn B
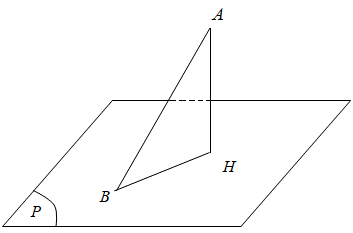
Gọi
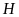 là hình chiếu của
là hình chiếu của
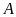 trên mặt phẳng
trên mặt phẳng
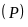 .
.
Ta
có:
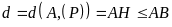 .
.
Dấu
“=” xảy ra khi và chỉ khi
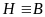 .
.
Do
đó
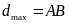 khi
khi
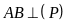 .
.
Khi
đó, mặt phẳng
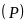 đi qua
đi qua
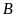 và nhận
và nhận
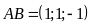 làm vectơ pháp tuyến nên có phương trình là:
làm vectơ pháp tuyến nên có phương trình là:
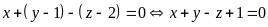 .
.
Đặt
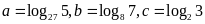 .
Khi đó
.
Khi đó
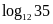 bằng
bằng
A.
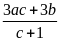 . B.
. B.
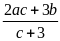 . C.
. C.
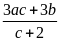 . D.
. D.
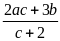 .
.
Lời giải
Chọn C
Từ giả thiết ta có:
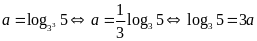 ;
;
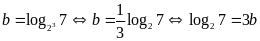 .
.
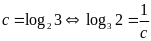 .
.
Khi
đó
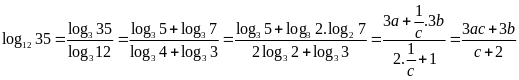 .
.
Lan mua một máy tính xách tay tại một cửa hàng với giá niêm yết đã giảm 20% so với giá ban đầu. Tổng số tiền phải trả là 10 triệu đồng, bao gồm 8% thuế giá trị gia tăng trên giá niêm yết. Giá ban đầu của máy tính trên là
A.
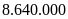 đ. B.
đ. B.
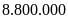 đ. C.
đ. C.
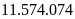 đ. D.
đ. D.
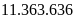 đ.
đ.
Lời giải
Chọn C
Giả
sử máy tính có giá niêm yết là
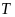 ,
giá ban đầu là
,
giá ban đầu là
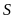 .
.
Ta
có:
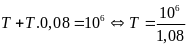 .
.
Khi
đó giá ban đầu của máy tính là:
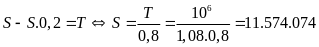 đ.
đ.
Cho hai đường thẳng
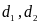 song song với nhau. Trên
song song với nhau. Trên
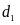 lấy 5 điểm phân biệt, trên
lấy 5 điểm phân biệt, trên
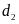 lấ 4 điểm phân biệt. Số tam giác có 3 đỉnh là 3 điểm
có được từ các điểm trên là
lấ 4 điểm phân biệt. Số tam giác có 3 đỉnh là 3 điểm
có được từ các điểm trên là
A. 90. B. 180. C. 140. D. 70.
Lời giải
Chọn D
Để
chọn được 3 điểm là 3 đỉnh của một tam giác, cần
chọn 2 điểm thuộc đường thẳng này và 1 điểm còn
lại thuộc đường thẳng kia. Do đó số tam giác có 3
đỉnh là 3 điểm có được từ các điểm trên là:
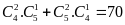 .
.
Cho khối lăng trụ
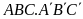 có thể tích bằng 12. Thể tích của khối tứ diện
có thể tích bằng 12. Thể tích của khối tứ diện
A. 3. B. 6. C. 4. D. 2.
Lời giải
Chọn C
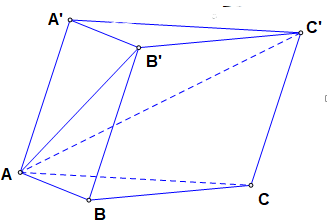
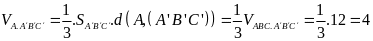
Số nghiệm phức của phương trình
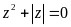 là
là
A. 3. B. 4. C. 2. D. 1.
Lời giải
Chọn A
Đặt
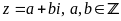 .
Ta có:
.
Ta có:
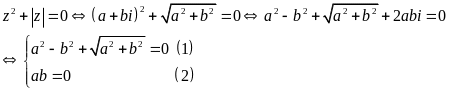
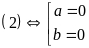
+)
Với
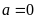 thay vào (1) ta được
thay vào (1) ta được
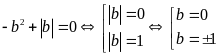 .
.
Suy
ra
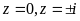 .
.
+)
Với
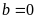 thay vào (1) ta được
thay vào (1) ta được
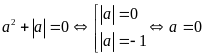 .
.
Vậy
phương trình đã cho có 3 nghiệm
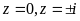 .
.
Một vật chuyển động với vận tốc thay đổi theo thời gian
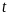 là
là
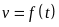
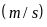 .
Gọi
.
Gọi
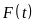 và
và
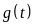 lần lượt là nguyên hàm và đạo hàm của
lần lượt là nguyên hàm và đạo hàm của
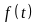 .
Quãng đường vật đi được từ thời điểm
.
Quãng đường vật đi được từ thời điểm
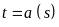 đến thời điểm
đến thời điểm
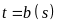 bằng
bằng
A.
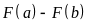 . B.
. B.
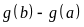 . C.
. C.
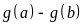 . D.
. D.
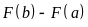 .
.
Lời giải
Chọn D
Quãng
đường vật đi được từ thời điểm
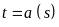 đến thời điểm
đến thời điểm
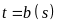 là
là
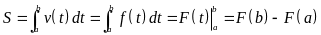 .
.
Một tổ gồm 6 sinh viên (An, Bình, Cường, Danh, Giang, Hoàng) được chia làm 3 cặp làm bài tập thực hành. An làm cùng với Danh; Cường không làm cùng với Giang; Bình không cùng làm với Cường. Hỏi Giang cùng làm với ai?
A. Cường. B. Bình. C. An. D. Hoàng.
Lời giải
Chọn B
Vì An làm cùng với Danh nên ta không xét hai bạn này nữa.
Vì Cường không làm cùng với Giang nên Cường chỉ có làm cùng với Bình và Hoàng nhưng mà Bình không cùng làm với Cường nên từ đó suy ra Cường chỉ có thể làm với Hoàng nên Bình và Giang sẽ làm chung với nhau.
Một nhóm 6 người M, N, P, Q, R, S ngồi quanh một bàn tròn. Q ngồi cạnh M và R; P ngồi cạnh R nhưng không ngồi cạnh S. Vậy N ngồi cạnh hai người nào?
A. M và P. B. R và M. C. M và S. D. S và P.
Lời giải
Chọn D
Vì Q ngồi cạnh M và R; P ngồi cạnh R nhưng không ngồi cạnh S nên ta có sơ đồ chỗ ngồi sau
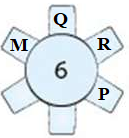
Khi đó, bắt buộc S phải ngồi cạnh M và chỗ cuối cùng phải dành cho N.
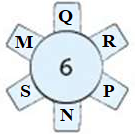
Vậy N ngồi cạnh hai người S và P.
Dựa vào thông tin dưới đây để trả lời các câu từ 53 đến 56
Trong
một cuộc thi Olympic, năm giải thưởng cao nhất được
trao cho các học sinh
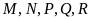 .
Dưới đây là các thông tin của buổi trao giải:
.
Dưới đây là các thông tin của buổi trao giải:
-
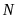 hoặc
hoặc
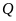 đạt giải tư.
đạt giải tư.
-
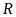 đạt giải cao hơn
đạt giải cao hơn
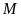 .
.
-
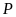 không đạt giải ba.
không đạt giải ba.
Danh sách nào dưới đây có thể là thứ tự các học sinh đạt giải, từ giải nhất đến giải năm?
A.
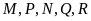 . B.
. B.
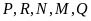 . C.
. C.
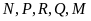 . D.
. D.
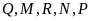 .
.
Lời giải
Chọn C
+
Vì
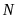 hoặc
hoặc
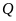 đạt giải tư nên phương án
đạt giải tư nên phương án
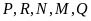 bị loại.
bị loại.
+
Vì
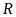 đạt giải cao hơn
đạt giải cao hơn
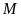 nên các phương án
nên các phương án
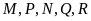 ,
,
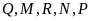 bị loại.
bị loại.
Vậy
phương án có thể xảy ra là
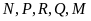 .
.
Nếu
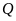 đạt giải năm thì
đạt giải năm thì
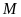 sẽ đạt giải nào?
sẽ đạt giải nào?
A. nhất. B. nhì. C. ba. D. tư.
Lời giải
Chọn C
+
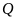 đạt giải năm thì
đạt giải năm thì
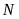 đạt giải tư.
đạt giải tư.
+
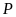 không đạt giải ba nên giải ba chỉ có thể là
không đạt giải ba nên giải ba chỉ có thể là
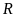 hoặc
hoặc
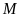 .
.
+
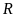 đạt giải cao hơn
đạt giải cao hơn
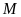 nên
nên
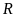 không thể đạt giải ba.
không thể đạt giải ba.
Vậy
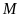 đạt giải ba.
đạt giải ba.
Nếu
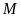 đạt giải nhì thì phát biểu nào sau đây có
thể
sai?
đạt giải nhì thì phát biểu nào sau đây có
thể
sai?
A.
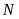 không đạt giải ba. B.
không đạt giải ba. B.
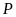 không đạt giải nhất.
không đạt giải nhất.
C.
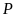 không đạt giải tư. D.
không đạt giải tư. D.
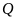 không đạt giải nhất.
không đạt giải nhất.
Lời giải
Chọn A
+
Vì
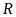 đạt giải cao hơn
đạt giải cao hơn
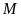 nên khi
nên khi
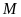 đạt giải nhì thì
đạt giải nhì thì
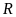 đạt giải nhất, do đó các phương án “
đạt giải nhất, do đó các phương án “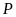 không đạt giải nhất” và “
không đạt giải nhất” và “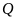 không đạt giải nhất” là đúng.
không đạt giải nhất” là đúng.
+
Vì
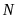 hoặc
hoặc
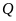 đạt giải tư nên phương án “
đạt giải tư nên phương án “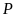 không đạt giải tư” là đúng.
không đạt giải tư” là đúng.
Vậy
phương án có thể sai là “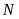 không đạt giải ba”.
không đạt giải ba”.
Nếu
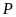 đạt giải cao hơn
đạt giải cao hơn
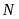 đúng
đúng
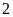 bậc thì phát biểu nào sau đây nêu đầy đủ và chính
xác danh sách các học sinh có
thể đạt
giải nhì?
bậc thì phát biểu nào sau đây nêu đầy đủ và chính
xác danh sách các học sinh có
thể đạt
giải nhì?
A.
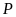 . B.
. B.
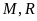 . C.
. C.
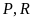 . D.
. D.
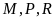 .
.
Lời giải
Chọn C
Xét hai trường hợp:
- Trường hợp
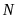 đạt giải tư.
đạt giải tư.
Khi đó
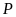 đạt giải nhì. Một thứ tự các học sinh đạt giải,
từ giải nhất đến giải năm, có thể xảy ra thỏa mãn
bài toán là
đạt giải nhì. Một thứ tự các học sinh đạt giải,
từ giải nhất đến giải năm, có thể xảy ra thỏa mãn
bài toán là
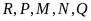 .
.
Suy ra
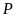 có thể đạt giải nhì.
có thể đạt giải nhì.
- Trường hợp
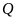 đạt giải tư. Hiển nhiên
đạt giải tư. Hiển nhiên
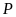 không đạt giải năm.
không đạt giải năm.
Vì
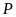 không đạt giải ba nên
không đạt giải ba nên
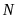 không đạt giải năm. Đồng thời
không đạt giải năm. Đồng thời
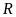 đạt giải cao hơn
đạt giải cao hơn
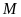 nên
nên
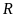 không đạt giải năm. Do đó
không đạt giải năm. Do đó
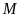 đạt giải năm.
đạt giải năm.
Vì
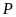 đạt giải cao hơn
đạt giải cao hơn
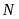 đúng
đúng
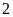 bậc nên các học sinh
bậc nên các học sinh
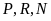 tương ứng đạt các giải nhất, nhì ba.
tương ứng đạt các giải nhất, nhì ba.
Suy ra
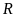 có thể đạt giải nhì.
có thể đạt giải nhì.
Vậy danh sách đầy đủ và chính xác các
học sinh có thể đạt giải nhì là
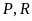 .
.
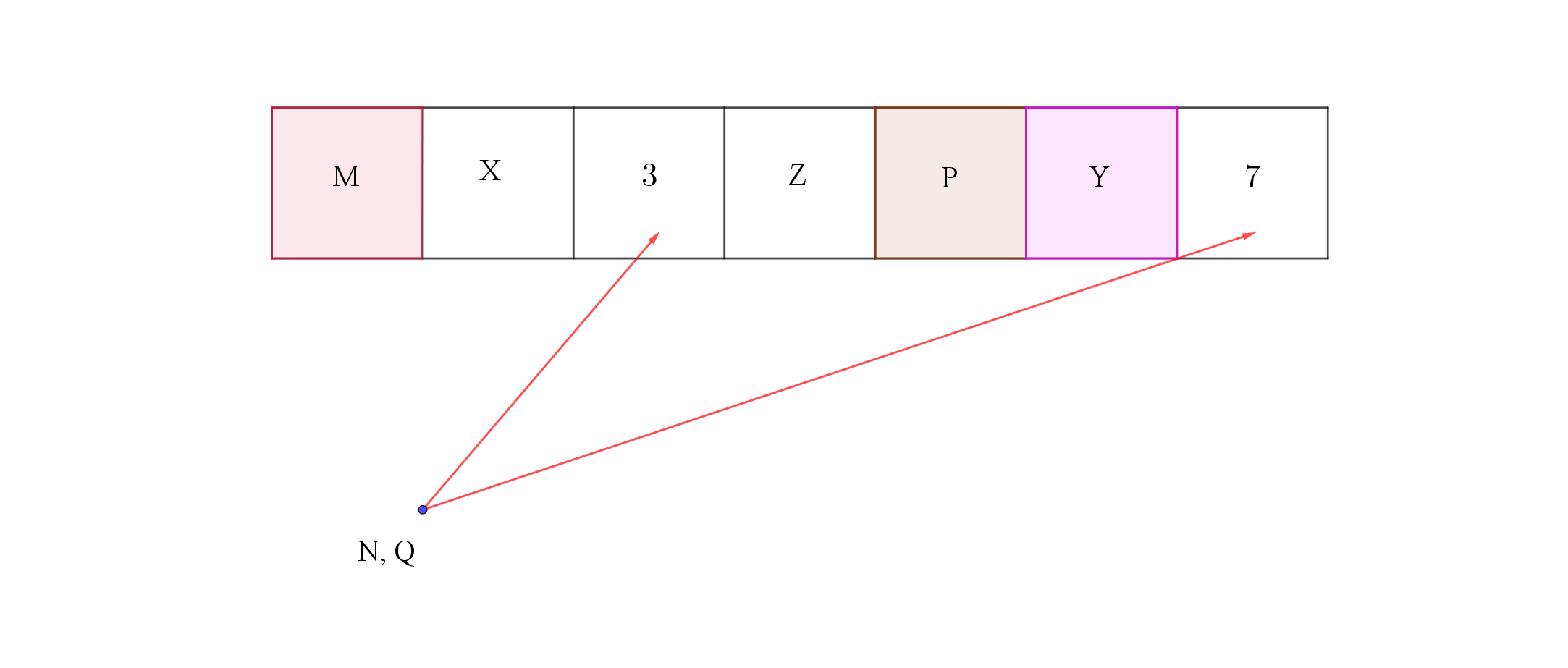
Dựa vào thông tin dưới đây để trả lời các câu từ 57 đến 60
Có 7 học sinh được xếp ngồi vào 7 ghế trong một hàng từ trái sang phải. Trong đó có 4 học sinh nam là M, N, P, Q và 3 học sinh nữ là X, Y, Z. Chỗ ngồi của học sinh được xếp theo các nguyên tắc:
- Mỗi ghế chỉ có 1 học sinh ngồi;
- Các học sinh nam không ngồi cạnh nhau;
- P ngồi ở ghế thứ năm (từ trái qua phải);
- Y ngồi phía bên phải P;
- M ngồi cạnh X.
Ta có hình vẽ minh họa sau:
M và X (theo thứ tự) không thể ngồi ở vị trí nào sau đây?
A. thứ nhất và thứ hai. B. thứ hai và thứ ba.
C. thứ ba và thứ tư. D. thứ ba và thứ hai.
Lời giải
Chọn B
Theo giả thiết ta có được hình vẽ minh họa phía trên.
Nhận xét vì nam không ngồi cạnh nhau, lại có 4 nam, 3 nữ nên ta thấy nam nữ phải ngồi xen kẽ, nam ở vị trí lẻ. Lúc này M không thể ngồi ở vị trí thứ hai, thứ sáu được.
Chọn B, D.
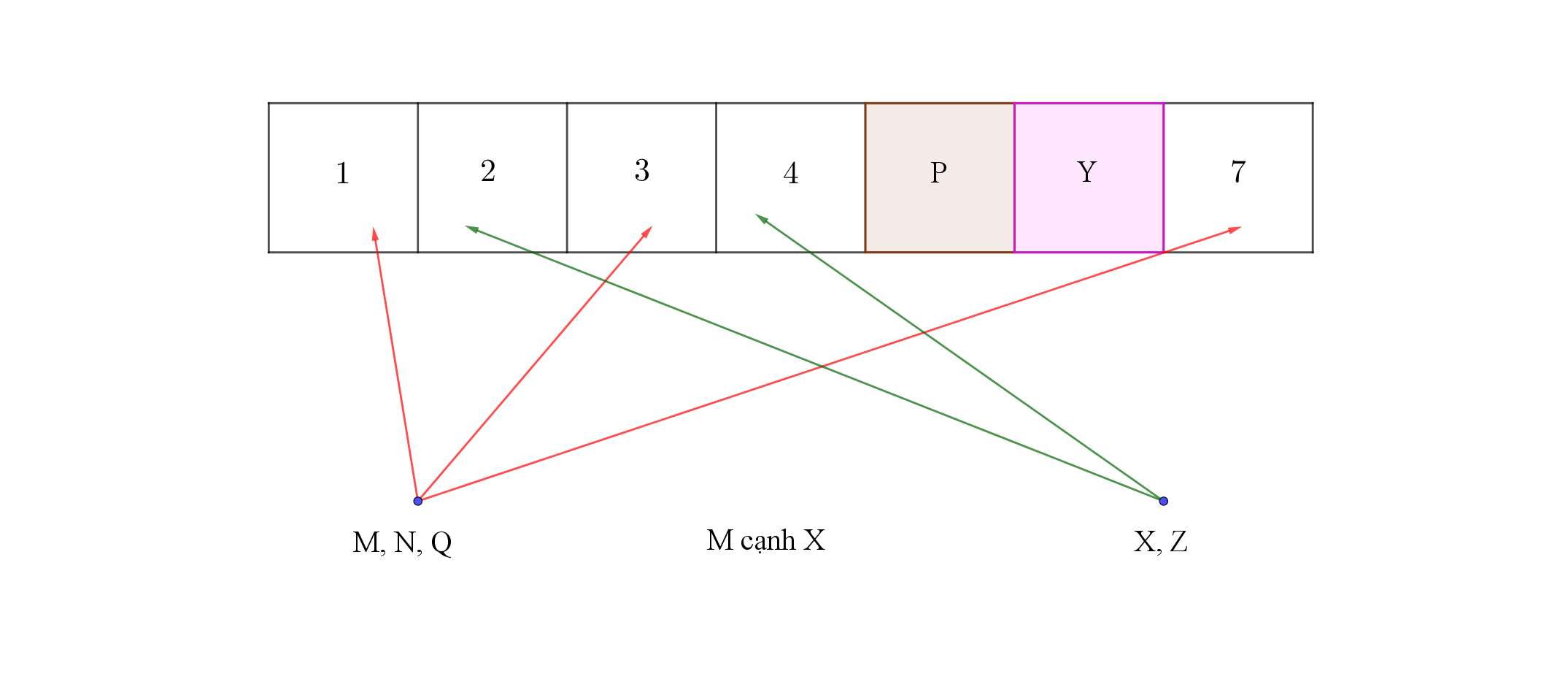
Phát biểu nào sau đây sai?
A. N và Q ngồi bên phải M. B. N và X ngồi bên phải M.
C. N và Q ngồi bên trái M. D. Q và X ngồi bên phải M.
Lời giải
Chọn C
Xét trường hợp M ở vị trí thứ nhất
Nhận xét N và Q không thể ngồi bên trái M. Câu C sai.
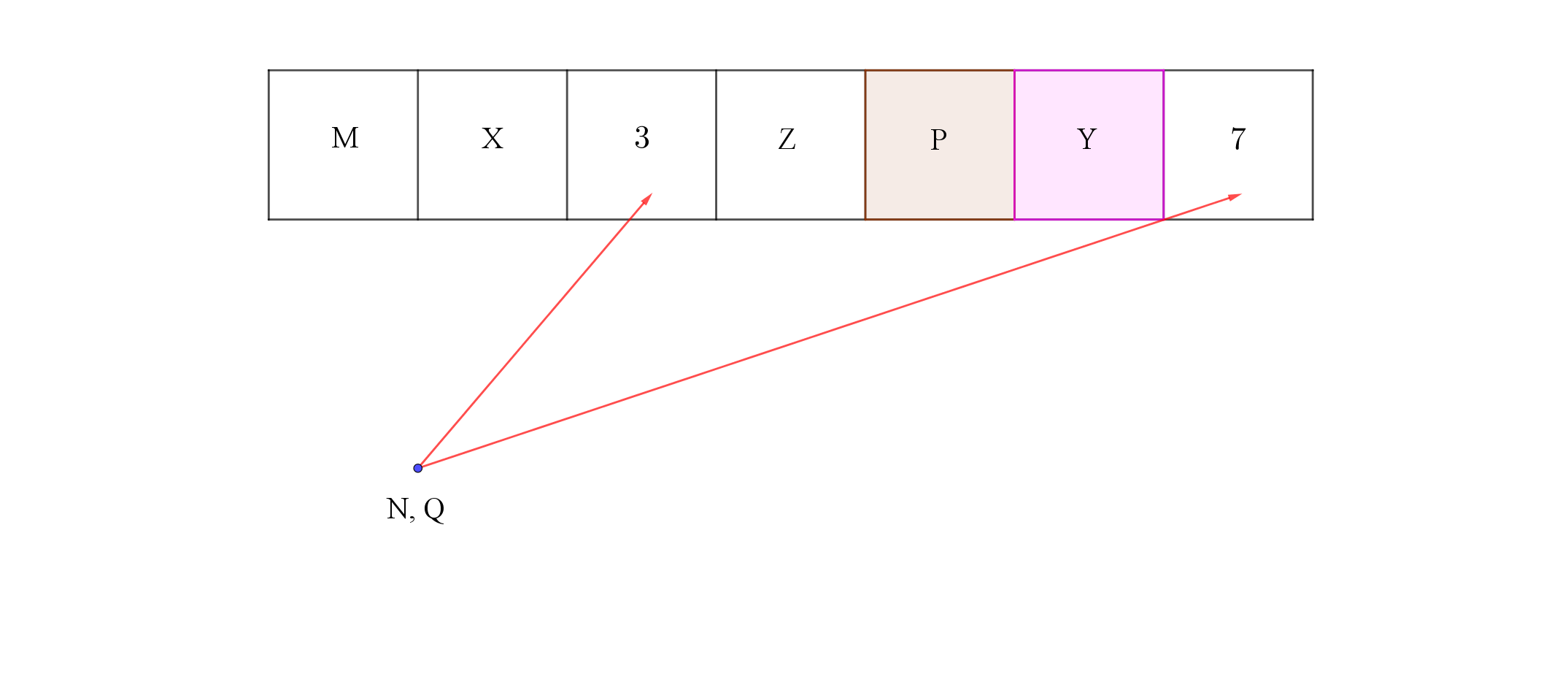
Nếu Z ngồi cạnh P và M thì phát biểu nào sau đây có thể sai?
A. M và P ngồi bên phải X. B. M và Y ngồi bên phải X.
C. M và Z ngồi bên trái Y. D. M và X ngồi bên phải Q.
Lời giải
Chọn D
Theo đề ta có hình vẽ sau:
Với trường hợp Q ngồi ở ví trí thứ 7 thì M và X không thể ngồi bên trái Q nên câu D có thể sai.
Nếu không có học sinh nữ nào ngồi cạnh cả M và P thì phát biểu nào sau đây có thể đúng?
A. Q ngồi bên trái P. B. X ngồi bên trái M.
C. Z ngồi bên trái M. D. Z ngồi bên trái X.
Lời giải
Chọn A
Nhận xét: Với giả thiết “không có học sinh nữ nào ngồi cạnh cả M và P” nghĩa là M và P không thể ở hai vị trí lẻ liên tiếp hay nghĩa là có 2 bạn nữ ngồi giữa M và P.
Mà P ở vị trí cố định thứ năm nên suy ra M chỉ có thể ở vị trí thứ nhất. Loại câu B, C.
M luôn ngồi cạnh X nên X ở vị trí thứ hai nên Z không thể ngồi bên trái X. Loại câu D.
Q có thể ở 2 vị trí lẻ còn lại là thứ ba hoặc thứ năm. Suy ra Q có thể ngồi bên trái P (vị trí thứ ba).
Chọn A.
Dựa vào thông tin dưới đây để trả lời các câu từ 61 đến 63
Biểu đồ bên dưới thể hiện tỷ lệ phần trăm chi phí trong một năm của một công ty.

Tổng chi của công ty gấp bao nhiêu lần so với chi cho Nghiên cứu?
A.
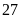 . B.
. B.
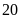 . C.
. C.
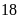 . D.
. D.
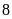 .
.
Lời giải
Chọn B
Bởi vì tổng chi phí tương đương 100%.
Tỉ lệ phần trăm chi phí cho Nghiên cứu là 5%.
Vậy tổng chi phí gấp 100/5=20 lần chi phí cho nghiên cứu.
Nếu chi cho Quảng cáo là
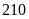 triệu đồng thì chênh lệch giữa chi cho Vận chuyển và
chi cho Thuế là bao nhiêu triệu đồng?
triệu đồng thì chênh lệch giữa chi cho Vận chuyển và
chi cho Thuế là bao nhiêu triệu đồng?
A.
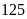 . B.
. B.
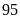 . C.
. C.
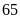 . D.
. D.
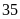 .
.
Lời giải
Chọn D
Ta
có: Chi phí Quảng cáo là
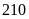 triệu đồng.
triệu đồng.
Bên
cạnh đó, chi phí Quảng cáo chiếm
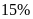 tổng chi phí.
tổng chi phí.
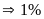 tương
đương
tương
đương
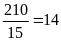 triệu đồng.
triệu đồng.
Chênh
lệch giữa chi phí Vận chuyển và thuế là
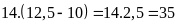 (triệu
đồng).
(triệu
đồng).
Lưu ý: Khi gặp câu hỏi về số tiền, số lượng mà đề cho số liệu phần trăm ta cần quy đổi phần trăm về số liệu và tiến hành tính toán.
Nếu chi cho Lãi vay là
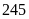 triệu đồng thì tổng chi cho Quảng cáo, Thuế và Nghiên
cứu là bao nhiêu triệu đồng?
triệu đồng thì tổng chi cho Quảng cáo, Thuế và Nghiên
cứu là bao nhiêu triệu đồng?
A.
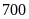 . B.
. B.
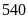 . C.
. C.
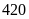 . D.
. D.
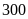 .
.
Lời giải
Chọn C
Ta
có: Chi phí Lãi vay là
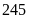 triệu đồng.
triệu đồng.
Bên
cạnh đó, chi phí Lãi vay chiếm
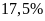 tổng chi phí.
tổng chi phí.
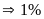 tương
đương
tương
đương
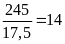 triệu đồng.
triệu đồng.
Tổng
chi phí cho Quảng cáo, Thuế, Nghiên cứu là
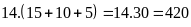 (triệu đồng).
(triệu đồng).
Lưu ý: Khi gặp câu hỏi về số tiền, số lượng mà đề cho số liệu phần trăm ta cần quy đổi phần trăm về số liệu và tiến hành tính toán.
Dựa vào thông tin dưới đây để trả lời các câu từ 64 đến 67.
Bảng số liệu cung cấp giá vé xe buýt giữa các địa điểm.

Trong các tuyến sau đây, tuyến nào có giá vé thấp nhất?
A. Tuyến I-V. B. Tuyến II-IV. C. Tuyến IV-V. D. Tuyến II-III.
Lời giải
Chọn D
Dựa vào bảng số liệu ta thấy:
+ Tuyến I-V có giá vé là 10.000đ
+ Tuyến II-IV có giá vé là 25.000đ
+ Tuyến IV-V có giá vé là 10.000đ
+ Tuyến II-III có giá vé là 7.000đ
Do đó tuyến có giá vé thấp nhất trong 4 tuyến là II-III.
Hành khách từ địa điểm III đi đến địa điểm nào có giá vé thấp nhất?
A. I. B. II. C. IV. D. V.
Lời giải
Chọn A
Dựa vào bảng số liệu ta thấy:
+ Tuyến III-I có giá vé là 5.000đ
+ Tuyến III-II có giá vé là 7.000đ
+ Tuyến III-IV có giá vé là 20.000đ
+ Tuyến III-V có giá vé là 15.000đ
Do đó tuyến có giá vé thấp nhất trong 4 tuyến trên là III-I.
Một du khách đi từ địa điểm I đến địa điểm IV và muốn dừng lại ở hai địa điểm nữa để tham quan. Lộ trình nào sẽ có giá vé thấp nhất cho du khách?
A. I-II-III-IV. B. I-III-II-IV. C. I-V-III-IV. D. I-III-V-IV.
Lời giải
Chọn D
Lộ
trình I-II-III-IV có tổng số tiền vé là
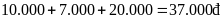 .
.
Lộ
trình I-III-II-IV có tổng số tiền vé là
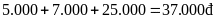 .
.
Lộ
trình I-V-III-IV có tổng số tiền vé là
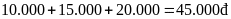 .
.
Lộ
trình I-III-V-IV có tổng số tiền vé là
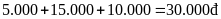 .
.
Do giá nguyên liệu tăng nên giá xe buýt được điều chỉnh tăng thêm 1.000đ cho các tuyến có giá dưới 10.000đ. Nếu số vé được bán ra cho tuyến I-III gấp đôi số vé được bán ra cho tuyến II-III thì tổng doanh thu từ hai tuyến này tăng thêm bao nhiêu phần trăm? Biết rằng số vé được bán ra ở mỗi tuyến là không đổi so với trước khi tăng giá.
A.
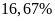 . B.
. B.
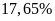 . C.
. C.
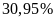 . D.
. D.
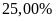 .
.
Lời giải
Chọn B
Gọi
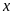 là
số vé bán ra của tuyến II-III,
là
số vé bán ra của tuyến II-III,
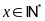 .
Suy ra doanh thu của tuyến II-III là
.
Suy ra doanh thu của tuyến II-III là
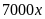 (đồng).
(đồng).
Suy
ra số vé bán ra của tuyến I-III là
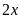 .
Suy ra doanh thu của tuyến I-III là
.
Suy ra doanh thu của tuyến I-III là
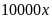 (đồng).
(đồng).
Do
giá vé tuyến II-III và I-III tăng thêm 1.000đ và số vé
bán không đổi nên doanh thu của 2 tuyến sau khi tăng giá
lần lượt là
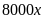 (đồng) và
(đồng) và
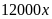 (đồng).
(đồng).
Do
đó tổng doanh thu 2 tuyến tăng thêm là
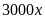 (đồng).
(đồng).
Vậy
tổng doanh thu 2 tuyến tăng thêm
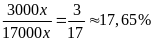 .
.
Dựa vào thông tin dưới đây để trả lời các câu từ 68 đến 70
Tập đoàn
 có 6 công ty A, B, C, D, E, F. Trong năm
có 6 công ty A, B, C, D, E, F. Trong năm
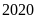 ,
tỷ lệ doanh thu của các công ty này được biểu thị
như hình biểu đồ :
,
tỷ lệ doanh thu của các công ty này được biểu thị
như hình biểu đồ :

Nếu doanh thu của công ty D là
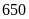 tỷ đồng thì doanh thu của công ty B là bao nhiêu tỷ
đồng?
tỷ đồng thì doanh thu của công ty B là bao nhiêu tỷ
đồng?
A.
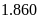 . B.
. B.
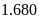 . C.
. C.
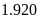 . D.
. D.
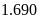 .
.
Lời giải
Chọn D
Doanh thu của toàn bộ doanh nghiệp đó là:
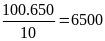 (tỷ đồng)
(tỷ đồng)
Doanh thu của công ty B là:
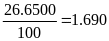 (tỷ đồng)
(tỷ đồng)
Doanh thu của công ty F nhiều hơn doanh thu của công ty D là bao nhiêu phần trăm?
A.
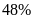 . B.
. B.
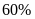 . C.
. C.
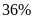 . D.
. D.
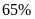 .
.
Lời giải
Chọn B
Mức chênh lệch giữa doanh thu của công ty F và công ty D
là:
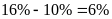
Doanh thu của công ty F nhiều hơn doanh thu của công ty D số
phần trăm là:
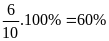
Nếu doanh thu của công ty E tăng
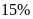 vào năm
vào năm
 và doanh thu của các công ty khác không thay đổi thì tổng
doanh thu của tập đoàn X tăng bao nhiêu phần trăm?
và doanh thu của các công ty khác không thay đổi thì tổng
doanh thu của tập đoàn X tăng bao nhiêu phần trăm?
A.
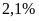 . B.
. B.
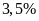 . C.
. C.
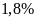 . D.
. D.
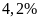 .
.
Lời giải
Chọn A
Không mất tính tổng quát, giả sử doanh thu của toàn bộ tập đoàn X là: 1000 (tỷ đồng)
Khi đó, doanh thu của công ty E là: 140 (tỷ đồng)
Doanh thu của công ty E khi tăng
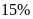 là:
là:
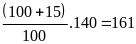 (tỷ đồng)
(tỷ đồng)
Doanh thu của tập đoàn X tăng số
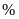 là:
là:
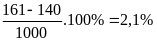
HẾT
Ngoài Đề Thi Đánh Giá Năng Lực 2023 Đại Học Quốc Gia TP.HCM Môn Toán thì các đề thi trong chương trình lớp 12 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
>> Xem thêm






