Phương Pháp Chứng Minh Ba Điểm Thẳng Hàng Có Lời Giải
Có thể bạn quan tâm
| Kế Hoạch Giảng Dạy Môn Địa Lí Lớp 7 |
Phương Pháp Chứng Minh Ba Điểm Thẳng Hàng Có Lời Giải là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
PHƯƠNG PHÁP CHỨNG MINH BA ĐIỂM THẲNG HÀNG
HÌNH HỌC LỚP 7
A. KIẾN THỨC CƠ BẢN:
1. Dựa vào định nghĩa góc bẹt để chứng minh ba điểm thẳng hàng
 A
B C
A
B C
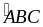 =
1800
=
1800
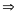 Ba
điểm
A,
B,
C
thẳng
hàng
Ba
điểm
A,
B,
C
thẳng
hàng
2. Vận dụng tiên đề Ơclít chứng minh hai đường thẳng cùng đi qua một điểm và cùng song song với một đường thẳng cho trước



=> A, B, C thẳng hàng
AB // a
AC // a
3. Chứng minh hai đường thẳng cùng đi qua một điểm và cùng vuông góc với

một đường thẳng cho trước:
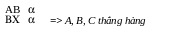
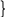

a
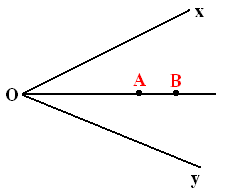
4. Chứng minh ba điểm cùng thuộc tia phân giác của 1 góc
A,
O, B thẳng hàng 

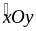
Tia OB
là tia phân giác của

5. Chứng minh ba điểm cùng thuộc đường trung trực của một đoạn thẳng


=> A, B, C thẳng hàng
A thuộc đường trung trực của MN
B thuộc đường trung trực của MN
C thuộc đường trung trực của MN
6. Áp dụng đường trung tuyến của một tam giác thì phải đi qua trọng tâm.
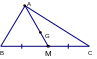
G là trọng tâm tam giác ABC

=> A, G, M thẳng hàng
AM là trung tuyến tam giác ABC

A
7. Chứng minh đường phân giác của tam giác thì đi qua giao điểm chung của chúng:


I
I là
giao
điểm
2
đường
phân
giác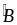 ,
,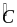
AD
là
phân
giác
của




D
B
C
D thẳng hàng.
8. Chứng minh đường cao của tam giác thì đi qua trực tâm của tam giác đó:
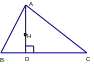
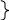
H là trực tâm ABC
AD là đường cao ABC
=> A, H, D thẳng hàng
9. Chứng minh đường trung trực của một cạnh thì đi qua giao điểm hai đường trung trực của hai cạnh còn lại:
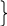
O là giao điểm 2 đường trung trực của 2 cạnh AC và BC
EF là đường trung trực của cạnh AB
=> E, F,O thẳng hàng
10. Sử dụng phương pháp hình duy nhất
Để chứng minh 3 điểm A, B, C thẳng hàng, trong đó C thuộc hình H (hình H là đường thẳng, tia, đoạn thẳng ...) chúng ta có thể gọi C’ là giao điểm của AB với hình H tìm cách chứng minh 2 điểm C và C’ trùng nhau
B. CÁC VÍ DỤ
1. Dựa vào định nghĩa góc bẹt để chứng minh ba điểm thẳng hàng:
 A
B C
A
B C
 =
1800
=
1800
 Ba
điểm
A,
B,
C
thẳng
hàng
Ba
điểm
A,
B,
C
thẳng
hàng
- Ngay từ bài 1: “Hai góc đối đỉnh”, ta có thể lồng vào bài toán yếu tố “3 điểm thẳng hàng” như sau:
V![]()
![]() í
dụ 1:
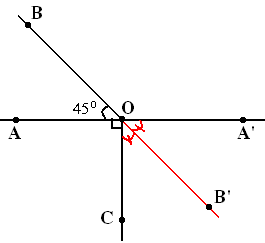
Trên đường thẳng AA’ lấy điểm O. Trên nửa mặt
phẳng bờ AA’ vẽ tia
í
dụ 1:
Trên đường thẳng AA’ lấy điểm O. Trên nửa mặt
phẳng bờ AA’ vẽ tia
O![]() B
sao cho AOB = 450.
Trên nửa mặt phẳng còn lại vẽ tia OC sao cho AOC = 900.
Gọi OB’ là tia phân giác của A’OC. Chứng minh ba điểm
B, O, B’ thẳng hàng
B
sao cho AOB = 450.
Trên nửa mặt phẳng còn lại vẽ tia OC sao cho AOC = 900.
Gọi OB’ là tia phân giác của A’OC. Chứng minh ba điểm
B, O, B’ thẳng hàng
G![]()
 iải
iải
A![]()
![]()
![]() ,
O, A’ thẳng hàng
AOA’ = 1800
,
O, A’ thẳng hàng
AOA’ = 1800
A![]() OC
+ COA’ = AOA’
OC
+ COA’ = AOA’
900
+ COA’ = 1800![]()
COA’ = 1800
– 900
= 900![]()
Vì OB’ là tia phân giác của COA’
![]()
![]()
![]()
![]()
![]()
![]() COB’ =
COB’ =
 =
=
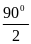 = 450
= 450
BOB’ = BOA + AOC + COB’
= 450 + 900 + 450 = 1800
Vậy ba điểm B, O, B’ thẳng hàng
V![]()
![]() í
dụ 2:
Cho góc vuông AOB và tia OC nằm trong góc đó. Vẽ tia OM sao
cho tia OA là tia phân giác của COM. Vẽ tia ON sao cho tia OB
là tia phân giác của CON. Chứng minh ba điểm M, O, N thẳng
hàng.
í
dụ 2:
Cho góc vuông AOB và tia OC nằm trong góc đó. Vẽ tia OM sao
cho tia OA là tia phân giác của COM. Vẽ tia ON sao cho tia OB
là tia phân giác của CON. Chứng minh ba điểm M, O, N thẳng
hàng.
G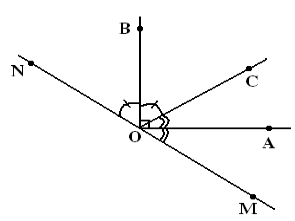
![]()
![]()
![]() iải
iải
![]()
![]() M,
O, N thẳng hàng
M,
O, N thẳng hàng ![]()
![]()
![]()
![]() OA là tia phân giác của COM
COM = 2 COA
OA là tia phân giác của COM
COM = 2 COA
![]()
![]()
![]() OB là tia phân giác của CON CON
= 2 COB
OB là tia phân giác của CON CON
= 2 COB
![]()
![]() MON =COM + CON
MON =COM + CON
![]()
![]() = 2COA + 2 COB
= 2COA + 2 COB
![]() = 2.(COA + COB)
= 2.(COA + COB)
= 2. AOB
= 2. 900
= 1800
Vậy ba điểm M, O, N thẳng hàng
Ví dụ 3: Cho ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA (tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm D sao cho CD = AB. Chứng minh ba điểm B, M, D thẳng hàng.
G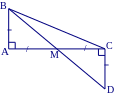 iải
iải
Xét
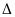 AMB
và
AMB
và
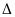 CMD
có:
CMD
có:
AB = DC (gt).

MA = MC (M là trung điểm AC)
Do đó:
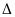 AMB
=
AMB
=
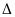 CMD
(c.g.c).
CMD
(c.g.c).
Suy ra:
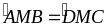
Mà
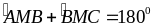 (kề bù)
(kề bù)
nên
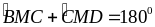 .
.
Vậy ba điểm B; M; D thẳng hàng.
Ví dụ 4: (Bài tập 55 trang 80 SGK Hình học 7 tập 2).
Cho hình vẽ. Chứng minh ba điểm B, D, C thẳng hàng
Giải
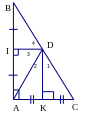
KD là đường trung trực của AC
 DA = DC
DA = DC
 ADC cân tại D
ADC cân tại D
Mà DK là đường trung trực
=> DK là đường phân giác
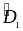 =
=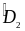 (1)
(1)
DI là đường trung trực của AB
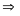 DA
= DB
DA
= DB
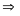 ABD
cân tại D
ABD
cân tại D
Mà DI là đường trung trực
=> DI là đường phân giác
=>
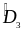 =
=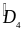 (2)
(2)
Từ (1) và (2) suy ra
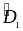 +
+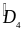 =
=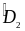 +
+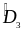
Ta có: DK // AI (cùng vuông góc với AC)
Mà
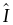
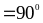 suy ra
suy ra
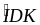
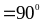 =>
=>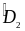 +
+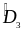 =
=
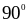
=>
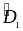 +
+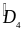 =
=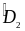 +
+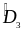 =
=
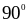
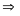
 =
=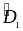 +
+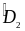 +
+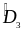 +
+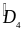
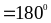
Vậy ba điểm B, D, C điểm thẳng hàng.
2. Vận dụng tiên đề Ơclít chứng minh hai đường thẳng cùng đi qua một điểm và cùng song song với một đường thẳng cho trước



=> A, B, C thẳng hàng
BC // a
AC // a
V![]()
![]()
![]()
![]() í
dụ 1:
Cho 2 góc AOM và MOB kề bù (theo hình vẽ)
í
dụ 1:
Cho 2 góc AOM và MOB kề bù (theo hình vẽ)
V![]() ẽ
tia MC sao cho 2 góc CMO, MOA so le trong và bằng nhau
ẽ
tia MC sao cho 2 góc CMO, MOA so le trong và bằng nhau
V![]() ẽ
tia MD sao cho 2 góc DMO, MOB so le trong và bằng nhau
ẽ
tia MD sao cho 2 góc DMO, MOB so le trong và bằng nhau
Chứng minh ba điểm C, M, D thẳng hàng
Giải![]()
![]()
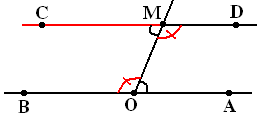 CMO
và MOA là cặp góc so le trong bằng nhau
CMO
và MOA là cặp góc so le trong bằng nhau
MC // OA
Mà B thuộc đường thẳng OA
![]()
![]()
MC //
AB
MC //
AB
DMO và MOB là cặp góc so le trong bằng nhau
MD // OB
Mà A thuộc đường thẳng OB
MD // AB
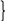 Ta
có MC //
AB
(cmt)
Ta
có MC //
AB
(cmt)
MD // AB (cmt)
Ba điểm C, M, D thẳng hàng (Tiên đề Ơclit)
Ví dụ 4: Cho ABC vuông tại A. Vẽ ACD vuông tại C có CD < AB. Vẽ đường thẳng m qua A và song song với BC. E là điểm nằm trên đường thẳng m sao cho E và C cùng thuộc nửa mặt phẳng bờ AB, AE = BC. Chứng minh ba điểm D, C, E thẳng hàng.
Giải
X ét
ét
 ABC
và
ABC
và
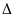 CEA
có:
CEA
có:
BC = EA (gt)
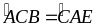 (hai góc so
le trong vì AE //
BC)
(hai góc so
le trong vì AE //
BC)
AC là cạnh chung
Vậy:
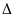 ABC
=
ABC
=
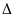 CEA
(c.g.c)
CEA
(c.g.c)
=>
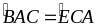
Mà
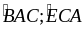 là 2 góc so le trong
là 2 góc so le trong
=> CE // AB
Mặt khác
CD
AC (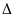 ACD
vuông tại C)
ACD
vuông tại C)
và AB
AC (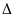 ABC
vuông tại A)
ABC
vuông tại A)
=> CD // AB
Ta có CE // AB, CD // AB
Theo tiên đề Ơ-Clit ta có hai đường thẳng CE, CD trùng nhau
Vậy ba điểm D, C, E thẳng hàng
Ví dụ 2: Cho hai đoạn thẳng AC và BD cắt nhau tai trung điểm O của mỗi đoạn. Trên tia AB lấy lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung điểm AN. Chúng minh ba điểm M, C, N thẳng hàng.
Giải
Xét
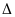 AOD
và
AOD
và
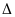 COB
có:
COB
có:
OA = OC (vì O là trung điểm AC)
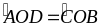 (hai góc đối đỉnh)
(hai góc đối đỉnh)
O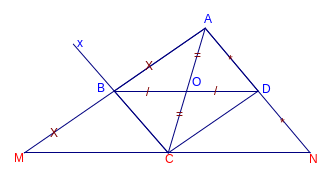 D
= OB (vì O là trung điểm BD)
D
= OB (vì O là trung điểm BD)
Vậy
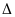 AOD
=
AOD
=
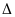 COB
(c.g.c)
COB
(c.g.c)
Suy ra:
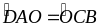 .
.
Do đó: AD // BC.
Nên
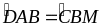 (ở
vị trí đồng vị)
(ở
vị trí đồng vị)
Xét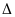 DAB
và
DAB
và
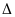 CBM
có :
CBM
có :
AD = BC ( do
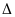 AOD
=
AOD
=
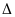 COB),
COB),
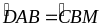 (hai
góc đồng vị)
(hai
góc đồng vị)
AB = BM ( B là trung điểm AM)
Vậy
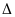 DAB
=
DAB
=
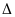 CBM
(c.g.c).
CBM
(c.g.c).
Suy ra
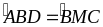 .
Do đó BD //
CM. (1)
.
Do đó BD //
CM. (1)
Lập luận tương tự ta được BD // CN. (2)
Từ (1) và (2) , theo tiên đề Ơ-Clit suy ra ba điểm M, C, N thẳng hàng.
Ví dụ 3: Cho ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung điểm BD và N là trung điểm EC. Chứng minh ba điểm E, A, D thẳng hàng.
 Giải
Giải
Xét
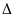 BMC
và
BMC
và
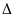 DMA
có:
DMA
có:
MC = MA (do M là trung điểm AC)
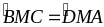 (hai góc đối đỉnh)
(hai góc đối đỉnh)
MB = MD (do M là trung điểm BD)
Vậy:
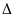 BMC
=
BMC
=
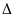 DMA
(c.g.c)
DMA
(c.g.c)
Suy ra:
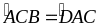
Mà
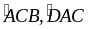 là
hai góc này ở
vị trí so le trong
là
hai góc này ở
vị trí so le trong
nên BC // AD (1)
Chứng minh tương tự : BC // AE (2)
Điểm A ở ngoài BC có một và chỉ một đường thẳng song song BC
nên từ (1) và (2) và theo Tiên đề Ơ-Clit
Suy ra ba điểm E, A, D thẳng hàng.
3. Chứng minh hai đường thẳng cùng đi qua một điểm và cùng vuông góc với
một đường thẳng cho trước:
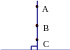
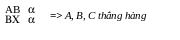
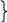

a
Ví
dụ
1:
Cho
ABC,
trên
tia
đối
của
tia
AB
lấy
điểm
D
sao
cho
AD
=
AB.
Trên
tia
đối
của
tia
AC
lấy
điểm
E
sao
cho
AE
=
AC.
Vẽ
AH
vuông
góc
BC
(H
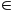 BC).
BC).
Trên đoạn DE lấy điểm K sao cho BH = DK. Chứng minh ba điểm A, H, K thẳng hàng.
Giải
Có ADE
= ABC
(vì AE = AC, AD = AB,
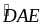 =
=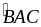 )
)
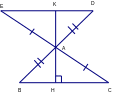
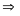
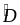 =
=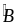 mà
mà
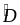 ,
,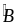 là 2 góc so le trong
là 2 góc so le trong
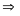 DE //
BC
DE //
BC
AHB = AKD
(vì AB=
AD, BH
= DK,
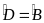 )
)
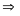
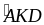 =
=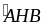
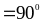
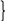
=> AK DE
Mà DE // BC
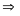 AK
BC
AK
BC
mà AH BC
Suy ra ba điểm K, A, H thẳng hàng.
V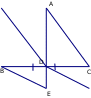 í
dụ 2: Cho
ABC
cân tại A, AD là đường trung tuyến. Trên nửa mặt phẳng
bờ BC không chứa điểm A vẽ DCE
vuông tại D. Chứng minh ba điểm A, D, E thẳng hàng.
í
dụ 2: Cho
ABC
cân tại A, AD là đường trung tuyến. Trên nửa mặt phẳng
bờ BC không chứa điểm A vẽ DCE
vuông tại D. Chứng minh ba điểm A, D, E thẳng hàng.
Giải
Ta có ABC cân tại A (gt)
AD là đường trung tuyến (gt)
=> AD là đường cao của ABC
=> AD BC
Mà DE BC (DCE vuông tại D)
Do vậy hai đường thẳng AD, DE trùng nhau
Vậy ba điểm A, D, E thẳng hàng
V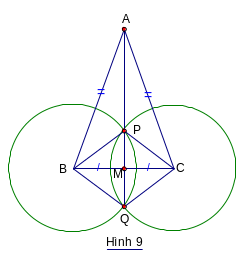 í
dụ 3:
Cho ABC
có AB = AC.
Gọi M là trung điểm BC.
Vẽ hai đường
tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt
nhau tại hai điểm P và Q. Chứng minh ba điểm A, P, Q thẳng
hàng.
í
dụ 3:
Cho ABC
có AB = AC.
Gọi M là trung điểm BC.
Vẽ hai đường
tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt
nhau tại hai điểm P và Q. Chứng minh ba điểm A, P, Q thẳng
hàng.
Giải
Xét ΔABM và ΔACM có:
AB =AC (gt)
AM chung
MB = MC (M là trung điểm BC)
Vậy ΔABM = ΔACM (c.c.c)
Suy ra:
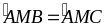 (hai
góc tương ứng)
(hai
góc tương ứng)
Mà
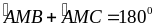 (hai
góc kề bù)
(hai
góc kề bù)
nên
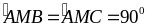
Do đó: AM
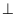 BC (đpcm)
BC (đpcm)
Chứng minh tương tự ta được: ΔBPM = ΔCPM (c.c.c).
Suy ra:
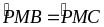 (hai
góc tương ứng)
(hai
góc tương ứng)
mà
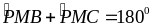
nên
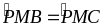 =
900
=>
PM
BC.
=
900
=>
PM
BC.
Lập luận tương tự QM BC
Từ điểm M trên BC có AM BC, PM BC, QM BC
Nên ba điểm A, P, Q thẳng hàng (đpcm)
V í
dụ 4: Cho
ABC
có AB = 5, AC = 12, BC = 13. Vẽ ACD
sao cho AD = 16, CD = 20. Chứng minh ba điểm B, A, D thẳng
hàng
í
dụ 4: Cho
ABC
có AB = 5, AC = 12, BC = 13. Vẽ ACD
sao cho AD = 16, CD = 20. Chứng minh ba điểm B, A, D thẳng
hàng
Giải
Ta có AB2 + AC2 = 52 + 122 = 169
BC2 = 132 = 169
Nên AB2 + AC2 = BC2
=> ABC vuông tại A (định lí Py-ta-go đảo)
=> AB AC
Tương tự: ACD có AC2 + AD2 = CD 2 = 400
=> ACD vuông tại A (định lí Py-ta-go đảo)
=> AD AC
Ta có AB AC và AD AC
=> Hai đường thẳng AB, AD trùng nhau
Vậy ba điểm B, A, D thẳng hàng
4. Chứng minh ba điểm cùng thuộc tia phân giác của một góc:
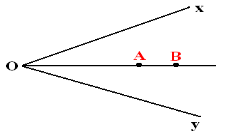
 Tia
OA là tia phân giác của
Tia
OA là tia phân giác của
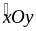
Tia
OB là tia phân giác của
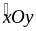
A, O, B thẳng hàng
Ví dụ 1: Cho ABC có AB = AC. Gọi M là một điểm nằm trong tam giác sao cho MB = MC. Gọi N là trung điểm của BC. Chứng minh ba điểm A, M, N thẳng hàng.

A
Giải

ABM ACM
(vì AM chung, AB = AC, MB = MC )

M
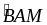 =
=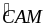
AM
là
tia
phân
giác
 (1)
(1)
Tương tự ABN ACN (c.c.c)



C
N
B
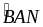 =
=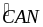
AN
là
tia
phân
giác
 (2)
(2)
Từ (1), (2) suy ra ba A, M, N điểm thẳng hàng.
Ví dụ 2:
Cho
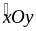 .
Trên hai cạnh
Ox và Oy lấy lần lượt hai điểm B và C sao cho OB = OC. Vẽ
đường tròn tâm B và tâm C có cùng bán kính sao cho chúng
cắt nhau tại hai điểm A và D nằm trong góc xOy. Chứng
minh ba điểm O, A, D thẳng hàng.
.
Trên hai cạnh
Ox và Oy lấy lần lượt hai điểm B và C sao cho OB = OC. Vẽ
đường tròn tâm B và tâm C có cùng bán kính sao cho chúng
cắt nhau tại hai điểm A và D nằm trong góc xOy. Chứng
minh ba điểm O, A, D thẳng hàng.
Giải
Xét ΔBOD và ΔCOD có:
O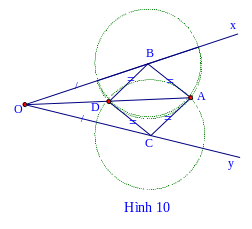 B
= OC (gt)
B
= OC (gt)
OD chung
BD = CD (D là giao điểm của
hai đường tròn tâm B và tâm C cùng bán kính).
Vậy ΔBOD =ΔCOD (c.c.c).
Suy ra :
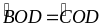 .
.
Điểm D nằm trong
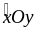
nên tia OD nằm giữa hai tia Ox và Oy.
Do đó OD là tia phân giác
của
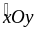 .
.
Chứng minh tương tự ta
được OA là tia phân giác của
 .
.
 chỉ
có một tia phân giác nên hai tia OD và OA trùng nhau.
chỉ
có một tia phân giác nên hai tia OD và OA trùng nhau.
Vậy ba điểm O, D, A thẳng hàng.
5. Chứng minh ba điểm cùng thuộc đường trung trực của một đoạn thẳng


=> A, B, C thẳng hàng
A thuộc đường trung trực của MN
B thuộc đường trung trực của MN
C thuộc đường trung trực của MN
Ví dụ 1: Cho ABC, DBC và EBC cân có chung đáy BC.
C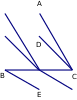 hứng
minh
rằng
ba
điểm
A,
D,
E
thẳng
hàng.
hứng
minh
rằng
ba
điểm
A,
D,
E
thẳng
hàng.
Giải
Ta có ABC cân tại A suy ra AB = AC
A thuộc đường trung trực của BC (1)
DBC cân tại D suy ra DB = DC
D thuộc đường trung trực của BC (2)
EBC cân tại E suy ra EB = EC
E thuộc đường trung trực của BC (3)
Từ (1), (2), (3) suy ra ba điểm A, D, E thẳng hàng.
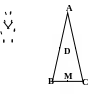 Ví
dụ
2:
Cho
ABC cân tại A, M là trung điểm BC. Đường trung trực của
AB, AC cắt nhau ở D. Chứng minh ba điểm A, M, D thẳng hàng
Ví
dụ
2:
Cho
ABC cân tại A, M là trung điểm BC. Đường trung trực của
AB, AC cắt nhau ở D. Chứng minh ba điểm A, M, D thẳng hàng
Giải
Ta có : AB = AC (gt)
MB = MC (M là trung điểm BC)
Suy ra: AM là đường trung trực của đoạn BC (1)
ABC có đường trung trực của AB và AC cắt nhau tại D
Suy ra: D là giao điểm 3 đường trung trực trong ABC
Nên: D thuộc đường trung trực của BC (2)
Từ (1) và (2) suy ra ba điểm A, M, D thẳng hàng
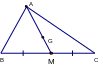
6. Áp dụng đường trung tuyến của một tam giác thì phải đi qua trọng tâm.
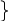
G là trọng tâm tam giác ABC

=> A, G, M thẳng hàng
AM là trung tuyến tam giác ABC
Ví dụ 1: Cho ABC vuông tại A, có BC = 10cm, AC = 8cm. Lấy điểm M trên AB sao cho BM = 4cm. Vẽ điểm D sao cho A là trung điểm DC, gọi N là trung điểm BD. Chứng minh ba điểm C, M, N thẳng hàng
 Giải
Giải
Áp dụng định lý Pythagore
Tính được AB = 6cm
DBC có BA là trung tuyến
và
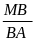 =
=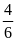 =
=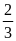
BM =
BM =
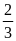 BA
BA
Vậy M là trọng tâm của DBC
N là trung điểm BD suy ra CN là trung tuyến BDC
Trung tuyến CN phải đi qua trọng tâm M
Vậy ba điểm C, M, N thẳng hàng
Ví dụ 2: Cho ABC, kẻ trung tuyến AM. Trên AM lấy hai điểm P, Q sao cho AQ = PQ = PM. Gọi E là trung điểm của AC. Chứng minh ba điểm B, P, E thẳng hàng.
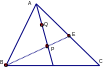
Giải
ABC có AM là trung tuyến
mà AQ = QP = PM (gt)

M
AP
=
 AM
AM
P là trọng tâm ABC
Vì
E
là
trung
điểm
của
AC
nên
BE
là
trung
tuyến
của
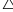 ABC
ABC
BE đi qua trọng tâm P hay ba điểm B, P, E thẳng hàng.

A
7. Chứng minh đường phân giác của tam giác thì đi qua giao điểm chung của chúng:

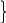
I
I là
giao
điểm
2
đường
phân
giác
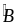 ,
,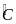
AD
là
phân
giác
của
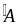



C
D
B
D thẳng hàng.
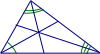
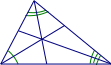
Ví dụ 1: Cho ABC cân tại A. Vẽ phân giác BD và CE cắt nhau tại I. Gọi M là trung điểm BC. Chứng minh ba điểm A, I, M thẳng hàng
![]()
![]()
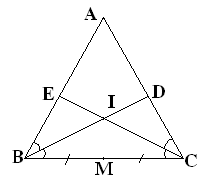 Giải
Giải
Ta có ABC có phân giác của B và C cắt nhau tại I
suy ra I là giao điểm của 3 đường phân giác trong tam giác
ABC cân tại A có
AM là đường trung tuyến ứng với cạnh đáy
nên AM cũng là phân giác.
Đường phân giác AM phải đi qua giao điểm I
Vậy ba điểm A, I, M thẳng hàng
Ví dụ 2: Cho ABC, các tia phân giác các góc A và C cắt nhau tại I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh ba điểm B, I, K thẳng hàng.
Giải
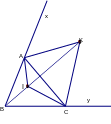
Vì K thuộc đường phân giác góc ngoài tại A
nên K cách đều hai cạnh Ax và AC (1)
Vì K thuộc đường phân giác góc ngoài tại C
nên K cách đều hai cạnh Cy và AC (2)
Từ (1) và (2)
suy ra K cách đều 2 cạnh Ax và Cy
Hay K cách đều hai cạnh BA và BC
KB
là
tia
phân
giác
vì I là giao điểm của
hai tia phân giác
 ,
,

nên:
BI là tia phân
giác
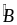 (gt)
(gt)
=> Ba điểm B, I, K thẳng hàng
8. Chứng minh đường cao của tam giác thì đi qua trực tâm của tam giác đó:

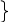
H là trực tâm ABC
AD là đường cao ABC
=> A, H, D ba điểm thẳng hàng
Ví dụ 1: Cho ABC cân tại A, vẽ đường cao BH và CK cắt nhau tại I. Gọi M là trung điểm của BC. Chứng minh ba điểm A, I, M thẳng hàng.
Giải
Vì I là giao điểm hai đường cao BH và CK
nên I là trực tâm ABC
ABC cân tại A có
AM là đường trung tuyến
Nên AM cũng là đường cao.
=> Đường cao AM đi qua trực tâm I
=> Ba điểm A, I, M thẳng hàng.
Ví dụ
2: Cho
ABC
vuông
tại
A.
Tia phân giác
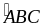 cắt cạnh AC tại D. Trên cạnh BC lấy E sao cho BE = AB.
Đường thẳng qua C vuông góc với BD cắt AB ở F. Chứng
minh
ba
điểm D,
E,
F
thẳng
hàng.
cắt cạnh AC tại D. Trên cạnh BC lấy E sao cho BE = AB.
Đường thẳng qua C vuông góc với BD cắt AB ở F. Chứng
minh
ba
điểm D,
E,
F
thẳng
hàng.
Giải
X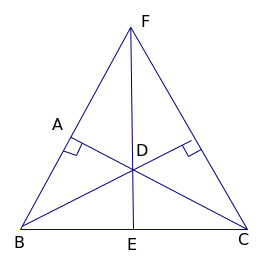 ét
ABD
và EBD
có
ét
ABD
và EBD
có
AB = BE (gt)
 =
=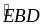 (BD
là phân giác
(BD
là phân giác
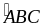 )
)
BD là cạnh chung
Do đó ABD = EBD (c-g-c)
=>
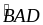 =
=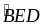
Mà
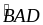
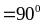 (gt)
(gt)
Nên
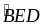
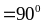
=> DE BC
Mặt khác FBC có
CA, BD là 2 đường cao cắt nhau tại D (BD AC (gt), CA AB (gt))
Nên D là trực tâm của FBC
=> FD BC
Ta có DE BC, FD BC
=> Hai đường thẳng DE, DF trùng nhau
Vậy ba điểm D, E, F thẳng hàng.

9. Chứng minh đường trung trực của một cạnh thì đi qua giao điểm hai đường trung trực của hai cạnh còn lại:
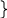
O là giao điểm 2 đường trung trực của 2 cạnh AC và BC
EF là đường trung trực của cạnh AB
=> E, F,O thẳng hàng
Ví dụ 1: Cho ABC cân tại A, M là trung điểm của BC. Đường trung trực của AB, AC cắt nhau ở D. Chứng minh ba điểm A, D, M thẳng hàng.
Giải
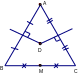
ABC cân tại A có MB = MC
nên: AM là đường trung tuyến ABC
=> AM cũng là đường trung trực của ABC
Mà D là giao điểm hai đường trung trực cạnh AB, AC
Nên AM đi qua D
=> Ba điểm A, D, M thẳng hàng.
Ví dụ 2: Cho ABC vuông tại A (AB < AC). Trên nửa mặt phẳng bờ BC không chứa điểm A, lấy các điểm D, E sao cho BD = BA và BD BA, BE = BC và BE BC. Gọi M là trung điểm của đoạn thẳng CE. Chứng minh ba điểm A, D, M thẳng hàng.
Giải
Xét ABC và DBE có:
AB = BD (gt)
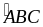 =
=
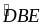 (cùng
phụ với
(cùng
phụ với
 )
)
BC = BE (gt)
Do đó ABC = DBE (c-g-c)
=>
 =
=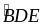
Nên
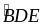
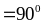
Gọi F là giao điểm của ED và AC
Ta có AB BD, DF BD
=> AB // DF
Xét ABD và DFA có:
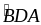 =
=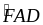
AD là cạnh chung
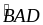 =
=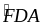
Do đó ABD = DFA (g-c-g)
=> BD = FA và AB = DF
Mà AB = BD (gt)
Do đó AB = BD = AF = DF
Chứng
minh được BM = FM =
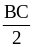
Ta có AB = AF, BD = DF, BM = FM
=> A, D, M cùng nằm trên đường trung trực của đoạn thẳng BF
Vậy ba điểm A, D, M thẳng hàng.
10. Sử dụng phương pháp hình duy nhất
Để chứng minh 3 điểm A, B, C thẳng hàng, trong đó C thuộc hình H (hình H là đường thẳng, tia, đoạn thẳng ...) chúng ta có thể gọi C’ là giao điểm của AB với hình H tìm cách chứng minh 2 điểm C và C’ trùng nhau
Ví dụ 1: Cho ABC. Vẽ ABD sao cho D nằm trên trên nửa mặt phẳng bờ AB không chứa C và AD // BC. Gọi M là trung điểm cạnh AC. Trên tia đối của tia MB lấy điểm E sao cho ME = MB. Chứng minh rằng ba điểm D, A, E thẳng hàng.
Giải
G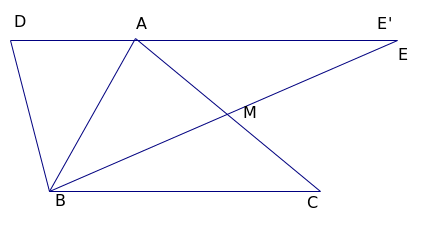 ọi
E’ là giao điểm của BM và AD
ọi
E’ là giao điểm của BM và AD
Xét MAE’ và MCB có
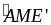 =
=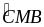 (đối
đỉnh)
(đối
đỉnh)
MA = MC (M là trung điểm AC)
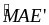 =
=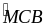 (so
le trong vì AE’ // BC)
(so
le trong vì AE’ // BC)
Do đó MAE’ = MCB (g-c-g)
=> ME’ = MB
Mà ME = MB (gt)
Do đó ME = ME’ => E E’.
Vậy ba điểm D, A, E thẳng hàng
Ví dụ 2: Cho ΔABC cân tại A. Trên các cạnh AB, AC lần lượt lấy D, E sao cho AD = AE. Gọi M, N lần lượt là trung điểm các đoạn thẳng BC, DE. Chứng minh rằng ba điểm A, M, N thẳng hàng.
G iải
iải
Gọi N’ là giao điểm AM và DE
ΔABC cân tại A
AM là đường trung tuyến (M là trung điểm của cạnh BC)
=> AM
là đường phân giác của
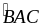
ΔADE cân tại A
AN’ là đường phân giác
=> AN’ là đường trung tuyến của ΔADE
=> N’ là trung điểm của cạnh DE
Mà N là trung điểm của cạnh DE
Do đó N’ N
Vậy ba điểm A, M, N thẳng hàng.
Ví dụ 3: Cho ABC cân tại A. Trên cạnh AB lấy điểm M, trên tia đối tia CA lấy điểm N sao cho BM = CN. Gọi K là trung điểm MN. Chứng minh ba điểm B, K, C thẳng hàng
Giải
K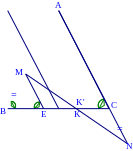 ẻ
ME // AC (E
ẻ
ME // AC (E
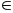 BC)
BC)
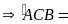
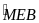 (hai góc đồng vị)
(hai góc đồng vị)
Mà
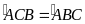 nên
nên
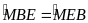
Vậy ΔMBE cân ở M.
Do đó: MB = ME
Mà MB = NC
ta được ME = CN.
Gọi K’ là giao điểm của BC và MN.
Xét ΔMEK’ và ΔNCK’ có:
 (so le trong của ME //AC)
(so le trong của ME //AC)
ME = CN (chứng minh trên)
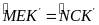 (so le trong của ME //AC)
(so le trong của ME //AC)
Do đó : ΔMEK’ = ΔNCK’ (g.c.g)
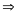 MK’
= NK’.
MK’
= NK’.
Vậy K’ là trung điểm MN,
mà K là trung điểm MN
nên K
 K’
K’
Do đó ba điểm B, K, C thẳng hàng.
Ngoài Phương Pháp Chứng Minh Ba Điểm Thẳng Hàng Có Lời Giải thì các tài liệu học tập trong chương trình 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm






