Giáo Án Hình Học 7 Phương Pháp Mới 5 Hoạt Động Học Kì 2
Có thể bạn quan tâm
Giáo Án Hình Học 7 Phương Pháp Mới 5 Hoạt Động Học Kì 2 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Giáo Án Hình Học 7 Phương Pháp Mới 5 Hoạt Động Học Kỳ 2 tập trung vào việc giúp học sinh hiểu và áp dụng những kiến thức hình học cơ bản một cách sâu sắc và linh hoạt. Bằng cách tạo ra môi trường học tập tích cực, tài liệu này giúp học sinh phát triển khả năng tư duy logic, trực quan và giải quyết vấn đề.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
Tuần: 20 Tiết KHGD: 34 |
Ngày soạn: 06/01/2018 Ngày dạy: 08/01/2018 |
|
LUYỆN TẬP VỀ BA TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC |
|
|
I. MỤC TIÊU:
1. Kiến thức: Củng cố ba trường hợp bằng nhau của hai tam giác.
2. Kĩ năng: Rèn kỹ năng vẽ hình chứng minh, chứng tỏ được rằng 2 tam giác bằng nhau từ đó suy ra được hai cạnh, hai góc tương ứng bằng nhau.
3. Thái độ: Phát huy trí lực của học sinh.
4. Xác định nội dung trọng tâm của bài: Củng cố trường hợp bằng nhau góc cạnh góc, và áp dụng trường hợp nào vào tam giác vuông, củng cố hai trường hợp (c.c.c), (c.g.c).
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, compa, thước đo góc, êke, bảng phụ.
2. Học sinh: Thước thẳng, compa, thước đo góc, Sgk.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Các trường hợp bằng nhau của tam giác. |
Biết các trường hợp bằng nhau của tam giác. |
|
Vận dụng chứng minh hai tam giác bằng nhau để giải các bài toán liên quan. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (10')
HS1: Phát biểu trường hợp bằng nhau g.c.g của tam giác. (5đ)
Phát biểu hệ quả 1, 2 về trường hợp bằng nhau của 2 vuông. (5đ)
HS2: Bài tập 39.Sgk/124 tập 1. Đáp án : H.105: AHB = AHC (c.g.c); 3đ
H.107: ABD = ACD(ch-gn); 2đ
H.106: DKE = DKF (g.c.g) 2đ
H.108: ABD = ACD(ch-gn)
BDE = CDH (g.c.g); ABH = ACE (g.c.g) 3đ H. 107 H. 108
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Các em đã biết các trường hợp bằng nhau của hai tam giác. Hôm nay, chúng ta sẽ luyện kĩ năng nhận biết hai tam giác bằng nhau theo ba trường hợp đã học và vận dụng để xác định hai cạnh, hai góc tương ứng bằng nhau. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Vận dụng (27’)
(1) Mục tiêu: HS vận dụng kiến thức đã học để giải một số dạng toán cơ bản. HS có kĩ năng vẽ hình, kĩ năng chứng minh và kĩ năng suy luận và phát triển bài toán hình học.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng phấn, sgk, thước đo độ, thước thẳng có chia khoảng.
(5) Sản phẩm: Lời giải bài 40, 41, 43.Sgk
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1
GiảiXét 2 vuông BEM và CFM Có BM = CM (gt)
Nên BEM = CFM (ch-gn) BE = CF (2 cạnh t/ứng) 2
Chứng minhXét EIC và FIC có: Ê
=
cạnh
IC chung;
Nên EIC = FIC (ch-gn) IE = IF (1) Xét BDI và BEI Có
BI
cạnh chung;
Nên BDI = BEI (ch-gn) ID = IE (2) Từ (1) và (2) ID = IE = IF 3
Chứng minh a) Xét OAD và OCB, có OA = OC (gt) Ô: góc chung OD = OB (gt) Nên OAD = OCB (c.g.c) AD = BC b) Vì OAD = OCB
Â2
=
Lại có: AB = OB OA CD = OD OC Mà OA = OC, OB = OD (gt) AB = CD Xét EAB và ECD Â2
=
Do đó EAB = ECD (g.c.g) EA = EC |
H: Qua hình vẽ hãy dự đoán xem BE = CF? Nếu có hãy c/minh điều đó? H: 2 cạnh BE và CF nằm trong 2 nào? 2 đó có thể bằng nhau không? Tại sao? GV gọi 1HS lên bảng trình bày Gọi HS nhận xét. GV sửa sai (nếu có)
GV gợi ý: Để chứng minh ID = IE = IF Ta tách ra từng cặp và dựa vào gt để chứng minh: ID = IE ; IE = IF Xét 2 cặp vuông có liên quan đến 2 tia phân giác RI và CI GV gọi HS lên bảng trình bày GV gọi HS nhận xét GV sửa sai hoàn chỉnh (nếu có) Qua hai bài tập 40 và 41 ta đã vận dụng điều gì? để kết luận rút ra hai đoạn thẳng bằng nhau?
GV treo bảng phụ bài 43 GV Gọi HS lên bảng vẽ hình và ghi GT, KL
GV gợi ý: Xét AD, BC nằm trong hai tam giác nào? và 2 tam giá đó có bằng nhau không?
GV gọi HS lên bảng trình bày chứng minh
|
HS: Đọc kỹ đề. Vẽ hình ghi GT, KL ABC (AB BC) GT M là trung điểm BC BE AM; CF AM
KL So sánh BE, CF
HS: lên bảng trình bày
HS: Nhận xét
HS: đọc đề vẽ hình và ghi GT, KL ABC, RI, CI là GT
phân giác
ID AB; IE BC IF AC KL ID = IE = IF
HS : Lên bảng trình bày
HS : Nhận xét
HS Trả lời: Áp dụng hệ quả 2 để chứng minh 2 tam giác vuông bằng nhau từ đó rút ra các cạnh tương ứng bằng nhau. HS: đọc kỹ đề bài 43 1HS lên bảng giải, vẽ hình ghi GT, KL GT OA < OB; C, D Oy OC = OA, OD = OB AD BC = E
KL AD = BC EAB = ECD
HS: nghe GV gợi ý
HS1: Câu a
HS2: Câu b
|
Năng lực tư duy, giải quyết vấn đề, vận dụng
Năng lực giải quyết vấn đề, vận dụng
|
C. LUYỆN TẬP: Đã thực hiện ở trên
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG:
HOẠT ĐỘNG 3. Tìm tòi, mở rộng (5’)
(1) Mục tiêu: Tạo cho Hs nhu cầu tìm hiểu ứng dụng của tam giác trong đời sống và trong khoa học. Hình thành năng lực ứng dụng CNTT, tự nghiên cứu, quan sát, tổng hợp, …
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, KT động não.
(3) Hình thức tổ chức hoạt động: Hoạt động cá nhân.
(4) Phương tiện dạy học: Sgk, trên mạng Internet
(5) Sản phẩm: Kết quả tìm hiểu của các nhóm về ứng dụng của hình ảnh tam giác trong thời trang, kiến trúc, các lĩnh vực khác trong đời sống.
GV: Chuyển giao nhiệm vụ học tập. 1) Em hãy thảo luận với các bạn và tìm hiểu trên Internet: Hình ảnh tam giác còn được vận dụng trang trí trong thời trang, trong kiến trúc và trong đời sống. Gv phát phiếu tập cho học sinh có nôi dung như trên. + Yêu cầu học sinh về nhà làm việc theo nhóm để thảo luận, cùng nhau tìm hiểu trên mạng Internet về ứng dụng của hình ảnh tam giác trong thời trang, kiến trúc, các lĩnh vực khác trong đời sống. Sau khi tìm hiểu các em có thể in ra hoặc chụp ảnh hoặc quay video. |
Học sinh đọc kỹ đề bài
Học sinh suy nghĩ trả lời.
Hs có thể về nhà làm việc theo nhóm để hoàn thành nội dung phiếu học tập.
|
E. HƯỚNG DẪN VỀ NHÀ (2’)
Ôn lại các trường hợp bằng nhau của tam giác và các hệ quả của chúng.
Bài tập về nhà 43; 44; 45.Sgk/125.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Các khẳng định sau đây đúng hay sai? (MĐ1)
a)
Nếu ABC
và A’B’C’
có: Â = Â’;
![]() ;
AC = A’C’ thì
ABC = A’B’C’(theo
trường hợp g.c.g)
.
;
AC = A’C’ thì
ABC = A’B’C’(theo
trường hợp g.c.g)
.
b) Nếu MIN và RST có MI = RT; MN = RS; IN = TS thì MIN = RST (theo trường hợp c.c.c.) .
Tuần: 20 Tiết KHGD: 35 |
Ngày soạn: 06/01/2018 Ngày dạy: 11/01/2018 |
|
LUYỆN TẬP VỀ BA TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC (tt) |
|
|
I. MỤC TIÊU:
1. Kiến thức: Tiếp tục củng cố cách chứng minh hai tam giác bằng nhau theo ba trường hợp bằng nhau của hai tam giác thường và các trường hợp áp dụng vào tam giác vuông.
2. Kĩ năng: Rèn kỹ năng chứng minh hai tam giác bằng nhau.
3. Thái độ: Giáo dục tính chính xác, óc tư duy, sáng tạo.
4. Xác định nội dung trọng tâm của bài: Củng cố trường hợp bằng nhau góc cạnh góc, và áp dụng trường hợp nào vào tam giác vuông, củng cố hai trường hợp (c.c.c), (c.g.c).
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực sử dụng các công thức tổng quát, tự học, tính toán, sử dụng ngôn ngữ toán học.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, compa, thước đo góc, êke, bảng phụ.
2. Học sinh: Thước thẳng, compa, thước đo góc, Sgk.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Các trường hợp bằng nhau của tam giác. |
Biết các trường hợp bằng nhau của tam giác. |
Chứng minh được 2 đoạn thẳng bằng nhau, 2 góc bằng nhau dựa vào việc c/m 2 tam giác bằng nhau. |
Vận dụng chứng minh hai tam giác bằng nhau để giải các bài toán liên quan. |
|
III. HOẠT ĐỘNG DẠY – HỌC
* Kiểm tra bài cũ: (5’)
Phát biểu ba trường hợp bằng nhau của hai tam giác? (5đ)
Trong hình vẽ sau, hãy chỉ ra các cặp bằng nhau và giải thích. (5đ)

Đáp án: AOB = COD (c.g.c) ; AOD = COB (c.g.c) ;
ABC = CDA (c.c.c) ; ADB = CBD (c.c.c).
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Tiết trước đã luyện tập các trường hợp bằng nhau của hai tam giác. Hôm nay, chúng ta tiếp tục rèn kỹ năng chứng minh hai tam giác bằng nhau. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Bài tập tính góc (29’)
(1) Mục tiêu: HS vận dụng kiến thức đã học để giải một số dạng toán cơ bản. HS có kĩ năng vẽ hình, kĩ năng chứng minh và kĩ năng suy luận và phát triển bài toán hình học.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng phấn, sgk, thước đo độ, thước thẳng có chia khoảng.
(5) Sản phẩm: Lời giải bài 44, 45.Sgk
Nội dung |
Hoạt động của GV và HS |
|
NL hình thành |
1
Chứng minh: a)
Trong
Mà
Suy
ra
Xét
AD cạnh chung
Nên
b) Từ a) suy ra AB = AC (2 cạnh tương ứng). 2
a) Từ hình vẽ ta có: AEB = CGD (c.g.c) AB = CD CFB = AHD (c.g.c) BC = AD b) ABD = CDB (c.c.c)
AB//CD (có hai góc bằng nhau ở vị trí Slt). |
GV: Yêu cầu học sinh đọc đề bài, vẽ hình và ghi gt, kl.
H
H: Hai tam giác đó bằng nhau theo trường hợp nào?
GV: Từ a) suy ra được điều gì ?
GV: Vẽ hình và nêu hướng chứng minh.
GV: Vậy em nào có thể giải thích được ?
H: Làm như thế nào có thể chỉ ra được AB//CD ?
GV: Gọi HS lên bảng làm. |
HS: Đọc kỹ đề. Vẽ hình ghi GT, KL Gt
ABCcó
Kl a) ADB = ADC b) AB = AC
HS: Hoạt động nhóm và trả lời.
HS: Lên bảng trình bày.
HS: Trả lời.
|
Năng lực tự học và tính toán, sử dụng ngôn ngữ toán học.
Năng lực sử dụng các công thức tổng quát |
C. LUYỆN TẬP: Đã thực hiện ở trên
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG:
HOẠT ĐỘNG 3. Tìm tòi, mở rộng (8’)
(1) Mục tiêu: Rèn kĩ năng vẽ hình cho học sinh. HS biết chứng minh một đường thẳng là đường trung trực của đoạn thẳng, chứng minh 2 tam giác bằng nhau.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, KT động não.
(3) Hình thức tổ chức hoạt động: Hoạt động cá nhân.
(4) Phương tiện dạy học: Bảng, phấn, Sgk, dụng cụ học tập
(5) Sản phẩm: Hình vẽ và phần chứng minh của Hs.
Bài tập: Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a. GV: Chuyển giao nhiệm vụ học tập. Yêu cầu hs vẽ hình theo hướng dẫn. Gv hướng dẫn và rèn cho học sinh kĩ năng vẽ hình và kĩ năng sử dụng dụng cụ vẽ hình. Gv hướng dẫn hoc sinh chứng minh AD vuông góc với BC. Gv đặt câu hỏi để HS tự phát hiện ra AD là đường trung trực của BC. - Nếu hết giờ Gv yêu cầu hs về nhà chứng minh AD là đường trung trực của BC - Nhận xét, đánh giá, tổng hợp kĩ năng vẽ hình, kĩ năng sử dụng dụng cụ vẽ hình.
|
Học sinh đọc kỹ đề bài
Hs vẽ hình theo hướng dẫn.
|
E. HƯỚNG DẪN VỀ NHÀ (2’)
Ôn lại các trường hợp bằng nhau của tam giác và các hệ quả của chúng.
Về nhà làm các bài tập trong SBT. Xem trước bài “Tam giác cân”
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Phát biểu 3 trường hợp bằng nhau của 2 tam giác? (MĐ1)
Câu 2: Làm bài tập (MĐ2,3)
Tuần: 20 Tiết KHGD: 36 |
Ngày soạn: 06/01/2018 Ngày dạy: 12/01/2018 |
|
§6. TAM GIÁC CÂN |
|
|
I. MỤC TIÊU:
1. Kiến thức: HS nắm được định nghĩa tam giác cân, tam giác vuông cân, tam giác đều. Tính chất về góc của tam giác cân, tam giác vuông cân, tam giác đều.
2. Kĩ năng: Biết vẽ tam giác cân, tam giác vuông cân. Biết chứng minh 1 tam giác là tam giác cân, tam giác vuông cân, tam giác đều. Biết vận dụng các tính chất của tam giác cân, tam giác vuông cân, tam giác đều để tính số đo góc, để chứng minh các góc bằng nhau.
3. Thái độ: Phát huy tư duy nhanh nhạy, hoạt bát của học sinh
4. Xác định nội dung trọng tâm của bài: Nắm được định nghĩa tam giác cân, tam giác vuông cân, tam giác đều. T/chất về góc của tam giác cân, tam giác vuông cân, tam giác đều.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, compa, thước đo góc, êke, bảng phụ.
2. Học sinh: Thước thẳng, compa, thước đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Tam giác cân |
Biết các khái niệm tam giác cân. Biết các tính chất của cân. Biết vẽ cân. |
Hiểu được số đo các góc của tam giác vuông cân. |
Vận dụng tính chất tam giác cân để giải bài tập đơn giản.
|
C/minh được cân và ứng dụng vào các dạng toán khác ở mức độ khó hơn |
2. Tam giác đều |
Biết các khái niệm tam giác đều. Biết các tính chất của tam giác đều. |
Hiểu cách chứng minh một là tam giác đều. Biết được số đo các góc của đều. |
|
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5’)
H :
Hãy phát biểu ba trường hợp bằng nhau của tam giác?
Nhận dạng tam giác ở mỗi hình?
:
Hãy phát biểu ba trường hợp bằng nhau của tam giác?
Nhận dạng tam giác ở mỗi hình?
Đáp án: ABC là tam giác nhọn; EDF là tam giác vuông; HIK là tam giác tù. (10đ)
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Để phân loại các tam giác trên, người ta đã dùng yếu tố về góc. Vậy có loại tam giác đặc biệt nào mà lại sử dụng yếu tố về cạnh để xây dựng khái niệm không? Vào bài mới. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Hình thành kiến thức tam giác cân (19’)
(1) Mục tiêu: HS biết được thế nào là tam giác cân. Phát hiện ra cách vẽ, dấu hiệu nhận biết tam giác cân.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp
(4) Phương tiện dạy học: Bảng phấn, sgk, compa, ê ke.
(5) Sản phẩm: HS nắm được định nghĩa tam giác cân. Hiểu được tính chất và dấu hiệu nhận biết tam giác cân.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||||||||||||||||||||
1. Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
Â:
góc đỉnh;
AB, AC cạnh bên, BC cạnh đáy.
?1
2
?2
Chứng minh Xét ABD và ACD, Có AB = AC (gt) Â1 = Â2 (gt), AD chung Nên ABD = ACD (c.g.c)
Định lý 1: Trong một tam giác cân, hai góc ở đáy bằng nhau
ABC cân tại A
Định lý 2: Nếu một tam giác có hai góc bằng nhau thì đó là tam giác cân Định nghĩa: Sgk/126
ABC vuông cân tại A Â = 1v, AB = AC
GiảiABC có Â = 1v,
Mà ABC cân tại A
|
G em hãy đọc xem hình vẽ cho biết điều gì? GV: ABC có AB = AC đó là cân. H: Thế nào là cân? GV Hướng dẫn HS cách vẽ ABC cân tại A. Vẽ cạnh BC. Dùng compa vẽ các cung tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại A GV giới thiệu: cạnh bên, cạnh đáy, góc ở đáy, góc ở đỉnh qua ví dụ cụ thể ABC GV cho HS làm ?1 G
GV gọi 2HS lần lượt trả lời miệng bài ?1 GV yêu cầu HS giải ?2 (treo bảng phụ) Cho
ABC
cân tại A. Tia phân giác của góc A cắt BC ở D. Hãy so
sánh
H:
Qua hình vẽ dự đoán xem hai góc
Vậy 2 góc ở đáy của cân như thế nào? GV yêu cầu HS phát biểu định lý 1 Ngược lại nếu ABC có 2 góc bằng nhau thì đó có phải là cân hay không ? G
H: này có những đặc điểm gì ?
GV: ABC ở hình trên gọi là vuông cân. GV yêu cầu HS nêu định nghĩa vuông cân Yêu cầu HS giải bài ?3 (Bảng phụ) Gọi HS vẽ hình và ghi GT, KL GV
gọi 1HS lên bảng tính
GV gọi HS nhận xét |
HS: hình cho biết ABC có hai cạnh bằng nhau là cạnh AB và cạnh AC
HS: Trả lời Sgk HS: thực hiện vẽ theo sự hướng dẫn của GV
HS: đọc đề bài và quan sát hình vẽ ở bảng phụ
HS1: Các tam giác cân trên hình vẽ là ABC, ADE, CAH HS2: Kể tên cạnh, góc... HS: đọc đề và vẽ hình
HS: chứng minh
HS nêu định lý 1 Sgk
1HS: phát biểu định lý 2
HS: nghe GV giới thiệu HS: ABC ở hình vẽ có Â = 1v ; AB = AC
HS: nêu định nghĩa vuông cân Sgk/126
HS : vẽ hình và ghi GT, KL
1HS lên bảng tính
Một vài HS nhận xét |
Tư duy, giải quyết vấn đề
Tư duy, vận dụng, giao tiếp
|
HOẠT ĐỘNG 2. Hình thành kiến thức tam giác đều (10’)
(1) Mục tiêu: HS Biết được thế nào là tam giác đều. Phát hiện ra cách vẽ, tính chất, dấu hiệu nhận biết tam giác đều
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp
(4) Phương tiện dạy học: Bảng phấn, sgk, compa, ê ke.
(5) Sản phẩm: HS nắm được định nghĩa và tính chất về góc của tam giác đều.
3. Tam giác đều: Định nghĩa: T
ABC là đều
?4 a)
Do AB = AC nên
ABC cân tại A
Do AB = AC nên ABC cân
tại B
b) Từ (1) và (2) ở câu a Â
=
mà
 +
Â
=
Hệ quả: Trong 1tam giác đều, mỗi góc bằng 600. Nếu 1 tam giác có 3 góc bằng nhau thì đó là đều Nếu 1 tam giác cân có 1 góc bằng 600 thì đó là đều |
H: Nếu cạnh đáy của cân cũng bằng cạnh bên thì đó có đặc điểm gì về 3 cạnh ? GV: có 3 cạnh bằng nhau thì gọi là đều GV hướng dẫn HS vẽ đều bằng thước và compa GV cho HS làm bài ?4 (đề bài trên bảng phụ) GV gọi 1HS trình bày câu a GV có thể cho HS dự đoán số đo của mỗi góc bằng cách đo góc. Sau đó gọi 1 HS lên bảng chứng minh câu b GV chốt lại: Trong 1 tam giác đều mỗi góc bằng 600 đó chính là hq 1 H: Ngoài việc dựa vào định nghĩa để chứng minh tam giác đều, em còn có cách chứng minh nào khác không ? GV treo bảng phụ 3 hquả |
HS: 3 cạnh bằng nhau
HS: Nhắc lại thế nào là đều HS: vẽ đều dưới sự hướng dẫn của GV
HS: đọc đề bài và vẽ đều ABC HS1: trình bày câu a
HS2: trình bày câu b
HS1: Chứng minh hệ quả 2 HS2: chứng minh hệ quả 3 HS: Nhắc lại ba hệ quả |
Giải quyết vấn đề, Tư duy.
|
C. LUYỆN TẬP: Đã thực hiện ở trên
HOẠT ĐỘNG 3. Vận dụng (5’)
(1) Mục tiêu: HS biết vận dụng định nghĩa, tính chất tam giác cân, tam giác đều, tam giác vuông cân để giải bài tập đơn giản và các bài tập tổng hợp.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp
(4) Phương tiện dạy học: Bảng phấn, sgk, compa, ê ke.
(5) Sản phẩm: Bài giải của Hs.
Bài 47. Sgk/127: H.116: ABD và ACE cân tại A vì AB = AD ; AC = AE. H.117:
GIH
cân tại I vì
H.118: OMK cân (OM = KM) ONP cân tại N (ON = NP) OKP
cân tại O( OMN đều (OM = MN = NO). |
GV tổ chức cho Hs làm bài tập 47. GV gọi HS nhận xét và bổ sung.
|
HS lần lượt giải H.116, H.117, H.118
|
Tư duy, hợp tác.
|
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG:
HOẠT ĐỘNG 4. Tìm tòi và mở rộng (3’)
(1) Mục tiêu: HS biết vận dụng định nghĩa, tính chất tam giác cân, tam giác đều, tam giác vuông cân để giải quyết các tình huống thực tiễn.
(2) Phương pháp/Kĩ thuật dạy học: vấn đáp gợi mở, KT động não.
(3) Hình thức tổ chức hoạt động: Hoạt động cá nhân.
(4) Phương tiện dạy học: Sgk, mạng Internet, ...
(5) Sản phẩm: Nêu một số ứng dụng của hai tam giác cân trong đời sống.
GV giao nhiệm vụ về nhà cho các nhóm thông qua phiếu học tập. 1) Tìm hiểu qua người lớn hay mạng internet: Tại sao 2 vì kèo của mái nhà thường tạo thành tam giác cân? 2) Tìm những ứng dụng khác của các tam giác đặc biệt trong đời sống thực tiễn. 3) Đọc bài đọc thêm (Sgk/128) GV đánh giá sản phẩm và có thể cho điểm động viên nhóm làm tốt trong tiết học sau. |
HS thảo luận theo nhóm sau đó nộp lại sản phẩm bằng phiếu học tập. |
E. HƯỚNG DẪN VỀ NHÀ (2’)
Nắm vững định nghĩa và tính chất về góc của cân, vuông cân, đều. Các cách chứng minh một tam giác là cân, là đều.
Bài tập số 46; 49; 50 tr127 SGK
Bài 67; 68; 69; 70 tr106 SBT.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Làm bài tập 47.Sgk/127 (MĐ1)
Câu 2: Làm bài tập trên phiếu học tập (MĐ2, 3)
Tuần: 21 Tiết KHGD: 37 |
Ngày soạn: 14/01/2018 Ngày dạy: 15/01/2018 |
|
LUYỆN TẬP |
|
|
I. MỤC TIÊU:
1. Kiến thức: HS được củng cố các kiến thức về tam giác cân và hai dạng đặc biệt của tam giác cân. HS biết thêm các thuật ngữ: định lí thuận, định lí đảo; biết quan hệ thuận đảo của hai mệnh đề và hiểu rằng có những định lí không có định lí đảo.
2. Kĩ năng: Có kĩ năng vẽ hình và tính số đo các góc (ở đỉnh hoặc ở đáy) của một tam giác cân. Biêt chứng minh một tam giác cân; nột tam giác đều. Biết định lí thuận, định lí đảo.
3. Thái độ: Phát huy tư duy của học sinh.
4. Xác định nội dung trọng tâm của bài: Củng cố các kiến thức về tam giác cân và hai dạng đặc biệt của tam giác cân.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, sáng tạo, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác, tự học.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, compa, thước đo góc, êke, bảng phụ.
2. Học sinh: Thước thẳng, compa, thước đo góc, Sgk.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Tam giác cân. |
Biết định nghĩa, tính chất, dấu hiệu nhận biết tam giác cân |
Hiểu cách c/m tam giác cân, tam giác đều. |
Biết vận dụng kiến thức vào giải bài toán. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (7')
HS1: Nêu định nghĩa tam giác cân. Phát biểu định lí 1, 2 về tính chất của tam giác cân?
Làm bài tập 49a/127.
HS
nêu đúng ĐN được 3đ. Đúng ĐL được 3đ.
Làm
bài tập 49/127 a)
Góc ở đỉnh của tam giác cân bằng 400
![]() các góc ở đáy của tam giác cân bằng nhau và bằng:
các góc ở đáy của tam giác cân bằng nhau và bằng:
![]() (4đ)
(4đ)
HS2: Nêu định nghĩa tam giác đều? Các hệ quả? Làm bài tập 49b/127.
HS
nêu đúng ĐN được 3đ. Đúng hệ quả được 3đ. Làm
bài tập 49/127 b)
Góc ở đáy của tam giác cân bằng 400
![]() góc ở đỉnh của tam giác cân bằng 1800
– 400
. 2 = 1000
(4đ)
góc ở đỉnh của tam giác cân bằng 1800
– 400
. 2 = 1000
(4đ)
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Ở tiết học trước các em đã biết định nghĩa, tính chất của tam giác cân, tam giác đều. Tiết học hôm nay các em sẽ được luyện tập để khắc sâu hơn kiến thức đã học. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Vận dụng (30’)
(1) Mục tiêu: HS biết vận dụng định nghĩa, tính chất tam giác cân, tam giác đều, tam giác vuông cân để giải bài tập đơn giản và các bài tập tổng hợp.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng phấn, sgk, thước đo độ, thước thẳng có chia khoảng.
(5) Sản phẩm: Lời giải bài 50, 51, 52.Sgk
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||||||||
1
a)
b)
2. Bài 51.Sgk/128:
GT
AD
= AE
BD
cắt CE tại I
Kl
a)
So sánh
b) a)
Xét
AB
= AC (gt);
AD = AE (gt) Nên
Cách 2: Vì
E
Vì
D
mà AB = AC; AE = AD (gt)
-
Xét
BC cạnh chung
DC = BE (chứng minh trên) Nên
mà
b)
Ta có
Mà
Vậy
3
Xét
OA là cạnh chung Nên
Do
đó
Trong
tam giác vuông ABO có
Chứng minh tương tự có
|
GV: Đưa bảng phụ ghi đề bài 50/127 Sgk và hình vẽ 119 H:
Nếu là mái tôn, góc ở đỉnh
GV:
Tương tự hãy tính
GV: Như vậy với tam giác cân, nếu biết số đo của góc ở đỉnh thì tính được số đo của góc ở đáy. Và ngược lại biết số đo của góc ở đáy sẽ tính được sđ của góc ở đỉnh.
GV: Đưa bảng phụ ghi đề bài 51/128 Sgk
GV: Gọi 1 HS lên bảng vẽ hình và ghi GT, KL.
H:
Muốn so sánh
GV: Gọi 1 HS trình bày miệng bài chứng minh, sau đó yêu cầu 1 HS lên trình bày GV: Có thể cùng phân tích với HS cách chứng minh khác như sau:
GV: Yêu cầu HS trình bày miệng cách chứng minh này. H:
H: Nếu câu a chứng minh theo cách 1 thì câu b chứng minh như thế nào? GV: Khai thác bài toán H: Nếu nối ED, em có thể đặt thêm những câu hỏi nào? Hãy chứng minh? Cho HS hoạt động nhóm tìm câu hỏi. GV: kiểm tra các cách chứng minh của các nhóm và đánh giá việc khai thác bài toán của các nhóm.
GV: Đưa bảng phụ ghi đề bài GV: Yêu cầu cả lớp vẽ hình và gọi 1 HS lên bảng vẽ hình, ghi GT, KL của bài toán
H: Theo em tam giác ABC là tam giác gì?
GV: Hãy chứng minh dự đoán đó.
|
HS đọc đề bài.
HS
nêu cách tính góc ở đáy
HS trả lời và lên bảng làm bài.
HS: Xem đề bài bài 51/128 Sgk
Một HS lên trình bày vẽ hình và ghi GT, KL trên bảng
HS trả lời
Một HS lên trình bày trên bảng
HS trình bày miệng cách 2
-
HS trả lời
HS nghe GV khai thác bài toán.
HS hoạt động nhóm tìm câu hỏi như sau: c)
Chứng minh
d)
Chứng minh
Một HS đọc to đề bài
Cả lớp vẽ hình và ghi GT, KL của bài toán 1 HS lên bảng vẽ hình, ghi GT, KL của bài toán
- Dự đoán tam giác ABC là tam giác đều - HS chứng minh
|
Năng lực tư duy, sáng tạo, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác, tự học.
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, tự học.
|
C. LUYỆN TẬP: Đã thực hiện ở trên
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG:
HOẠT ĐỘNG 3. Tìm tòi, mở rộng (5’)
(1) Mục tiêu: HS biết vận dụng định nghĩa, tính chất tam giác cân, tam giác đều, tam giác vuông cân để giải quyết các tình huống thực tiễn. Hình thành năng lực ứng dụng CNTT, tự nghiên cứu, quan sát, tổng hợp, …
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, KT động não.
(3) Hình thức tổ chức hoạt động: Hoạt động cá nhân.
(4) Phương tiện dạy học: Sgk, trên mạng Internet
(5) Sản phẩm: Kết quả tìm hiểu của các nhóm về ứng dụng của các tam giác đặc biệt trong đời sống thực tế.
GV: Chuyển giao nhiệm vụ học tập. 1) GV: Đưa bảng phụ ghi mục “Bài đọc thêm” 2) Tìm những ứng dụng của các tam giác đặc biệt trong đời sống thực tế? GV giao nhiệm vụ về nhà cho các nhóm thông qua phiếu học tập. GV đánh giá sản phẩm và có thể cho điểm động viên nhóm làm tốt trong tiết học sau. |
HS đọc mục “Bài đọc thêm” HS thảo luận theo nhóm sau đó nộp lại sản phẩm bằng phiếu học tập. Hs có thể về nhà làm việc theo nhóm để hoàn thành nội dung phiếu học tập. |
E. HƯỚNG DẪN VỀ NHÀ (2’)
- Ôn lại định nghĩa và tính chất tam giác cân, tam giác đều. Cách c/minh một tam giác là tam giác cân, tam giác đều.
- Làm bài 72, 73.SBT/107
- Đọc trước bài “ Định lí Py-ta-go”
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Hãy nêu định nghĩa và tính chất tam giác cân, tam giác đều. (MĐ1)
Câu 2: Nêu cách chứng minh một tam giác là tam giác cân, tam giác đều. Xem và tự giải lại các bài tập đã luyện tập. (MĐ2, 3)
Tuần: 21 Tiết KHGD: 38 |
Ngày soạn: 14/01/2018 Ngày dạy: 17/01/2018 |
|
§7. ĐỊNH LÍ PY-TA-GO |
|
|
I. MỤC TIÊU:
1. Kiến thức: Học sinh nắm được định lí Py-ta-go về quan hệ giữa ba cạnh của một tam giác vuông và định lí py-ta-go đảo.
2. Kĩ năng: Biết vận dụng định lí Py-ta-go để tính độ dài một cạnh của tam giác vuông khi biết độ dài hai cạnh kia. Biết vận dụng định lí Py-ta-go đảo để nhận biết một tam giác là tam giác vuông.
3. Thái độ: Biết vận dụng kiến thức học trong bài vào thực tế.
4. Xác định nội dung trọng tâm của bài: Nắm vững định lí Py-ta-go về quan hệ giữa ba cạnh của một tam giác vuông và định lí py-tago đảo để nhận biết tam giác vuông. Bước đầu biết vận dụng giải bài tập.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác, tự học.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ ghi đề bài tập, định lí Py-ta-go (thuận, đảo), bài giải một số bài tập. Hai tấm bìa màu hình vuông có cạnh bằng a + b và tám tờ giấy trắng hình tam giác vuông bằng nhau, có độ dài hai cạnh góc vuông là a và b.
2. Học sinh: Đọc bài đọc thêm giới thiệu định lí thuận, đảo. Thước thẳng, êke, compa, máy tính bỏ túi.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Định lí Py-ta-go. |
Biết phát biểu định lí Py-ta-go. |
|
Biết vận dụng định lí Py-ta-go vào giải bài toán tính cạnh của tam giác vuông. |
|
2. Định lí Py-ta-go đảo. |
Biết phát biểu định lí Py-ta-go đảo. |
Biết kiểm tra bộ ba số tạo thành một tam giác vuông hay không. |
|
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: Không
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (2’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Giới thiệu về nhà toán học Py-ta-go: Py-ta-go sinh trưởng trong một gia đình quí tộc ở đảo Xa-mốt, một đảo giàu có ở ven biển Ê-giê thuộc Địa trung Hải. Ông sống trong khoảng năm 570 đến năm 500 trước công nguyên. Từ nhỏ, Py-ta-go đã nổi tiếng về trí thông minh khác thường. Ông đã đi nhiều nơi trên thế giới và trở nên uyên bác trong hầu hết các lĩnh vực quan trọng: số học, hình học, thiên văn, địa lí, âm nhạc, yhọc, triết học. Một trong những công trình nổi tiếng của ông là hệ thức giữa độ dài các cạnh của tam giác vuông, đó chính là định lí Py-ta-go mà hôm nay chúng ta học. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Định lí Py-ta-go. (20’)
(1) Mục tiêu: Học sinh nắm được định lý py-ta-go
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, thước, êke.
(5) Sản phẩm: Học sinh biết cách biểu diễn định lý py-ta-go dưới dạng hình vẽ và tóm tắt dưới dạng GT, KL. Có kĩ năng sử dụng định lý py-ta-go để tính cạnh góc vuông chưa biết
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1. Định lí Pytago: ? Cạnh huyền.
A C
?2
a) Diện tích phần hình vuông bị gạch chéo là c2 b) Diện tích hai hình vuông bị gạch chéo là a2 + b2 c) c2 = a2 + b2
*
=> BC2 = AB2 + AC2 ?3 a) ABC vuông tại B nên AB2 + BC2 = AC2 hay AB2 + 82 = 102 AB2 = 102 – 82 = 36 = 62 x = AB = 6 b) DEF vuông tại D nên ta có: DE2 + DF2 = EF2 hay 12 + 12 = EF2 EF2 = 1 + 1 = 2
x
= EF =
|
Cho
học
sinh
làm
GV gọi 1 HS lên bảng vẽ (sử dụng quy ước 1cm trên bảng) H: Hãy cho biết độ dài cạnh huyền của tam giác vuông? - Các độ dài 3, 4, 5 có mối quan hệ gì? -Thực
hiện
GV: Đưa bảng phụ có dán sẵn hai tầm bìa màu hình vuông có cạnh (a + b) - Yêu cầu HS xem Sgk/129, H.121và H.122 sau đó mời 4 HS lên bảng ghép hình. - Ở hình 121, phần bìa không bị che lấp là một hình vuông có cạnh bằng c, hãy tính diện tích phần bìa đó theo c? - Ở hình 122, phần bìa không bị che lấp gồm hai hình vuông có cạnh là a và b, hãy tính diện tích phần bìa đó theo a và b? H: Có nhận xét gì về diện tích phần bìa không bị che lấp ở hai hình? Giải thích?
- Từ đó rút ra nhận xét gì về quan hệ giữa c2 và a2 + b2? H: Hệ thức c2 = a2 +b2 nói lên điều gì về quan hệ 3 cạnh của tam giác vuông? GV: Đó chính là nội dung định lí Pytago. Gọi Hs lên bảng ghi định lí dưới dạng ký hiệu? H:
Từ đó AB2 = ?; AC2 = ? - Đọc phần lưu ý Sgk/130 -
Yêu cầu HS làm
H: Kết quả tìm được bằng bao nhiêu?
|
HS
làm
HS: Cả lớp vẽ hình vào vở Một HS lên bảng vẽ HS: độ dài cạnh huyền của tam giác vuông là 5cm.
-
Thực hiện
- HS xem Sgk/129, hình 121 và hình 122,
HS lên bảng.
HS: diện tích phần bìa đó bằng c2.
HS: diện tích phần bìa đó bằng a+b2
HS: Diện tích phần bìakhông bị che lấp ở hai hình bằng nhau vì đều bằng diện tích hình vuông trừ đi diện tích 4 tam giác vuông HS: Vậy c2 = a2 + b2 HS: Hệ thức này cho biết trong tam giác vuông, bình phương độ dài cạnh huyền bằng tổng các bình phương độ dài hai cạnh góc vuông. - Vài HS đọc to định lí Pytago
HS: Trả lời.
- Đọc phần lưu ý Sgk
HS: Vận dụng làm ?3
HS: trình bày miệng
|
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, tự học.
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, tự học.
|
HOẠT ĐỘNG 3. Định lí Py-ta-go đảo. (11’)
(1) Mục tiêu: HS nắm được định lý py-ta-go đảo. Nhận biết tam giác là tam giác vuông.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, ê ke.
(5) Sản phẩm: Học sinh hiểu được định lý py-ta-go đảo
2. Định lí Py-ta-go đảo: ?4. Vẽ tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm.
Đ
|
-
Cho HS
làm
- Hãy dùng thước đo góc xác định số đo góc của góc BAC. H: Có nhận xét gì về tam giác nếu bình phương độ dài một cạnh bằng tổng bình phương hai cạnh kia? GV: Người ta đã chứng minh được định lí Pytago đảo. |
-
HS làm
- Cả lớp vẽ hình vào vở - Một HS thực hiện trên bảng -
(vì
32
+42
= 52
= 25), bằng đo đạc ta thấy
HS: Đọc định lí đảo Sgk/130
|
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, tự học.
|
C. LUYỆN TẬP
HOẠT ĐỘNG 3. Vận dụng (7’)
(1) Mục tiêu: HS biết vận dụng định lý py-ta-go để giải bài tập đơn giản.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk.
(5) Sản phẩm: Bài giải của Hs.
Bài tập 53.Sgk/131 a)
b)
Kết quả c) Kết quả x = 20 d) Kết quả x =13 Bài tập a) Có 62 +82 = 100 = 102 Vậy tam giác có ba cạnh là 6cm, 8cm, 10cm là tam giác vuông. b)
|
- Cho HS làm bài tập 53 Sgk theo nhóm Đưa bảng phụ ghi đề bài Yêu cầu đại diện hai nhóm trình bày bài Gv kiểm tra bài của vài nhóm - Nêu bài tập: Cho tam giác có độ dài ba cạnh là a) 6cm, 8cm, 10cm. b) 4cm, 5cm, 6cm. tam giác nào là tam giác vuông? Vì sao?
|
HS làm bài tập 53 Sgk theo nhóm Đưa bảng phụ ghi đề bài - HS hoạt động nhóm: Đại diện hai nhóm trình bày bài HS cả lớp nhận xét - HS nghe GV nêu bài tập, theo dõi trả lời.
|
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác, tự học.
|
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG:
HOẠT ĐỘNG 4. Tìm tòi và mở rộng (3’)
(1) Mục tiêu: HS biết vận dụng định nghĩa, tính chất tam giác cân, tam giác đều, tam giác vuông cân để giải quyết các tình huống thực tiễn.
(2) Phương pháp/Kĩ thuật dạy học: vấn đáp gợi mở, KT động não.
(3) Hình thức tổ chức hoạt động: Hoạt động cá nhân.
(4) Phương tiện dạy học: Sgk, mạng Internet, ...
(5) Sản phẩm: Hiểu biết của HS về ứng dụng của tam giác vuông trong đời sống.
- Đọc mục có thể em chưa biết” Sgk/132 - Tìm hiều cách kiểm tra góc vuông của người thợ xây dựng (thợ nề, thợ mộc) |
HS thảo luận theo nhóm sau đó nộp lại sản phẩm bằng phiếu học tập. |
E. HƯỚNG DẪN VỀ NHÀ (2’)
- Học thuộc định lí Py-ta-go (thuận và đảo)
- BTVN: 55, 56, 57, 68/ 131, 132 Sgk; 82, 82, 86/ 108 SBT.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Phát biểu định lí Pytago thuận, đảo. So sánh hai định lí này. (MĐ1)
Câu 2: Cho HS làm bài tập và bài 53 Sgk. (MĐ2, 3)
Tuần: 21 Tiết KHGD: 39 |
Ngày soạn: 14/01/2018 Ngày dạy: 18/01/2018 |
|
LUYỆN TẬP |
|
|
I. MỤC TIÊU:
1. Kiến thức: Củng cố định lí Py-ta-go và định lí Py-ta-go đảo.
2. Kĩ năng: Vận dụng định lí Py-ta-go để tính độ dài một cạnh của tam giác vuông và vận dụng định lí Py-ta-go đảo để nhận biết một tam giác vuông.
3. Thái độ: Hiểu và vận dụng kiến thức học trong bài và thực tế.
4. Xác định nội dung trọng tâm của bài: Nắm vững định lí Py-ta-go về quan hệ giữa ba cạnh của một tam giác vuông và định lí Py-ta-go đảo để nhận biết tam giác vuông. Bước đầu biết vận dụng giải bài tập.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác, tự học.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ, một sợi dây thắt nút thành 12 đoạn bằng nhau. Thước thẳng, êke, compa.
2. Học sinh: Học và làm bài ở nhà. Đọc mục có thể em chưa biết. Thước thẳng, êke, compa.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Định lí Py-ta-go. |
Biết phát biểu định lí Py-ta-go. |
|
Biết vận dụng định lí Py-ta-go vào giải bài toán tính cạnh của tam giác vuông. |
|
2. Định lí Py-ta-go đảo. |
Biết phát biểu định lí Py-ta-go đảo. |
Biết kiểm tra bộ ba số tạo thành một tam giác vuông hay không. |
Vận dụng chứng minh hai tam giác bằng nhau để giải các bài toán liên quan. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (10')
H: Phát biểu định lí Pytago. Vẽ hình và viết hệ thức minh họa.
Chữa bài tập 55.Sgk/131
Đáp án:
Đ ịnh
lí Pytago:
Trong
tam
giác
vuông, bình phương độ dài cạnh huyền bằng tổng các
bình phương độ dài hai cạnh góc
vuông.………………………………………………. 4đ
ịnh
lí Pytago:
Trong
tam
giác
vuông, bình phương độ dài cạnh huyền bằng tổng các
bình phương độ dài hai cạnh góc
vuông.………………………………………………. 4đ
![]() ABC
có
ABC
có
![]()
![]()
 BC2
= AB2
+
AC2
...............………………………………………. 2đ
BC2
= AB2
+
AC2
...............………………………………………. 2đ
Chữa bài tập 55.Sgk
AC2 = BC2 - AB2 = 42 - 12 = 16 – 1 = 15…………………………………. 3đ
![]() …………………………………………………. 1đ
…………………………………………………. 1đ
GV nhận xét, cho điểm
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Tiết trước các em đã được học định lí Py-ta-go về quan hệ giữa ba cạnh của một tam giác vuông và định lí Py-ta-go đảo để nhận biết tam giác vuông. Hôm nay, chúng ta sẽ vận dụng định lí Py-ta-go để tính độ dài một cạnh của tam giác vuông và vận dụng định lí Py-ta-go đảo để nhận biết một tam giác vuông |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Luyện tập (27’)
(1) Mục tiêu: HS vận dụng định lí Py-ta-go để tính độ dài một cạnh của tam giác vuông và vận dụng định lí Py-ta-go đảo để nhận biết một tam giác vuông.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, thước thẳng, êke, ...
(5) Sản phẩm: Bài làm của học sinh.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||||
1. Bài 57.Sgk/131: Lời giải của bạn Tâm là sai. Ta phải so sánh bình phương của cạnh lớn nhất với tổng bình phương hai cạnh còn lại.
2
Tam giác vuông ABD, có: BD2 = AB2 + AD2 (đl Pytago) Hay BD2 = 52 + 102 = 125
3
Ta
có
AB2 = AO2 + OB2 (đl Pytago) AO
= OC +
Tính tương tự, ta có: BC = CD = DA = AB = 10cm 4
Gọi đường chéo của tủ là d Ta có d2 = 202 + 42(đl Pytago) d2 = 400 + 16 = 416
Chiều cao của nhà là 21 dm
|
GV: Đưa bảng phụ ghi đề bài 57. H:
GV: Tính đường chéo của một mặt bàn hình chữ nhật có chiều dài 10dm, chiều rộng 5dm. H: Nêu cách tính đường chéo của mặt bàn hình chữ nhật?
GV: Đưa bảng phụ ghi đề bài 87 GV: Yêu cầu một HS lrên bảng vẽ hình và ghi GT, KL
- Hãy nêu cách tính độ dài AB?
GV: Yêu cầu HS hoạt động nhóm. (Đưa bảng phụ ghi đề bài) Gọi đại diện một nhóm trình bày lời giải GV: Nhận xét việc hoạt động của các nhóm và bài làm. |
HS:
Trong ba cạnh, cạnh AC = 17 là cạnh lớn nhất. Vậy
HS: Đọc đề bài, vẽ hình.
HS nêu cách tính.
HS đọc đề trên bảng phụ. 1 HS lên bảng vẽ hình và ghi GT, KL HS cả lớp vẽ hình vào vở HS: Nêu cách tính độ dài AB.
HS hoạt động nhóm
Đại diện một nhóm trình bày lời giải HS lớp nhận xét, góp ý.
|
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác, tự học.
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác, tự học.
|
C. LUYỆN TẬP: Đã thực hiện ở trên
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG: Đã thực hiện ở trên
HOẠT ĐỘNG 3. Tìm tòi, mở rộng (5’)
(1) Mục tiêu: Tạo cho Hs nhu cầu tìm hiểu ứng dụng của tam giác vuông trong đời sống.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, KT động não.
(3) Hình thức tổ chức hoạt động: Hoạt động cá nhân.
(4) Phương tiện dạy học: Sgk
(5) Sản phẩm: K.quả tìm hiểu của các nhóm về ứng dụng của tam giác vuông trong đời sống.
GV: Đưa bảng phụ giới thiệu mục “Có thể em chưa biết” H: Các bác thợ nề, thợ mộc kiểm tra góc vuông như thế nào? GV: Đưa bảng phụ vẽ hình 131, 132 Sgk. Dùng sợi dây có thắt nút 12 đoạn bằng nhau và êke gỗ có tỉ lệ cạnh là 3, 4, 5 để mimh họa cụ thể . GV: Đưa tiếp hình 133 và trình bày như Sgk. GV: Đưa thêm hình phản ví dụ GV: Yêu cầu HS nhận xét. - Đọc mục “Có thể em chưa biết”; “Ghép hai hình vuông thành một hình vuông” Sgk/134. Theo hướng dẫn của Sgk, hãy thực hiện cắt ghép từ hai hình vuông thành một hình vuông. |
H
HS quan sát GV hướng dẫn HS nêu nhận xét: +
Nếu AB = 3, AC = 4, BC = 5 thì
+
Nếu AB = 3, AC = 4, BC < 5 thì
+
Nếu AB = 3, AC = 4, BC > 5 thì
HS: Lắng nghe |
Tư duy, giải quyết vấn đề,
vận dụng, giao tiếp, làm chủ bản thân, tự học.
|
E. HƯỚNG DẪN VỀ NHÀ (2’)
- Ôn tập định lí Py-ta-go (thuận, đảo)
- Làm bài tập: 59, 60, 61.Sgk/133. Tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Hãy phát biểu định lí Py-ta-go thuận, định lí Py-ta-go đảo. (MĐ1)
Câu 2: Làm bài tập 59, 60, 61.Sgk/133 (MĐ3)
Tuần: 22 Tiết KHGD: 41 |
Ngày soạn: 20/01/2018 Ngày dạy: 22/01/2018 |
|
LUYỆN TẬP (tt) |
|
|
I. MỤC TIÊU:
1. Kiến thức: Tiếp tục củng cố định lí Py-ta-go. Vận dụng định lí Py-ta-go để giải bài tập và một số tình huống thực tế.
2. Kĩ năng: Có kỹ năng vẽ hình và tính số đo cạnh của tam giác vuông khi biết hai cạnh.
3. Thái độ: Giáo dục tính cẩn thận, chính xác, óc tư duy sáng tạo.
4. Xác định nội dung trọng tâm của bài: Củng cố định lý Py-ta-go và định lý đảo “Bộ ba số py-ta-go”.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Sgk, SBT, giáo án, bảng phụ, đồ dùng giảng dạy.
2. Học sinh: Sgk, chuẩn bị bài ở nhà, dụng cụ học tập.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Định lí Py-ta-go. |
Biết phát biểu định lí Py-ta-go. |
|
Biết vận dụng định lí Py-ta-go vào giải bài toán tính cạnh của tam giác vuông. |
|
2. Định lí Py-ta-go đảo. |
Biết bộ ba số tạo thành một tam giác vuông. |
|
Vận dụng chứng minh hai tam giác bằng nhau để giải các bài toán liên quan. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: Lồng ghép trong luyện tập
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Tiết trước chúng ta đã luyện tập củng cố định lí Py-ta-go về quan hệ giữa ba cạnh của một tam giác vuông và định lí Py-ta-go đảo để nhận biết tam giác vuông. Hôm nay, ta sẽ tiếp tục vận dụng định lí Py-ta-go để tính độ dài một cạnh của tam giác vuông và vận dụng định lí Py-ta-go đảo để nhận biết một tam giác vuông. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Vận dụng (27’)
(1) Mục tiêu: HS biết tính độ dài các cạnh của tam giác vuông.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Bài làm của HS.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1
AC2
= DA2
+ DC2
= 482
+ 362
= 3600
2) Bài tập 60/133 sgk:
AC2
= HA2
+ HC2
= 122
+ 162
= 400
BH2
= BA2
– HA2
=
132
– 122
= 25
Do đó BC = BH + HC = 5 + 16 = 21 (cm) 3) Bài tập 61/133 sgk:
Áp dụng định lí Pytago, với: +
=
25
+ AB2 = AE2 + BE2 = 22 + 12 =
5
+
BC2 = CF2 + FB2 = 52 + 32 =
34
Vậy
4) Bài tập 62/133 sgk:
Ta có: OA2 = 42 + 32 = 25
OB2 = 62 + 42 = 52
OD2 = 82 + 32 = 73
Vậy con cún đến được vị trí A, B, D nhưng không đến được vị trí C. |
Chuyển giao: chia lớp thành 4 nhóm, giáo viên giao nhiệm vụ GV: Sử dụng đề bài trên bảng phụ, gọi HS đọc đề bài tập 59/133 sgk Btoán cho biết gì và y/c gì? GV: Nếu không có nẹp chéo ACthì khung ABCD sẽ ntn? GV: Nhận xét xử lý kq.
GV: Gọi HS đọc đề bài tập 60/133 sgk. - Độ dài đoạn AC được tính như thế nào? - Độ dài đoạn BC = ? - Để tính độ dài đoạn BC ta phải tính độ dài đoạn nào ?
Một HS đọc đề bài tập 61/133 sgk . GV treo hình 135 lên bảng.
-
Làm thế nào để tính độ dài các cạch của
Một HS đọc đề bài tập 62/133 sgk. GV vẽ hình 136 lên bảng. - Để biết con cún có thể đến các vị trí A, B, C, D để canh giữ mảnh vườn hay không , ta phải làm thế nào ?
|
HS hoạt động nhóm làm bài. Thực hiện: các nhóm thảo luận, trao đổi dưới sự giúp đỡ của Gv. HS: Đại diện nhóm báo cáo thảo luận HS: Các nhóm đánh giá, nhận xét, tổng hợp
HS: Lên bảng vẽ hình. HS: Trả lời theo gợi ý
Một HS lên bảng làm, HS còn lại làm nhóm và nhận xét.
HS: Đọc bài, quan sát hình vẽ trên bảng phụ
HS1: Lên bảng tính độ dài cạch AB. HS2: Lên bảng tính độ dài cạnh BC. HS3: Lên bảng tính độ dài cạnh AC. HS còn lại làm và nhận xét.
HS: Trả lời. HS: Lên bảng làm, HS còn lại làm và nhận xét.
|
Năng lực tự học, tính toán, sử dụng ngôn ngữ toán học và sử dụng các công thức tổng quát.
Năng lực tự học, tính toán, sử dụng ngôn ngữ toán học và sử dụng các công thức tổng quát.
|
C. LUYỆN TẬP: Đã thực hiện ở trên
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG: Kiểm tra 15’
B ài
1:
(3,0 điểm)
Cho tam giác ABC có độ AB = 6cm, AC = 8cm, BC = 10cm. Tam giác
ABC có phải là tam giác vuông không? Giải thích tại sao?
ài
1:
(3,0 điểm)
Cho tam giác ABC có độ AB = 6cm, AC = 8cm, BC = 10cm. Tam giác
ABC có phải là tam giác vuông không? Giải thích tại sao?
Bài 2: (3,0 điểm)
Tính độ dài x trên hình vẽ bên?
Bài 3: (4,0 điểm)
Cho ∆ABC cân tại A, trên hai cạnh AB và AC
lần lượt lấy hai điểm M và N sao cho AM = AN,
kẻ
AH
![]() BC (H
BC (H
![]() BC).
BC).
a) Chứng minh ∆ABH = ∆ACH
b) Chứng minh BN = CM
c) Gọi AH cắt MN tại I. Chứng minh IM = IN.
Bài |
Câu |
Đáp án |
Điểm |
Bài 1 (3,0 điểm) |
|
Ta có: 102 = 100; 63 + 82 = 100
Do đó ABC vuông tại A (định lí py- ta- go đảo) |
1,0 1,0 1,0 |
Bài 2 (3,0 điểm) |
|
∆ABC vuông tại A. Theo định lí py-ta-go, ta có: BC2 = AB2 + AC2 Hay x2 = 32 + 42 x2
= 25
|
0,5 1,0 1,0 0,5 |
Bài 4 (4,0 điểm)
|
|
Vẽ
hình
|
0,5 |
a |
Xét ∆ABH và ∆ACH, có: AB = AC(gt)
AH: cạnh chung Do đó ∆ABH = ∆ACH (cạnh huyền-cgv) |
1,0 |
|
b |
Xét ∆ABN và ∆ACM, có: AN = AM(gt)
AB = AC(gt) Do đó ∆ABN = ∆ACM (c.g.c)
|
1,0 0,5 |
|
c |
Vì
∆ABH = ∆ACH Nên
Xét ∆AIN và ∆AIM, có: AN
= AM (gt);
Do đó ∆AIN = ∆AIM (c.g.c) Nên IN = IM (cạnh tương ứng) |
0,5 0,5 |
E. HƯỚNG DẪN VỀ NHÀ (2’)
- Ôn lại định lí Pytago, các trường hợp bằng nhau của hai tam giác.
- Làm bài tập: 83; 84; 85; 87; 88; 89; 91/108 – 109 sbt.
- Xem trước bài mới “Các trường hợp bằng nhau của tam giác vuông”
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Hãy phát biểu định lí Py-ta-go thuận, định lí Py-ta-go đảo. (MĐ1)
Câu 2: Làm bài tập kiểm tra (MĐ3)
Tuần: 22 Tiết KHGD: 41 |
Ngày soạn: 21/01/2018 Ngày dạy: 24/01/2018 |
|
§8. CÁC TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC VUÔNG |
|
|
I. MỤC TIÊU:
1. Kiến thức: HS nắm được các trường hợp bằng nhau của hai tam giác vuông. Biết vận dụng định lý Pytago để chứng minh trường hợp cạnh huyền cạnh góc vuông của 2 vuông. Biết vận dụng các trường hợp bằng nhau của 2 vuông để chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau.
2. Kĩ năng: Tiếp tục rèn luyện khả năng phân tích tìm cách giải và trình bày bài toán chứng minh hình học.
3. Thái độ: Hiểu và vận dụng kiến thức học được vào một số bài toán thực tế.
4. Xác định nội dung trọng tâm của bài: Nắm được các trường hợp bằng nhau của hai tam giác vuông.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, êke, compa, bảng phụ ghi sẵn bài tập và câu hỏi.
2. Học sinh: Sgk, thước thẳng, êke, compa.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Các trường hợp bằng nhau của tam giác vuông. |
|
Hiểu định lí Py ta go để chứng minh tam giác vuông bằng nhau. |
Vận dụng định lí Pytago vào giải bài toán tính cạnh của tam giác vuông và một số bài toán thực tế. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (8’)
HS1: Hãy nêu ra các trường hợp bằng nhau của vuông được suy ra từ các trường hợp bằng nhau của ?
Đáp án: Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kai thì hai tam giác vuông đó bằng nhau. Hệ quả 1 và 2. Sgk/122 (10đ)
H
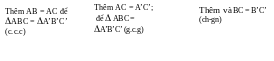
Đáp án: (10đ)
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Như vậy hai tam giác vuông bằng nhau khi chúng có những yếu tố nào bằng nhau? Vào bài mới. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Các trường hợp bằng nhau đã biết của tam giác vuông (6’)
(1) Mục tiêu: Thông qua bài tập học sinh phát hiện ra trường hợp bằng nhau khác của hai tam giác vuông
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Giải bài tập và trả lời được các câu hỏi
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1) Các trường hợp bằng nhau đã biết của tam giác vuông. Hai tam giác vuông bằng nhau khi có: 1. Hai cạnh góc vuông bằng nhau 2. Một cạnh góc vuông và một góc nhọn kề cạnh ấy bằng nhau 3. Cạnh huyền và một góc nhọn bằng nhau |
H: 2 vuông bằng nhau khi chúng có những yếu tố nào bằng nhau? G
H
Có các vuông nào bằng nhau ? Vì sao ? |
HS: Phát biểu các trường hợp bằng nhau. HS: trả lời H.143 có: AHB = AHC (c.gc) H.144 có: DKE = DKF (g.c.g) H.145 có: OMI = ONI (ch-gn) |
Năng lực giải quyết vấn đề
|
HOẠT ĐỘNG 2. Trường hợp bằng nhau về cạnh huyền và cạnh góc vuông (15’)
(1) Mục tiêu: Học sinh nắm được trường hợp bằng nhau đặc biệt của tam giác vuông.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Học sinh làm được các bài tập và trả lời được các câu hỏi và rút ra được trường hợp bằng nhau đặc biệt của tam giác vuông.
2) Trường hợp bằng nhau về cạnh huyền và cạnh góc vuông.
Đ
ABC (Â =1v), GT
DEF( BC = EF, AC = DF KL ABC = DEF Chứng minh: Xét ABC (Â =1v) AB2 = BC2 AC2 (1) Xét
DEF
( DE2 = EF2 DF2 (2) Mà AC = DF, AB = DE (3) Từ (1), (2) và (3) suy ra : AB2 = DE2 nên AB = DE Do đó ABC = DEF(c.c.c) Bài ?1 C1: Xét 2 vuông AHB và AHC, có : AB = AC (2 cạnh huyền) AH chung (cạnh góc vuông) AHB = AHC (ch-cgv) C2
: ABC
cân
AHB = AHC (ch-gn) vì
có AB = AC;
|
GV yêu cầu HS đọc nội dung trong khung Sgk/135 Cả lớp vẽ hình và ghi GT, KL của định lý GV: Gọi 1HS phát biểu định lý Pytago H: Định lý Pytago có ứng dụng gì ?
H: Vậy nhờ định lý Pytago ta có thể tính cạnh AB theo cạnh BC, AC như thế nào? Tương tự DE ? GV: Như vậy nhờ định lý Pytago ta đã chỉ ra được ABC và DEF có ba cặp cạnh bằng nhau GV gọi HS phát biểu lại trường hợp bằng nhau cạnh huyền, cạnh góc vuông của tam giác vuông
Cho HS làm bài ?2 Sgk (treo bảng phụ)
AH
C/m rằng: AHB = AHC (bằng 2 cách) GV gọi HS nêu GT, KL và 2HS lên bảng giải |
HS : đọc phần đóng khung Sgk/135 Cả lớp vẽ hình và ghi GT, KL HS: Phát biểu
HS: Khi biết hai cạnh của vuông, ta có thể tính được cạnh thứ ba của nó. HS: Lên bảng áp dụng định lý Pytago tính AB và DE Chứng minh 2 bằng nhau (c.c.c)
HS: Nhắc lại định lý
HS: đọc đề và quan sát hình 147 và ghi GT, KL ABCcân tại A GT
AH
KL AHB = AHC
HS1: cách 1 HS2: cách 2 |
Năng lực tư duy, giải quyết vấn đề, vận dụng.
|
C. LUYỆN TẬP
HOẠT ĐỘNG 3. Luyện tập (13’)
(1) Mục tiêu: Học sinh được khắc sâu về kiến thức các trường hợp bằng nhau của tam giác vuông, rèn kỹ năng về vẽ hình, viết giả thiết kết luận thông qua bài tập và dùng kiến thức lý thuyết đã được học ở trên để giải các bài tập liên quan.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Bài làm của học sinh.
*Bài 66.Sgk/137 ABC; AM pg, tt, đc GT
MD
KL Chỉ ra các bằng nhau
ADM = AEM (ch-gn) DBM = ECM (ch-gn) AMB = AMC (c.c.c)
* Chứng minhXét AHB và AHC, có:
AB = AC (gt) Nên AHB = AHC (ch-cgv) HB = HC (cạnh t/ứng) BÂH = CÂH (góc tương ứng) |
GV treo bảng phụ bài 66 G
H: Trên hình có những nào bằng nhau? GV gọi HS nhận xét Bài 63.Sgk/136 (bảng phụ) GV yêu cầu HS lên bảng ghi GT, KL GV cho HS suy nghĩ chứng minh trong 3 phút. Sau đó yêu cầu HS chứng minh miệng. GV ghi bảng
GV gọi HS nhận xét |
HS: quan sát bảng phụ 1HS lên bảng giải
HS: cả lớp làm vào nháp
HS: nhận xét 1HS lên bảng ghi GT; KL
1 HS chứng minh miệng
HS: Nhận xét |
Năng lực tư duy, vận dụng, giao tiếp, làm chủ bản thân. |
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG
Bài tập: Cho tam giác ABC, các tia phân giác của góc B và góc C cắt nhau tại I. Chứng minh rằng AI là tia phân giác của góc A.
HD: Từ I kẻ các đường vuông góc với các cạnh của tam giác ABC.
E. HƯỚNG DẪN VỀ NHÀ (2’)
Học thuộc, hiểu, phát biểu chính xác các trừơng hợp bằng nhau của vuông
Bài tập về nhà 64; 65 Sgk/136+137. Tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Bài 66 tr137 Sgk (MĐ2)
Bài 63 tr136 Sgk (MĐ3)
Tuần: 22 Tiết KHGD: 42 |
Ngày soạn: 21/01/2018 Ngày dạy: 25/01/2018 |
|
LUYỆN TẬP |
|
|
I. MỤC TIÊU:
1. Kiến thức: Củng cố kiến thức về các trường hợp bằng nhau của tam giác vuông.
2. Kĩ năng: Rèn kỹ năng chứng minh tam giác vuông bằng nhau. Kỹ năng trình bày bài chứng minh hình.
3. Thái độ: Phát huy trí lực của HS.
4. Xác định nội dung trọng tâm của bài: Củng cố kiến thức về các trường hợp bằng nhau của tam giác vuông.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân, hợp tác.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, êke, compa, bảng phụ ghi sẵn bài tập và câu hỏi.
2. Học sinh: Sgk, thước thẳng, êke, compa.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Các trường hợp bằng nhau của tam giác vuông.
|
Biết các trường hợp bằng nhau của tam giác vuông. |
|
Vận dụng các trường hợp bằng nhau của tam giác vuông để chứng minh các cạnh, các góc bằng nhau và một số bài toán liên quan. |
|
I
* Kiểm tra bài cũ: (6’)
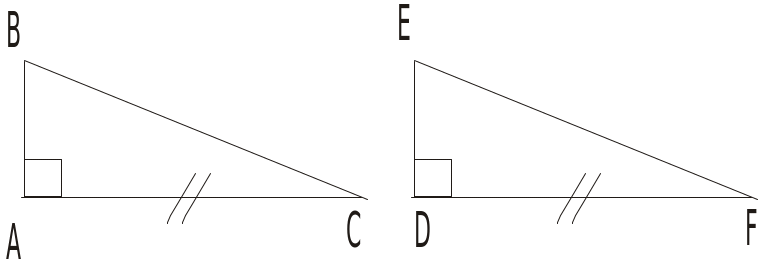
HS1: Phát biểu các trường hợp bằng nhau của tam giác vuông? (4đ)
Chữa bài tập 64 tr136 Sgk (6đ)
Đáp
án:
ABC
và DEF
có: Â =
![]() =
1v ; AC = DF
=
1v ; AC = DF
bổ
sung thêm BC = EF hoặc AB = DE Hoặc Ê =
![]() thì ABC
= DEF.
thì ABC
= DEF.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở / Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Các em đã biết các trường hợp bằng nhau của hai vuông. Hôm nay, chúng ta sẽ luyện kĩ năng chứng minh hai vuông bằng nhau và vận dụng để giải một số bài toán liên quan. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Luyện tập (36’)
(1) Mục tiêu: Học sinh được khắc sâu về kiến thức các trường hợp bằng nhau của tam giác vuông, rèn kỹ năng về vẽ hình, viết giả thiết kết luận thông qua 3 bài tập và dùng kiến thức lý thuyết đã được học ở trên để giải các bài tập liên quan.
Hs được rèn luyện về tính tự giác, tự chủ trong học tập, tạo hứng thú và yêu thích môn học, thông hiểu dạng kiến thức được cung cấp trong bài để chuẩn bị cho những tiết học thực hành
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Giải bài tập và trả lời được các câu hỏi
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1

|
Bài 65 tr 137 Sgk (treo bảng phụ)
H: Để c/m AH = AK em làm thế nào? Hãy trình bày cách giảiGV gọi 1HS lên bảng giảiGV gọi HS nhận xét câu a
H: Hãy nêu hướng chứng minh AI là phân giác của Â
GV gọi HS nhận xét và sửa saiBài 98 tr 110 SBT(Treo bảng phụ) GV hướng dẫn HS vẽ hình
H: Để chứng minh ABC cân ta cần chứng minh điều gì ?
H:
trên hình đã có 2
nào chứa 2 cạnh AB, AC (hoặc
GV: hãy tạo ra những đường phụ để tạo ra 2 vuông trên hình vẽ chứa Â1 và Â2 mà chúng đủ điều kiện bằng nhau. H: Qua bài tập này hãy cho biết một có những điều kiện gì thì là cân GV chỉnh sửa nêu thành chú ý cho HS ghi vở
Bài 101 tr 110 SBT(treo bảng phụ) GV gọi HS đọc đề GV gọi HS vẽ hình và nêu GT, KL
H: Quan sát hình vẽ em nhận thấy có những cặp vuông nào bằng nhau ?
H: Để c/minh BH = CK ta làm thế nào ?
|
HS: Đọc đề trên bảng phụ, vẽ hình và ghi GT, KL
1HS lên bảng giải 1 HS nhận xét câu a
HS trả lời miệng: Nối AI C/m Â1 = Â2
Một vài HS nhận xét
HS: cả lớp làm vào vở 1 HS nêu GT, KL bài toán HS:
để chứng minh ABC
cân ta chứng minh AB = AC, hoặc
HS phát hiện ABM và ACM có 2 cạnh và 1 góc bằng nhau, nhưng góc bằng nhau đó không xen giữa hai cạnh bằng nhau HS:
Từ M kẻ MK
HS: Một có 1 đường trung tuyến đồng thời là phân giác thì đó là cân
1HS đọc đề bài, 1 HS lên bảng vẽ hình và nêu GT, KL
HS quan sát hình vẽ trả lời
Một HS lên bảng chứng minh |
Năng lực tư duy, vận dụng.
Tư duy, giải quyết vấn đề.
Tư duy, làm chủ bản thân, hợp tác.
|
C. LUYỆN TẬP: Đã thực hiện ở trên
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG
Bài 1: Cho tam giác ABC có AB < AC. Tia phân giác củagóc A cắt đường phân giác của BC tại I. Kẻ IH vuông góc với đường thẳng AC. Chứng minh rằng BH = CK.
Bài 2: Đố. Em hãy thảo luận với các bạn và tìm hiểu trên Internet: Muốn đo khoảng cách giữa hai vật mà không thể đến trực tiếp được (Hai vật cần đo khoảng cách nằm ở hai địa điểm cách xa nhau) thì có thể dùng tính chất của hai tam giác bằng nhau và các dụng cụ đo trong kĩ thuật, trong xây dựng để đo được không?
Về nhà các em chuẩn bị bài tập trên để tiết sau chúng ta thực hành
E. HƯỚNG DẪN VỀ NHÀ (2’)
Về nhà làm tốt các bài tập 96; 97; 99; 100 tr 110 SBT
Hai tiết sau thực hành ngoài trời.
Mỗi tổ chuẩn bị: 4 cọc tiêu 1 giác kế 1 sợi dây dài khoảng 10m 1 thước đo.
Ôn lại cách sử dụng giác kế .
Tuần: 23 Tiết KHGD: 43+44 |
Ngày soạn: 27/01/2018 Ngày dạy: 29/01/2018 |
|
THỰC HÀNH NGOÀI TRỜI |
|
|
I. MỤC TIÊU:
1. Kiến thức: Biết cách xác định khoảng cách giữa hai địa điểm A và B trong đó có một địa điểm nhìn thấy nhưng không đến được. Biết dựng góc trên mặt đất, gióng đường thẳng. Chứng minh được những việc mình làm là đúng.
2. Kĩ năng: Rèn cho HS kỹ năng quan sát, phân tích, gióng 3 điểm thẳng hàng, đo độ dài đoạn thẳng.
3. Thái độ: Yêu thích bộ môn, nghiêm túc, phối hợp trong hoạt động tập thể.
4. Xác định nội dung trọng tâm của bài: Biết được cách xác định khoảng cách giữa hai địa điểm A và B trong thực tế. Có kĩ năng dựng góc trên mặt đất, gióng đường thẳng.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, hợp tác, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: SGK; SBT; Nghiên cứu tài liệu soạn bài, thước thẳng, com pa, thước đo góc. Chuẩn bị dụng cụ thực hành; Mẫu báo cáo cho 4 tổ.
BÁO CÁO THỰC HÀNH NGOÀI TRỜI
Của tổ ….., lớp…
KẾT QUẢ: AB = ………. ĐIỂM THỰC HÀNH CỦA TỔ
-
STT
Tên HS
Điểm chuẩn bị
dụng cụ
(3 điểm)
Ý thức
kỉ luật
(3 điểm)
Kĩ năng thực hành
(4điểm)
Tổng số điểm
(10 điểm)
Nhận xét chung (Tổ tự đánh giá) Tổ trưởng kí tên
2. Học sinh: Dụng cụ thực hành. SGK; SBT; Thước thẳng, com pa, thước đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
Thực hành ngoài trời về tam giác, tam giác bằng nhau |
Xác định được 2 điểm cần đo, biết sử dụng dụng cụ đo. |
Hiểu được các bước đo khoảng cách giữa 2 điểm mà 1 điểm không đến được |
Biết vận dụng giải bài toán thực tế đo khoảng cách trên mặt đất. |
Giải quyết các bài toán đo đạc và các bài toán thực tế. |
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: Lồng ghép trong thực hành
A. HOẠT ĐỘNG KHỞI ĐỘNG – HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 1. Thông báo nhiệm vụ và hướng dẫn cách làm (25’)
(1) Mục tiêu: Biết cách xác định khoảng cách giữa hai địa điểm A và B trong đó có một địa điểm nhìn thấy nhưng không đến được. Biết dựng góc trên mặt đất, gióng đường thẳng.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: HS biết cách đo khoảng cách giữa hai điểm A và B trong đó có một điểm nhìn thấy nhưng không đến được.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1. Nhiệm vụ: Cho trước hai cọc A và B, trong đó nhìn thấy cọc B nhưng không đi đến được B. Hãy xác định khoảng cách AB giữa hai chân cọc. * Hướng dẫn để đo đoạn thẳng AB (không trực tiếp đến được) ta làm như sau: - Bước 1: Đặt một cọc tiêu thẳng đứng tại vị trí A; dùng giác kế vạch đường thẳng xy vuông góc AB tại A. - Bước 2: Chọn một điểm E bất kì trên xy. Xác định điểm D sao cho E là trung điểm của AD. Đặt một cọn tiêu tại E. - Bước 3: Dùng giác kế vạch tia Dm vuông góc với xy. Bằng cách gióng thẳng hàng, chọn điểm C trên tia Dm sao cho các cọc tiêu cắm tại các vị trí B, E, C thẳng hàng. - Bước 4: Đo độ dài đoạn thẳng CD. -
Xét
AE = DE (gt)
Nên
Dựa vào độ dài đoạn CD. Từ đó đo được AB.
2. Chuẩn bị: Mỗi tổ HS chuẩn bị: - Bốn cọc tiêu, mỗi cọc dài khoảng 1,2 m. - Một giác kế. - Một sợi dây dài khoang 10m để kiểm tra kết quả. - Một thước đo.
|
- Đưa hình 149 lên bảng phụ và giới thiệu nhiệm vụ thực hành. - Gọi HS: Đọc lại nhiệm vụ trang 138 Sgk. - Vừa nêu các bước làm vừa vẽ dần để được hình 150 Sgk. Cho trước hai điểm A và B, giả sử hai điểm đó bị ngăn cách bởi con sông nhỏ, ta đang ở bờ sông có điểm A, nhìn thấy điểm B nhưng không tới được. Đặt giác kế tại điểm A vạch đường thẳng xy vuông góc với AB tại A. GV hỏi: Sử dụng giác kế thế nào để vạch được đường thẳng xy vuông góc với AB? GV
cùng 2 HS làm mẫu trước lớp cách vẽ đường thẳng
xy
Sau đó GV lấy 1 điểm E nằm trên đường thẳng xy. GV: Xác định điểm D sao cho E là trung điểm của AD. GV hỏi: Làm thế nào để xác định điểm D?
GV: Dùng giác kế đặt tại D vạch tia Dm vuông góc với AD. Cách làm như thế nào? GV: Dùng cọc tiêu, xác định trên tia Dm điểm C sao cho B, E, C thẳng hàng. GV: Đo độ dài đoạn CD. Vì sao khi làm như vậy ta lại có CD = AB?
Yêu cầu HS đọc lại phần hướng dẫn cách làm Sgk/138. GV: Yêu cầu các tổ báo cáo việc chuẩn bị thực hành của tổ về phân công nhiệm vụ và dụng cụ. GV: Kiểm tra cụ thể. Giao cho các tổ mẫu báo cáo thực hành. |
HS: Nghe và ghi bài
Đọc lại nhiệm vụ trang 138 Sgk.
HS trả lời:
2HS
làm mẫu trước lớp cách vẽ đường thẳng xy
HS lấy 1 điểm E nằm trên đường thẳng xy .
HS suy nghĩ cách xác định điểm D sao cho E là trung điểm của AD. HS: Có thể dùng dây đo đoạn thẳng AE rồi lấy trên tia đối của tia EA điểm D sao cho ED = EA. HS:
Cách làm tương tự như vạch đường thẳng xy
HS:
AE = DE (gt)
Nên
- Một HS đọc lại “Hướng dẫn cách làm” Sgk. HS: Các tổ trưởng báo cáo.
HS: Đại diện tổ nhận mẫu báo cáo.
|
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân.
|
Giải quyết vấn đề, giao tiếp, làm chủ bản thân.
|
B. HOẠT ĐỘNG LUYỆN TẬP
HOẠT ĐỘNG 2. Thực hành (60’)
(1) Mục tiêu: Học sinh đo được khoảng cách giữa hai điểm A, B trong thực tế như bài tập giáo viên đưa ra.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Kết quả đo khoảng cách giữa hai điểm A và B trong đó có một điểm nhìn thấy nhưng không đến được.
3. Thực hành:
Nội dung: Đo khoảng cách từ một cây xanh trong vườn trường đến một cây xanh ở sân trường.
|
GV bố trí cho hs tới địa điểm thực hành, phân công vị trí từng tổ. GV: Với mỗi cặp điểm A-B thì bố trí hai tổ cùng làm để đối chiếu kết quả, hai tổ lấy điểm E1, E2 nên lấy trên hai tia đối nhau gốc A để không vướng nhau khi thực hành. G
GV: Kiểm tra kĩ năng thực hành của các tổ, nhắc nhở, hướng dẫn thêm HS.
GV: Trong khi thực hành, mỗi tổ cần có thư kí ghi lại tình hình và kết quả thực hành. |
HS các tổ nghe GV bố trí tới địa điểm thực hành, phân công vị trí từng tổ.
HS xem: Sơ đồ bố trí hai tổ thực hành
HS: Các tổ thực hành như GV đã hướng dẫn, mỗi tổ có thể chia thành hai hoặc ba nhóm lần lượt thực hành để tất cả HS nắm được cách làm. HS: Tổ trưởng cử thư kí ghi lại tình hình và kết quả thực hành.
|
Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
|
C. HOẠT ĐỘNG VẬN DỤNG VÀ TÌM TÒI, MỞ RỘNG (3’)
1. Quan sát, tìm hiểu.
Quan sát xung quanh em và chỉ ra những công việc hay hình ảnh có liên quan đến đo khoảng cách giữa hai điểm trên mặt đất.
2. Thực hành đo khoảng cách trên mặt đất.
Hãy chọn một địa bàn khá phẳng (như sân trường, hay cánh đồng...) rồi chọn các mốc (Lá các cây to, hay cột điện hay đỉnh núi...) và tập đo khoảng cách hai vật trên mặt đất mà các em tự chọn, theo cách vừa học ở trên.
D. HƯỚNG DẪN VỀ NHÀ (2’)
- Làm bài tập thực hành, bài 102.SBT/110
- Làm câu hỏi 1, 2, 3 ôn tập chương II; bài tập 67, 68, 69 Sgk/140, 141
- Tiết sau ôn tập chương II.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
- Nêu các bước đo khoảng cách giữa hai địa điểm A và B trong đó có một địa điểm nhìn thấy nhưng không đến được. (MĐ2)
- Nêu các dụng cụ thực hành đo khoảng cách giữa hai địa điểm A và B trong đó có một địa điểm nhìn thấy nhưng không đến được. (MĐ1)
- Thực hành đo khoảng cách trên mặt đất. (MĐ3, 4)
Tuần: 23 Tiết KHGD: 44 |
Ngày soạn: 29/01/2018 Ngày dạy: 01/02/2018 |
|
ÔN TẬP CHƯƠNG II (tiết 1) |
|
|
I. MỤC TIÊU:
1. Kiến thức: Ôn tập, hệ thống lại các trường hợp bằng nhau của hai tam giác.
2. Kĩ năng: Vận dụng các kiến thức trường hợp bằng nhau của hai tam giác vào bài toán vẽ hình, tính toán, chứng minh.
3. Thái độ: Rèn tính cẩn thận, ý thức tự giác tư duy khoa học.
4. Xác định nội dung trọng tâm của bài: Ôn tập lại các trường hợp bằng nhau của hai tam giác. Vận dụng các kiến thức trường hợp bằng nhau của hai tam giác vào bài toán vẽ hình, tính toán, chứng minh.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ, bảng tổng kết các trường hợp bằng nhau của hai tam giác.
2. Học sinh: Trả lời câu hỏi ôn tập chương II, bảng nhóm, dụng cụ học tập.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Các trường hợp bằng nhau của tam giác.
|
Biết các trường hợp bằng nhau của tam giác.
|
|
Vận dụng chứng minh hai tam giác bằng nhau để giải các bài toán chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: Lồng ghép trong ôn tập
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Tiết học hôm nay, chúng ta sẽ ôn tập chương II về tam giác nhằm hệ thống kiến thức cơ bản của chương. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Hệ thống lại lí thuyết. (7’)
(1) Mục tiêu: Hệ thống được các kiến thức đã học trong chương tam giác.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Học sinh nắm được đầy đủ nội dung kiến thức chính của chương.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
I. Lý thuyết Bảng tổng kết chương II-Sgk
|
GV: Treo bảng phụ ghi bảng tổng kết chương II, chuyển giao nhiệm vụ: HS1: Viết công thức minh hoạ định lý tổng ba góc của tam giác và tính chất của góc ngoài của tam giác vào hình vẽ tương ứng, rồi phát biểu các tính chất đó. HS2: Dùng kí hiệu để biểu diễn định nghĩa, tính chất về góc, cạnh của tam giác cân, tam giác đều, điền vào bảng, rồi phát biểu định nghĩa, tính chất đó và nêu các dấu hiệu nhận biết. |
HS: Dùng kí hiệu biểu diễn định nghĩa, tính chất về góc cạnh của tam giác vuông, tam giác vuông cân ghi vào bảng, rồi phát biểu định nghĩa, tính chất đó. Nêu dấu hiệu nhận biết, ...
|
Giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân.
|
HOẠT ĐỘNG 3. Luyện tập. (35’)
(1) Mục tiêu: HS vận dụng kiến thức đã học để giải một số dạng toán cơ bản.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: HS có kĩ năng vẽ hình, kĩ năng chứng minh, kĩ năng suy luận và phát triển bài toán hình học.
II. Luyện tập 1. Bài 1 (Bài 68.Sgk/141) a, b)Suy từ định lý tổng ba góc trong tam giác c) t/c về góc của tam giác cân d) từ định lý : Nếu một tam giác có hai góc bằng nhau thì tam giác là tam giác cân 2. Bài 2 (Bài 67.Sgk/140) 1) Đ; 2) Đ 3) S ; 4) S 5) Đ; 6) S
3
GT
A
AB
= AC
BD
= CD
KL
Chứng minh
Xeùt
AB = AC (gt) DB = DC (gt)
AD
là cạnh chung
Nên
Xét
AB = AC (gt)
AI cạnh chung
Nên
mà
4
Chứng minh Xét
OA = OC (gt)
OD = OB (vì OA = OC và AB = CD) Do
đó
mà
Do
đó: Xét
AB=CD(gt)
Xét
O OK cạnh chung AK = CK (cmt) (c.c.c)
|
GV: Treo bảng phụ ghi bài 68.SGK/141. Cho HS đứng tại chỗ trả lời
GV: Treo bảng phụ ghi bài 67 Sgk/140 Gọi 3 Hs lên bảng
GV: Treo bảng phụ ghi bài 69.Sgk/141 GV: Vẽ hình lên bảng H: Hãy cho biết GT& KL của bài toán. GV: Gợi ý HS phân tích
Cần
thêm
GV gọi HS lên bảng trình bày
H: Qua bài tập này ta rút ra cách vẽ đường thẳng đi qua điểm A và vuông góc với đường thẳng a bằng compa và thước như thế nào?
GV: Treo bảng phụ ghi đề bài 108 SBT/111 H: Hãy cho biết GT&KL của bài toán? GV cho HS h.động nhóm GV: Gợi ý phân tích bài OK
là tia phân giác của
Cần thêm KA = KC
Thêm
GV gọi đại diện 1 nhóm lên bảng trình bày
GV: Sửa bài sai GV: Qua bài này ta có thể vẽ tia phân giác của một góc bằng thước mà không cần compa và thước đo góc. |
HS đứng tại chỗ trả lời
3 HS lần lượt lên đánh dấu 1) Đ ; 2) Đ 3) S ; 4) S 5) Đ ; 6) S HS đọc đề bài 69 Sgk/141 HS: Vẽ hình vào vở HS: Ghi GT& KL của bài toán HS: Lần lượt trả lời các câu hỏi gợi ý của GV.
HS lên bảng trình bày
HS: Qua A vẽ một cung cắt a tại B và C - Vẽ 2 cung tâm B và C cùng bán kính cắt nhau tại một điểm khác A - Đường thẳng AD vuông góc a 1HS: Đọc to đề đề bài 108 HS: Cho biết GT&KL của bài toán. HS: Hoạt động nhóm
HS nghe GV: Gợi ý phân tích bài
HS: Nhận xét - Sửa bài sai
|
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, hợp tác, làm chủ bản thân.
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, hợp tác, làm chủ bản thân.
|
C. LUYỆN TẬP: Đã thực hiện ở trên
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG (1’)
H: Em hãy thảo luận với các bạn và tìm hiểu trên Internet: Hình ảnh tam giác còn được vận dụng trang trí trong thời trang, trong kiến trúc và trong đời sống?
E. HƯỚNG DẪN VỀ NHÀ (1’)
- Ôn tập các trường hợp bằng nhau tam giác.
- Xem lại các bài tập đã làm
- Ôn tập tiếp định lý tổng 3 góc của tam giác và hệ quả, các tam giác đặc biệt.
- Làm bài tập 70, 71, 72, 73.Sgk/141
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Nhắc lại các trường hợp bằng nhau của 2 tam giác? (MĐ1)
Câu 2: Làm bài tập trong hoạt động 3. (MĐ3)
DUYỆT CỦA CHUYÊN MÔN DUYỆT CỦA TỔ
Chư Prông, ngày.......tháng.......năm 2018 Chư Prông, ngày.......tháng.......năm 2018
Tuần: 24 Tiết KHGD: 46 |
Ngày soạn: 04/02/2018 Ngày dạy: 06/02/2018 |
|
ÔN TẬP CHƯƠNG II (tt) |
|
|
I. MỤC TIÊU:
1. Kiến thức: Tiếp tục hệ thống kiến thức đã học trong chương tam giác; Giải một số dạng toán cơ bản liên quan đến kiến thức trong chương này; Vận dụng kiến thức để chứng minh 2 tam giác bằng nhau, hai đoạn thẳng bằng nhau, hai góc bằng nhau, tam giác cân, đều, vuông.
2. Kĩ năng: Tính số đo góc, số đo cạnh; Sử dụng thành thạo các công cụ đo góc, đo đoạn thẳng; Hình thành kỹ năng giải quyết các bài toán, chứng minh các bài toán có nội dung thực tế.
3. Thái độ: Tính nghiêm túc, tích cực, chủ động, độc lập và hợp tác trong hoạt động nhóm.
Sự say xưa, hứng thú trong học tập và tìm tòi nghiên cứu liên hệ thực tiễn
4. Xác định nội dung trọng tâm của bài: Ôn tập lại kiến thức đã học về tam giác cân, tam giác đều, tam giác vuông, tam giác vuông cân. Vận dụng các kiến thức của hai tam giác đặc biệt vào bài toán vẽ hình, tính toán, chứng minh.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, gqvđ, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, compa, êke, thước đo độ, bảng phụ Bảng ôn tập một số dạng đặc biệt.
2. Học sinh: Thực hiện hướng dẫn tiết trước Thước thẳng, êke, compa.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Tam giác.
|
Học sinh thuộc các định nghĩa, định lí chương II.
|
|
Vận dụng các kiến thức trong chương để chứng minh hai tam giác bằng nhau, hai đoạn thẳng bằng nhau.
|
Vận dụng các kiến thức trong chương để phát triển bài toán tùy theo năng lực của mỗi Hs Ứng dụng các kiến thức của chương vào thực tế. |
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: Lồng ghép trong ôn tập
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Tiết học hôm nay, chúng ta sẽ tiếp tục ôn tập chương II về tam giác nhằm hệ thống kiến thức cơ bản của chương. |
HS lắng nghe |
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Luyện tập. (36’)
(1) Mục tiêu: HS vận dụng kiến thức đã học để giải một số dạng toán cơ bản. HS có kĩ năng vẽ hình, kĩ năng chứng minh và kĩ năng suy luận và phát triển bài toán hình học. Hs biết cách chứng minh tam giác vuông theo định lí Pitgo đảo. Chứng minh thành thạo hai tam giác vuông bằng nhau.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải đầy đủ nội dung các bài toán.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1. Bài tập 105.SBT/111Chứng minhXét AEC; Ê = 1v có: EC2 = AC2 AE2 (pytago) EC2 = 52 42 EC = 3; BE = BC EC = 9 3 = 6 Xét ABE, Ê = 1v có: AB2 = AE2 + BE2 (pytago) = 42 + 62 = 52 AB
=
ABC có: AB2 + AC2 = 52 + 25 = 77 BC2 = 92 = 81 AB2 + AC2 BC2 Nên ABC không là vuông 2. Bài tập 70. Sgk/141
Chứng minha) ABC cân (gt)
Xét ABM và CAN, có: AB
= AC (gt), Nên ABM = CAN (c.g.c) Do đó AMN cân b)
Xét
ABH
và ACK
( HÂB = KÂC (vì ABM = CAN). Do đó ABH = ACK (c.h-g.n) BH = CK (2 cạnh t/ứng) c) Vì ABH = ACK (câu b) AH = AK (hai cạnh t/ứng) d)
Xét MHB
và NKC
( MB
= NC(gt);
NênMHB = NKC (c.h-g.n)
mà
OBC cân tại O e)
Khi BÂC = 600
ABC
là
đều
Có
ABM
cân (vì BA = BM =BC)
HMB
có
OBC
cân (cmt) có
OBC là đều. |
GV: Sử dụng bài tập 105 SBT trên bảng phụ
GV gọi 1HS: ABC có phải là tam giác vuông không ?
GV: Cách giải bài 73 tương tự như bài 105 vừa giải. Các em về nhà làm; GV treo bảng phụ bài 70.Sgk/141 GV gọi 1HS lên bảng vẽ hình (đến câu d) GV gọi HS nêu GT, KL bài toán
GV lần lượt gọi HS làm miệng câu: a) C/m: AMN cân HS: trình bày miệng xong. GV đưa bài C/m viết sẵn để HS ghi nhớ
GV lần lượt gọi 3 HS lên bảng làm các câu b, c, d
GV gọi H S nhận xét và b sung chỗ sai sót
GV đưa hình vẽ của câu e) lên bảng phụ: H: khi BÂC = 600 và BM = CN = BC thì suy ra được điều gì ? H: OBC khi đó là gì? GV gọi 1 HS lên bảng trình bày GV gọi HS nhận xét |
HS: đọc đề bài bảng phụ và quan sát hình vẽ; Một HS lên bảng tính AB HS tính và sau đó đưa ra kết luận ABC không phải là vuông
HS: về nhà giải.
1HS đọc đề bài 1 HS lên bảng vẽ hình (đến câu d)
HS nêu GT, KL bài toán
1HS làm miệng câu a
HS: cả lớp chép bài (câu a) và ghi nhớ
3HS lần lượt lên bảng
HS1: câu b HS2: câu c HS3: câu d
Một vài HS nhận xét bài làm của bạn
HS: Quan sát hình vẽ câu (e) và suy nghĩ. HS:
suy ra
HS: OBC là đều;
1HS lên bảng trình bày; Một vài HS nhận xét ; |
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, hợp tác, làm chủ bản thân.
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, hợp tác, làm chủ bản thân
|
C. LUYỆN TẬP: Đã thực hiện ở trên
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG
HOẠT ĐỘNG 2. Vận dụng, tìm tòi. (7’)
(1) Mục tiêu: Tạo cho hs nhu cầu tìm hiểu ứng dụng của tam giác trong đời sống và trong khoa học. Hình thành năng lực ứng dụng CNTT, tự nghiên cứu, quan sát, tổng hợp, …
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Kết quả tìm hiểu của các nhóm về ứng dụng của hình ảnh tam giác trong thời trang, kiến trúc, các lĩnh vực khác trong đời sống. Tìm hiểu được tam giác vàng là gì? Tỉ lệ vàng là gì? Có bao nhiêu tam giác vàng trong hình. Chỉ ra tam giác đặc biệt. Ứng dụng của tam giác vuông có độ dài các cạnh 3; 4; 5 trong các lĩnh vực khác.
Bài tập: Ngũ giác, hình sao năm cánh và tam giác vàng: + Từ một ngũ giác đều có thể tạo ra hình sao năm cánh bằng cách nối các đường chéo của ngũ giác với nhau. Trong hình sao năm cánh có xuất hiện những tam giác vàng. + Tam giác vàng là tam giác cân có góc ở đỉnh bằng 36o và hai góc ở đáy bằng 72o. Tỉ lệ giữa cạnh bên và cạnh đáy của nó là tỉ lệ vàng. Khi kẻ đường phân giác của góc ở đáy thì đường phân giác sẽ chia cạnh đối diện theo tỉ lệ vàng và tạo ra thêm hai tam giác cân nhỏ hơn, trong đó có một tam giác vàng. (Trích trong "Niềm vui Toán học" - Theoni Pappas - NXB Dân Trí 2014)
|
+ Gv phát phiếu tập cho học sinh có nôi dung như trên. + Yêu cầu học sinh về nhà làm việc theo nhóm để thảo luận, cùng nhau tìm hiểu trên mạng Internet về ứng dụng của hình ảnh tam giác trong thời trang, kiến trúc, các lĩnh vực khác trong đời sống. Sau khi tìm hiểu các em có thể in ra hoặc chụp ảnh hoặc quay video. + Ngũ giác, hình sao năm cánh và tam giác vàng: Từ một ngũ giác đều có thể tạo ra hình sao năm cánh bằng cách nối các đường chéo của ngũ giác với nhau. Trong hình sao năm cánh có xuất hiện những tam giác vàng. Em tìm hiểu thế nào là tam giác vàng, tỉ lệ vàng là gì? Có bao nhiêu tam giác vàng? + Các em hoàn thành nội dung trong phiếu học tập sau 1 tuần. |
Hs ở nhà làm việc theo nhóm để hoàn thành nội dung phiếu học tập.
|
Giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân.
|
E. HƯỚNG DẪN VỀ NHÀ (1’)
- Ôn tập lý thuyết và làm các bài tập chương II.
- Tiết sau kiểm tra 1 tiết.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: GV yêu cầu HS nhắc lại các đặc biệt. (MĐ1)
Câu 2: Các bài tập củng cố thể hiện trong mục B "Hoạt động luyện tập". (MĐ3)
Câu 3: Bài tập củng cố thể hiện trong mục D "Hoạt động vận dụng, tìm tòi". (MĐ4)
Tuần: 24 Tiết KHGD: 47 |
Ngày soạn: 01/02/2018 Ngày dạy: 09/02/2018 |
KIỂM TRA CHƯƠNG II
I. MỤC TIÊU
1. Kiến thức: Nhằm đánh giá khả năng vận dụng các trường hợp bằng nhau của tam giác vào việc giải toán. Chứng minh sự bằng nhau về góc, về đoạn thẳng; Nắm được nội dung định lý Pytago và biết vận dụng vào tính toán.
2. Kỹ năng: Kiểm tra kĩ năng vẽ hình, sử dụng đúng tên gọi các tam giác, các góc, các cạnh có trong hình vẽ. Kĩ năng trình bày bài toán hình cơ bản.
3. Thái độ: Tính nghiêm túc, khả năng suy nghĩ độc lập, sáng tạo khi làm bài.
4. Xác định nội dung trọng tâm của bài: Nắm vững kiến thức chương II.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, làm chủ bản thân.
- Năng lực chuyên biệt: Xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Ra đề, đáp án, thang điểm.
2. Học sinh: Ôn tập các kiến thức chương II.
III. MA TRẬN ĐỀ:
Mức độ
Chủ đề |
Nhận biết |
Thông hiểu |
Vận dụng |
Cộng |
|
Cấp độ thấp |
Cấp độ cao |
||||
1. Tổng ba góc trong tam giác |
Tính được số đo của 1 góc trong tam giác |
|
|
|
|
Số câu Số điểm Tỉ lệ % |
1 1,5
|
|
|
|
1 1,5 15% |
2. Các trường hợp bằng nhau của hai tam giác |
Biết chứng minh hai tam giác bằng nhau |
Vẽ hình, viết GT, KL. Từ hai tam giác bằng nhau rồi suy ra hai đoạn thẳng hoặc hai góc bằng nhau |
|
|
|
Số câu Số điểm Tỉ lệ % |
1 1,0
|
2 2,0
|
|
|
2 3,0 30% |
3. Tam giác cân |
|
|
Chứng minh tam giác cân |
Biết áp dụng để c/m tam giác đều |
|
Số câu Số điểm Tỉ lệ % |
|
|
1 1,0
|
1 1,0
|
2 2,0 20% |
4. Định lý Py-ta-go |
Sử dụng định lý Py ta go tính độ dài các cạnh |
Sử dụng định lý Py ta go tính độ dài các cạnh |
Sử dụng định lí Pytago đảo để chứng minh tam giác vuông |
|
|
Số câu Số điểm Tỉ lệ % |
1 1,25
|
1 1,25
|
1 1,0
|
|
3 3,5 35% |
Tổng số câu Tổng số điểm Tỉ lệ % |
3 3,75 37,5% |
2 3,25 32,5% |
3 3,0 30% |
8 10,0 100% |
|
IV. ĐỀ BÀI
Bài 1: (1,5 điểm)
Cho
tam giác DEK biết
![]() ,
,
![]() .Tính
số đo góc D?
.Tính
số đo góc D?
B ài
2:
(3,5 điểm)
ài
2:
(3,5 điểm)
Trên hình vẽ bên: Cho tam giác ABC có AH vuông góc BC,
biết AH = 12 cm, BH = 9 cm, AC = 20 cm.
Tính độ dài các đoạn thẳng AB, HC ?
Tam giác ABC là tam giác gì? Vì sao?
Bài 3: (5,0 điểm)
Cho
tam giác ABC vuông tại A có góc C = 300.
Tia phân giác của góc B cắt AC tại E. Kẻ EK vuông góc
với BC ( K
![]() BC )
BC )
a)
Chứng minh
![]() ABE =
ABE =
![]() KBE.
KBE.
b) Chứng minh EB là tia phân giác của góc AEK.
c)
Chứng minh
![]() BEC
cân.
BEC
cân.
d) Kẻ CH vuông góc với đường thẳng BE tại H. Chứng minh KH = KC.
V. HƯỚNG DẪN HỌC Ở NHÀ
- Kiểm tra lại bài làm qua vở ghi.
- Xem trước bài ”Tổng ba góc của một tam giác”.
ĐÁP ÁN, BIỂU ĐIỂM KIỂM
Bài |
Câu |
Đáp án |
Điểm |
Bài 1 (1,5 điểm)
|
|
Xét
|
0,5
0,25 0,25 0,25 0,25 |
Bài 2 (3,5 điểm) |
a) |
Áp
dụng định lí Pitago vào
AB2 = AH2 + BH2
Áp
dụng định lí Pitago vào
AC2 = AH2 + CH2
|
0,5
0,75
0,5
0,75 |
b) |
Ta có BC = BH + CH = 9 + 16 =25 AB2 = 152 = 225 AC2 = 202 = 400 BC2 = 252 = 625 Vì BC2 = AB2 + AC2 (= 625) Nên
|
0,5
0,5 |
|
Bài 3 (5,0 điểm)
|
|
Hình vẽ câu a và ghi giả thiết, kết luận đúng
|
1,0 |
a) |
Xét hai tam giác vuông ABE và KBE, có: BE là cạnh chung
Nên |
0,25 0,25 0,25 0,25 |
|
b) |
Vì
|
0,25 0,25 0,5 |
|
c) |
Vì
Vì
BE là phân giác của góc B Xét
|
0,25
0,25
0,5 |
|
d) |
Ta
có
Mà
Xét 2 tam giác vuông EKC và EHC, có: EC
cạnh chung;
Do
đó
Mà
|
0,5 0,5 |
* Lưu ý: Học sinh giải cách khác đúng vẫn cho điểm tối đa.
I V.
ĐỀ
BÀI
V.
ĐỀ
BÀI
Bài 1: (1,5 điểm)
Phát biểu định lý tổng ba góc của một tam giác?
Áp dụng: Tìm số đo x trên hình vẽ bên?
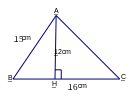
Bài 2: (3,5 điểm)
Cho
![]() ABC
như hình vẽ bên, có:
ABC
như hình vẽ bên, có:
AB = 15cm, AH = 12cm và HC = 16cm.
a) Tính các độ dài AC, BH.
b)
Chứng minh
![]() ABC
là tam giác vuông.
ABC
là tam giác vuông.
Bài 3: (5,0 điểm)
Cho
tam giác ABC vuông tại A có góc C = 300.
Tia phân giác của góc B cắt AC tại E. Kẻ EK vuông góc
với BC (K
![]() BC)
BC)
a)
Chứng minh
![]() ABE
=
ABE
=
![]() KBE.
KBE.
b) Chứng minh EB là tia phân giác của góc AEK.
c)
Chứng minh
![]() BEC
cân.
BEC
cân.
d)
Kẻ CH vuông góc với đường thẳng BE tại H. Chứng minh
![]() HCK
là tam giác đều.
HCK
là tam giác đều.
V. HƯỚNG DẪN HỌC Ở NHÀ
- Kiểm tra lại bài làm qua vở ghi.
- Xem trước bài ”Tổng ba góc của một tam giác”.
ĐÁP ÁN, BIỂU ĐIỂM KIỂM
Bài |
Câu |
Đáp án |
Điểm |
Bài 1 (1,5 điểm)
|
a) |
Phát biểu đúng định lý tổng ba góc của một tam giác |
1,0 |
b) |
Áp dụng định lí tổng ba góc trong tam giác, ta có:
|
0,5 |
|
Bài 2 (3,5 điểm) |
a) |
AC2 = HA2 + HC2 = 122 + 162 = 400
BH2 = BA2 – HA2 = 152 – 122 = 81
|
0,75 0,5
0,75 0,5 |
b) |
Ta có: BC = BH + CH = 9 + 16 = 25 BC2 = 252 = 625 AB2 + AC2 = 152 + 202 = 625
Nên
|
0,25
0,25 0,25 0,25 |
|
Bài 3 (5,0 điểm)
|
|
Hình vẽ câu a và ghi giả thiết, kết luận đúng
|
1,0 |
a) |
Xét hai tam giác vuông ABE và KBE, có: BE là cạnh chung
Nên |
0,25 0,25 0,25 0,25 |
|
b) |
Vì
|
0,25 0,25 0,5 |
|
c) |
Vì
Vì BE là phân giác của góc B
Xét
|
0,25
0,25
0,5 |
|
d) |
Ta
có
Mà
Xét 2 tam giác vuông EKC và EHC, có: EC cạnh chung
Do
đó
Nên tam giác HCK cân Mà
|
0,5
0,5 |
* Lưu ý: Học sinh giải cách khác đúng vẫn cho điểm tối đa.
Tuần: 25 Tiết KHGD: 48 |
Ngày soạn: 24/02/2018 Ngày dạy: 26/02/2018 |
|
§1. QUAN HỆ GIỮA GÓC VÀ CẠNH ĐỐI DIỆN TRONG MỘT TAM GIÁC |
|
|
I. MỤC TIÊU:
1. Kiến thức: Học sinh biết quan hệ giữa góc và cạnh đối diện trong một tam giác. Học sinh nắm vững được nội dung hai định lý.
2. Kĩ năng: Biết vẽ hình đúng yêu cầu và dự đoán, nhận xét các tính chất qua hình vẽ. Biết vận dụng các mối quan hệ giữa góc và cạnh đối diện trong một tam giác để ứng dụng vào bài cụ thể. Biết tóm tắt định lý; tóm tắt GT, KL bài toán.
3. Thái độ: Giáo dục tính chính xác, óc tư duy sáng tạo.
4. Nội dung trọng tâm: Biết được quan hệ giữa góc và cạnh trong tam giác.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, gqvđ, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước kẻ, compa, thước đo góc. Tam giác ABC bằng giấy có AB < AC.
2. Học sinh: Thước kẻ, compa, thước đo độ. Tam giác ABC bằng giấy có AB < AC. Ôn lại kiến thức cũ về tính chất góc ngoài của tam giác, tổng ba góc trong tam giác.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Góc đối diện với cạnh lớn hơn |
Biết nhận ra góc đối diện với cạnh lớn hơn |
|
|
|
2. Cạnh đối diện với góc lớn hơn |
|
|
Tìm ra cạnh đối diện với góc lớn hơn |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: Trả bài kiểm tra (3’)
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (5’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Trong chương II, các em đã được tìm hiểu một số nội dung về quan hệ giữa các góc trong tam giác, về hai tam giác bằng nhau, ... Tiếp tục chuỗi kiến thức với tam giác, ta sẽ tìm hiểu về: Quan hệ giữa các yếu tố cạnh, góc trong một tam giác. Các đường đồng quy của tam giác. GV:
Vẽ
|
HS lắng nghe
HS: góc C đối diện với cạnh AB HS:
HS:
|
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Tìm hiểu quan hệ giữa góc và cạnh đối diện (16’)
(1) Mục tiêu: HS nhận biết được mối quan hệ giữa góc và cạnh đối diện trong tam giác.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài toán và nội dung định lý 1.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1. Góc đối diện với cạnh lớn hơn.
* Định lí 1: Sgk/54
G
Kl
Chứng minh: Trên tia AC lấy B’: AB’= AB. Kẻ tia phân giác AM của góc A (M BC) Xét ABM và AB’M, có: AB = AB’ (do cách lấy B’)
AM cạnh chung ABM = AB’M (c.g.c)
Góc AB’M là góc ngoài của B’MC Nên
ta có
Từ
(1) và (2) suy ra
|
GV:
Vẽ
b)
GV: Hướng dẫn HS gấp hình theo ?2 sgk . -
Hãy so sánh
-
Vì sao
-
-
Vậy ta có nhận xét gì về quan hệ giữa
GV: Hãy rút ra kết luận về quan hệ giữa góc và cạnh đối diện trong một tam giác? GV: Giới thiệu định lí 1 sgk. GV: Hãy viết tóm tắt định lí dưới dạng gt, kl ? H:
Làm như thế nào để có thể chứng minh được
GV: Hướng dẫn cách lấy điểm B’ và kẻ phân giác AM của góc A. GV: Nhận xét gì về ABM và AB’M? Từ ABM = AB’M ta suy ra được điều gì? GV: Góc AB’M là góc ngoài của B’MC. Theo tính chất ta có điều gì? GV:
Trong
|
HS theo dõi trên bảng HS dưới lớp làm quan sát và đưa ra dự đoán
HS lấy tam giác đã cắt trước ở nhà ra gấp.
HS: Lần lượt trả lời các câu hỏi.
HS: Kết luận. 2 học sinh nhắc lại định lý 1 1HS lên bảng viết giả thiết kết luận . HS: Kẻ thêm tia phân giác của góc A
1HS lên bảng giải.
|
Năng lực tự học và tính toán.
Năng lực sử dụng ngôn ngữ toán học, sử dụng các công thức tổng quát |
HOẠT ĐỘNG 3. Tìm hiểu quan hệ giữa cạnh đối diện với góc lớn hơn (14’)
(1) Mục tiêu: Học sinh nhận biết được mối quan hệ giữa cạnh và góc đối diện trong tam giác
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải bài toán và nội dung định lý 2.
2) Cạnh đối diện với góc lớn hơn: ?3:
AC > AB. * Định lý 2: Sgk/55. * Nhận xét: |
HS: Làm ?3. GV: Tại sao có thể kết luận được AC > AB ?
GV: Từ định lý 1 và 2 em có nhận xét gì? GV: Trong tam giác vuông cạnh nào lớn nhất? GV: Đó là nội dung của nhận xét. |
HS:
Nếu AC = AB thì
HS: Trả lời
1HS đọc to nhận xét.
|
Năng lực sử dụng ngôn ngữ toán học, sử dụng các công thức tổng quát |
C. LUYỆN TẬP, VẬN DỤNG
HOẠT ĐỘNG 4. Củng cố (6’)
(1) Mục tiêu: Củng cố cho HS kiến thức về mối quan hệ giữa góc và cạnh đối diện trong tam giác.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài tập 1, 2.
Chuyển giao: Yêu cầu HS làm bài tập: Bài 1: Cho tam giác MNP có MN = 8cm; MP = 10cm; NP = 12cm. Hãy so sánh các góc của tam giác MNP H: Chỉ với thước thẳng ta có thể so sánh được các góc của một tam giác hay không? Làm bằng cách nào?
Bài
2: Cho
∆XYZ biết
H: Chỉ với thước đo góc ta có thể so sánh được các cạnh của một tam giác hay không? Làm bằng cách nào?
|
HS: hoạt động theo nhóm làm bài + ∆MNP, có MN = 8cm; MP = 10cm; NP = 12cm MN < MP < NP
+
∆XYZ,
biết:
YZ < XZ < XY HS thảo luận nhóm đôi |
Năng lực giao tiếp, hợp tác, làm chủ bản thân |
D. HƯỚNG DẪN VỀ NHÀ (1’)
- Học bài theo vở ghi và Sgk.
- Làm bài tập 1; 2 Sgk/55.
- Chuẩn bị bài tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Các bài tập củng cố thể hiện trong "Hoạt động luyện tập, vận dụng" (MĐ 1, 3).
Tuần: 25 Tiết KHGD: 49 |
Ngày soạn: 24/02/2018 Ngày dạy: 28/02/2018 |
LUYỆN TẬP
I. MỤC TIÊU
1. Kiến thức: Củng cố các định lý quan hệ giữa góc và cạnh đối diện trong một tam giác.
2. Kỹ năng: Rèn luyện kỹ năng vận dụng các định lý đó để so sánh các đoạn thẳng, các góc trong tam giác.
3. Thái độ: Giáo dục tính cẩn thận, cần cù, chính xác, tư duy sáng tạo, bước đầu biết phân tích để tìm hướng c/m, trình bày bài, suy luận có căn cứ.
4. Nội dung trọng tâm của bài: Biết quan hệ giữa góc và cạnh đối diện trong một tam giác. Nắm vững được nội dung hai định lý. Biết tóm tắt định lý; ghi GT, KL của b/toán.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ ghi câu hỏi , bài tập, thước, compa, thước đo góc.
2. Học sinh: Bảng nhóm, thước thẳng, compa, thước đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Quan hệ giữa góc và cạnh đối diện trong một tam giác. |
Biết quan hệ giữa góc và cạnh đối diện trong một tam giác. |
|
Biết vận dụng các mối quan hệ giữa góc và cạnh đối diện trong một tam giác để ứng dụng vào bài cụ thể. Biết tóm tắt định lý; GT, KL bài toán. Tìm ra cạnh đối diện với góc lớn hơn |
Sử dụng định lý trong các bài toán thực tế. |
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5')
H: Phát biểu định lí về quan hệ giữa góc và cạnh đối diện trong một tam giác?
Làm bài tập: a) So sánh các cạnh của tam giác ABC, biết: AB = 3cm, BC = 6cm, AC = 5cm.
b)
So sánh các góc của tam giác ABC, biết: Â
= 800,![]() ,
,
![]() .
.
Đáp án: Trong một tam giác cạnh đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại. 4đ
a)
Ta
có BC
> AC > AB (vì 6 > 5 > 3) nên
![]() >
>
![]() >
>
![]() (Đlí liên hệ giữa cạnh và góc...) ...3đ
(Đlí liên hệ giữa cạnh và góc...) ...3đ
b)
Tương tự:
![]() <
<
![]() < Â => AC < AB < BC (Đlí
liên hệ giữa cạnh và góc...) ...3đ
< Â => AC < AB < BC (Đlí
liên hệ giữa cạnh và góc...) ...3đ
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Ở tiết học trước các em đã được biết quan hệ giữa góc và cạnh đối diện trong một tam giác. Tiết học hôm nay các em sẽ được củng cố các định lý về quan hệ giữa góc và cạnh đối diện trong một tam giác. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Luyện tập (31’)
(1) Mục tiêu: Biết vận dụng các mối quan hệ giữa góc và cạnh đối diện trong một tam giác để ứng dụng vào bài cụ thể.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài toán.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1
a)Trong
Vậy
b)
Ta có
2
Giải -
Xét DBC,
có:
DB
> DC (1) ( Q.hệ giữa góc và cạnh đối diện trong
tam giác. Có
-
Xét DAB,
có:
DA > DB (2) Từ (1) và (2) suy ra: DA > DB > DC. Vậy Hạnh đi xa nhất, Trang đi gần nhất.
3
G Kl
So
sánh
Giải: Lấy D thuộc tia AM sao cho MD = MA. Xét AMB và DMC, có: MB = MC (gt)
MA = MD (cách vẽ) Nên AMB = DMC (c.g.c)
và AB = DC (2 cạnh t.ứng) Xét ADC, có AC > AB(gt) AB = DC (c/m trên)
AC
> DC
Mà
Hay
|
Gv: Yêu cầu Hs sửa bài 3.Sgk Giáo viên hướng dẫn lại. H:
Từ đó đi đến kết luận gì? Vậy cạnh lớn nhất trong tam giác đó là cạnh nào? H: Tam giác ABC là tam giác cân vì sao? H: Vậy trong tam giác tù thì cạnh nào lớn nhất?Vì sao? GV: Đưa đề bài và h.vẽ bài 5 lên bảng phụ. H: Để so sánh 3 đoạn thẳng DA; DB; DC ta dựa vào những nào? H: Tại sao góc C lớn hơn góc B1? Từ đó ta có kết luận gì về hai đoạn DB và DC ? H: Tương tự như vậy, háy so sánh góc B2 với góc A, ta có kết luận gì? H: Hãy cho biết trong ba đoạn DA; DB; DC đoạn nào dài nhất, đoạn nào ngắn nhất? vì sao? H: Từ đó ai đi xa nhất, ai đi gần nhất? H: Áp dụng kiến thức nào để làm như vậy? GV: Treo bảng phụ ghi bài 7 SBT/24, yêu cầu HS đọc bài GV: Bài toán cho ta biết gì? Yêu cầu chứng minh điều gì? lên bảng vẽ hình và ghi gt, kl của b.toán? H:
Để so sánh
GV gợi ý: Trên tia đối của tia MA lấy điểm D sao cho MD = MA H:
Theo em
H:
Vậy để so sánh
GV: Muốn vậy ta xét ADC, yêu cầu thực hiện trên bảng
GV gọi HS khác nhận xét |
HS: Lên sửa bài về nhà.
Học sinh nhận xét.
HS: Trả lời
HS: Đọc đề bài 5 Sgk HS: Hoạt động theo nhóm để tìm xem ai đi xa nhất và giải thích.
HS: Trả lời
HS: Làm nhóm.
HS: Kết luận
HS: Trả lời
HS: Đọc đề, vẽ hình, ghi GT & KL
HS:
HS:
Để so sánh
HS: Thực hiện trên bảng.
HS khác nhận xét
|
Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, tính toán, hợp tác, làm chủ bản thân.
|
C. LUYỆN TẬP: Đã thực hiện ở mục B
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG
HOẠT ĐỘNG 3. Vận dụng, tìm tòi (7’)
(1) Mục tiêu: Vận dụng kiến thức đã học vào thực tế.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp, thực hành, trực quan/ kỹ thuật động não.
(3) Hình thức tổ chức hoạt động: Hoạt động nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Bài làm của học sinh.
+ Chuyển giao:
- Đưa ra bức tranh yêu cầu HS tìm các cách để trả lời câu hỏi
Người nào bơi quãng đường ngắn nhất?
Các em hãy dự đoán xem, đường đi của bạn nào ngắn hơn?
+ Thực hiện:
- GV Chia lớp thành các nhóm thảo luận trả lời
- HS quan sát bức tranh thảo luận nhóm dự kiến các tình huống đặt ra để trả lời câu hỏi.
- GV quan sát hoạt động của các nhóm hỗ trợ HS trong quá trình thảo luận.
+ Báo cáo, thảo luận:
- Đại diện nhóm báo cáo kết quả thảo luận của nhóm mình.
- Các nhóm khác theo dõi lắng nghe, nêu ý kiến
- Đại diện nhóm giải trình các thắc mắc của nhóm khác (Nếu có)
+ Đánh giá, nhận xét, tổng hợp
- GV đánh giá kết quả thảo luận của học sinh, tinh thần hợp tác. GV gợi mở để HS tìm hiểu kiến thức mới.
E. HƯỚNG DẪN VỀ NHÀ (1’)
- Học thuộc 2 định lý quan hệ giữa góc và cạnh đối diện trong tam giác
- Làm bài tập 5, 6, 8 (SBT/24, 25)
- Ôn lại định lý Pitago.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
GV: Củng cố bài lồng ghép vào quá trình luyện tập.
Các bài tập củng cố thể hiện trong "Hoạt động 2, 3". (MĐ1, 3, 4)
DUYỆT CỦA CHUYÊN MÔN DUYỆT CỦA TỔ
Chư Prông, ngày.......tháng.......năm 2018 Chư Prông, ngày.......tháng.......năm 2018
Tuần: 26 Tiết KHGD: 50 |
Ngày soạn: 03/03/2018 Ngày dạy: 05/03/2018 |
|
§2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN. ĐƯỜNG XIÊN VÀ HÌNH CHIẾU |
|
|
I. MỤC TIÊU:
1. Kiến thức: Học sinh biết được khái niệm đường vuông góc, đường xiên, hình chiếu, biết vẽ hình và biết các định lý về mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.
2. Kĩ năng: Vẽ hình và so sánh hai đoạn thẳng.
3. Thái độ: Giáo dục tính chính xác, khoa học, óc tư duy sáng tạo.
4. Nội dung trọng tâm: Biết được quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, hợp tác, năng lực giải quyết vấn đề, năng lực vận dụng, năng lực giao tiếp, năng lực tư duy, năng lực tự quản lý (năng lực làm chủ bản thân)
- Năng lực chuyên biệt: Năng lực giải quyết các vấn đề toán học; năng lực tính toán; năng lực sử dụng ngôn ngữ toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Sgk, thước, bảng phụ ghi bài tập, thước đo góc, êke.
2. Học sinh: SGK, thước chia khoảng, bảng phụ, thước đo góc, êke.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Quan hệ giữa đường vuông góc và đường xiên |
Biết khái niệm đường vuông góc, đường xiên, hình chiếu |
|
|
|
2. Các đường xiên và hình chiếu của chúng |
Biết quan hệ hệ giữa đường vuông góc và đường xiên |
|
Biết vận dụng các mối quan hệ giữa đường vuông góc, đường xiên, hình chiếu để giải bài tập. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5’)
H :
Trong một bể bơi hai bạn Hùng, Dũng cùng xuất phát từ
A, Hùng bơi tới điểm H, Dũng bơi tới điểm B. biết H
và B cùng thuộc đường thẳng d, AH
:
Trong một bể bơi hai bạn Hùng, Dũng cùng xuất phát từ
A, Hùng bơi tới điểm H, Dũng bơi tới điểm B. biết H
và B cùng thuộc đường thẳng d, AH
![]() d, AB không vuông góc với d. hỏi ai bơi xa hơn? vì sao?
d, AB không vuông góc với d. hỏi ai bơi xa hơn? vì sao?
Đáp
án:
Trong
![]() AHB
có:
AHB
có:
![]() = 1v (4,0đ)
= 1v (4,0đ)
Trong tam giác vuông cạnh huyền là cạnh lớn nhất, nên AH < AB (định lí về quan hệ giữa góc và cạnh đối diện trong một tam giác) (4,0đ)
Vậy bạn Dũng bơi xa hơn bạn Hùng. (2,0đ)
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV chỉ vào hình vẽ phần KTBC giới thiệu AH là đường vuông góc, AB là đường xiên, HB là hình chiếu của đường xiên AB trên đường thẳng d. Bài học hôm nay, chúng ta sẽ tìm hiểu về mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. K/n đường vuông góc, đường xiên, hình chiếu của đường xiên (8’)
(1) Mục tiêu: HS nhận biết được khái niệm đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài 1 đường thẳng đến đường thẳng đó, khái niệm hình chiếu vuông góc của điểm, của đường xiên.
(2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi.
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Câu trả lời, kết quả thực hành ở bài toán ?1.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1
H, B d A d
Đoạn AH là đường vuông góc từ A đến d. H gọi là chân đường hay hình chiếu của A trên d. Đoạn AB là một đường xiên kẻ từ A đến d. HB là hình chiếu của đường xiên AB trên d. |
GV: Đưa ra hình vẽ và trình bày như Sgk/57 Gọi HS nhắc lại các khái niệm. Giải ?1. Cho A d. Hãy dùng ê ke để vẽ và tìm hình chiếu của điểm A trên d. Vẽ đường xiên từ A đến d, tìm hình chiếu của đường xiên này trên d.
H: Hãy so sánh AK và AM? |
HS: theo dõi ghi bài
HS: nhắc lại các khái niệm H
AK: đường vuông góc AM: đường xiên, KM: hình chiếu HS: ∆AKM vuông tại K Nên AM > AK |
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp làm chủ bản thân.
|
HOẠT ĐỘNG 3. Quan hệ giữa đường vuông góc và đường xiên (10’)
(1) Mục tiêu: Học sinh nhận biết được quan hệ giữa đường vuông góc và đường xiên
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải bài toán ?2, 3 và nội dung định lý 1.
2. Quan hệ giữa đường vuông góc và đường xiên
Định lý 1: Sgk/58
Chứng minh: AHB,
có
AB là cạnh lớn nhất. Nên suy ra AB > AH Độ dài đường vuông góc AH gọi là khoảng cách từ điểm A đến đường thẳng d. |
Bài tập ?2 đề bài đưa lên bảng phụ
H: Hãy so sánh độ dài của đường vuông góc và các đường xiên ? H: Các em rút ra kết luận gì ? Gọi HS đọc định lý 1 Em nào có thể chứng minh được định lý trên ? H: Định lý nêu rõ mối quan hệ giữa các cạnh trong vuông là định lý nào ? Hãy phát biểu định lý Pytago và dùng định lý này để chứng minh AB > AH |
Từ 1 điểm A ta chỉ kẻ được 1 đường thẳng và vô số đường xiên đến d Đường vuông góc ngắn hơn đường xiên HS : đọc định lý 1 HS: vẽ hình ghi GT, KL HS: Định lý Pytago
HS: phát biểu và chứng minh AHB
có
AB2 = AH2+HB2 AB2 > AH2 AB > AH |
Năng lực sử dụng ngôn ngữ toán học, sử dụng các công thức tổng quát |
HOẠT ĐỘNG 4. Các đường xiên và hình chiếu của chúng (10’)
(1) Mục tiêu: Học sinh nắm được quan hệ giữa đường xiên và hình chiếu.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải bài toán ?4 và nội dung định lý 2.
3. Các đường xiên và hình chiếu của chúng : ?
Xét AHB vuông tại H có: AB2 = AH2 + HB2 (định lý Py-ta-go). Xét AHC vuông tại H có: AC2 = AH2 + HC2 (định lý Py-ta-go) a) Có HB > HC (gt) HB2 > HC2 AB2 > AC2 AB > AC. b) Có AB > AC (gt) AB2 > AC2 HB2 > HC2 HB > HC. c) Có HB = HC (gt) HB2 = HC2 AH2 + HB2 = AH2 + HC2 AB2 = AC2 AB = AC. * Định lý 2: SGK/59. |
Bài ?4 H.10 (đề bài đưa lên bảng phụ) GV gọi HS lên bảng giải H: HB, HC là gì ? Hãy sử dụng định lý Pytago suy ra rằng : a) Nếu HB > HC AB > AC
b) Nếu AB > AC HB > HC
c) HB = HC thì AB = AC và ngược lại
Từ bài toán trên hãy suy ra quan hệ giữa các đường xiên và hình chiếu của chúng (nội dung định lý 2 treo bảng phụ) |
HS: đọc to đề bài ?4
1 HS lên bảng giải - Là hình chiếu của AB, AC trên d AHB có AB2 = AH2+ HB2 (pytago) AHC có AC2 = AH2 + AC2 (pytago) a) Có HB > HC (gt) AB2 > HC2 AB2 > AC2 b) có AB > AC (gt) AB > AC AB2 > AC2 HB2 > HC2 HB > HC c)
HB = HC
HB2
= HC2
AH2
+ HB2
=
HS: nhắc lại |
Tư duy, vận dụng.
Tư duy, vận dụng.
|
C. LUYỆN TẬP, VẬN DỤNG (9’)
(1) Mục tiêu: Củng cố cho học sinh kiến thức về quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vận dụng giải được các bài tập.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài tập 1, 2.
Chuyển giao: Yêu cầu HS làm bài tập: Bài 1: Cho hình vẽ. Biết rằng AB < AC. Trong các kết luận sau sau, kết luận nào đúng? Tại sao? a) HB = HC b) HB > HC c) HB < HC Bài
2: Cho hình chữ
nhật ABCD các đường chéo AD và BC.
So sánh: AB và BD; AD và AC. Xác định khoảng cách từ điểm D đến đường thẳng BC. |
HS thảo luận nhóm đôi
Đáp án: C HS: hoạt động theo nhóm làm bài ABCD là hình chữ nhật nên AB AD nên AB là đường vuông góc, BD là đường xiên kẻ từ điểm B đến đường thẳng AD AB < BD (Quan hệ giữa đường vuông góc và đường xiên) Tương tự: AD < AC - DC BC tại C nên DC là khoảng |
Năng lực giao tiếp, hợp tác, làm chủ bản thân
|
D. HƯỚNG DẪN VỀ NHÀ (2’)
- Học bài nắm vững các định lý quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- BTVN: 8, 9, 10, 11 (SGK) và 11, 12 (SBT). Chuẩn bị bài tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Các bài tập củng cố thể hiện trong "Hoạt động luyện tập, vận dụng" (MĐ 1, 3).
Tuần: 26 Tiết KHGD: 51 |
Ngày soạn: 04/03/2018 Ngày dạy: 07/03/2018 |
LUYỆN TẬP
I. MỤC TIÊU
1. Kiến thức: Củng cố các định lý quan hệ giữa đường vuông góc và đường xiên, giữa đường xiên và hình chiếu của chúng.
2. Kĩ năng: Rèn luyện kỹ năng vẽ hình theo yêu cầu đề bài, tập phân tích để chứng minh bài toán, biết chỉ ra căn cứ của các bước chứng minh
3. Thái độ: Giáo dục ý thức vận dụng kiến thức vào thực tiễn.
4. Nội dung trọng tâm của bài: Củng cố các định lý quan hệ giữa đường vuông góc và đường xiên, giữa đường xiên và hình chiếu của chúng.
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, năng lực hợp tác, năng lực giải quyết vấn đề, năng lực sáng tạo, năng lực giao tiếp, năng lực tư duy, năng lực tự quản lý (năng lực làm chủ bản thân).
- Năng lực chuyên biệt: Năng lực giải quyết các vấn đề toán học; năng lực tính toán; năng lực sử dụng ngôn ngữ toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ, thước thẳng, compa, thứơc đo góc, giáo án.
2. Học sinh: Bảng nhóm, thước thẳng, compa, thứơc đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Quan hệ giữa đường vuông góc và đường xiên. |
|
Hiểu quan hệ giữa đường vuông góc và đường xiên |
Biết vận dụng các mối quan hệ giữa đường vuông góc và đường xiên để giải bài tập. |
Sử dụng định lý trong các bài toán thực tế. |
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (10')
H S1:
Phát biểu định lý 2 về quan hệ giữa đường xiên và
hình chiếu (HS phát biểu như SGK).
S1:
Phát biểu định lý 2 về quan hệ giữa đường xiên và
hình chiếu (HS phát biểu như SGK).
Chữa bài tập 11 tr 25 SBT.
Đáp án: Có AB < AC (định lý 1)
B
C
AC < AD < AE (định lý 2, quan hệ đường xiên, hình chiếu).
V ậy
AB < AC < AD < AE. (10đ)
ậy
AB < AC < AD < AE. (10đ)
HS2: Chữa bài tập 11 tr 60 SGK.
C
Đáp án: Có BC < BD C nằm giữa B và D.
Xét
ABC
(![]() = 1V)
= 1V)
![]() nhọn. Mà
nhọn. Mà
![]() và
và
![]() kề bù
kề bù
![]() tù
tù
Xét
ACD
có
![]() tù
tù
![]() nhọn
nhọn
![]() >
>![]()
AD > AC (quan hệ giữa góc) (10đ)
AD > AC (quan hệ giữa góc) (10đ)
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Ở tiết học trước các em đã được biết quan hệ giữa đường vuông góc và đường xiên, giữa đường xiên và hình chiếu của chúng. Tiết học hôm nay các em sẽ được củng cố các định lý về giữa đường vuông góc và đường xiên, giữa đường xiên và hình chiếu của chúng. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 2. Luyện tập (25’)
(1) Mục tiêu: Biết vận dụng các mối hệ giữa đường vuông góc và đường xiên, giữa đường xiên và hình chiếu của chúng để ứng dụng vào bài cụ thể.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài toán.
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
1) Bài tập 10 Sgk/59:
GiảiTừ A ta hạ AH BC ; BH, MH lần lượt là hình chiếu của AB, AM trên đường thẳng BC. Nếu M B (hoặc C) thì AM = AB = AC. Nếu M H thì AM = AH < AB (ĐLý 1) Nếu M ở giữa B, H (hoặc C và H) thì MH < BH (MH < CH) AM < BA. Vậy trong mọi trường hợp ta đều có AM AB 2 g DAB; EAC k b) DE < BC
Chứng minh: a)
ABE
vuông tại A nên
Mà
Trong
BEC
có cạnh BC đối diện với
b)
ADE
vuông tại A nên
Mà
Trong
BDE
có cạnh BE đối diện với
Từ (1) và (2) suy ra DE < BC (đpcm) 3) Bài tập 13/25 SBT:
Giải:Từ A hạ AH BC. * Xét AHB và AHC có:
AH cạnh chung AB = AC (gt) AHB = AHC (ch.cgv).
* Xét vuông AHB có: AH2 = AB2 - HB2 (ĐL Py -ta-go) AH2 = 102 - 62 = 100 -36 = 64. AH = 8cm. Vì bán kính cung tròn tâm A lớn hơn khoảng cách từ A tới đường thẳng BC nên cung tròn (A, 9cm) cắt đường thẳng BC tại hai điểm D và E. |
GV: Cho học sinh đọc nội dung bài tập 10/59.
GV hãy xét từng vị trí của M để chứng minh AM AB
GV: Yêu cầu đọc nội dung bài 13/60?
H: Em nào có thể chứng minh được BE < BC ? GV: Làm như thế nào để chứng minh được DE < BC ? Hãy xét các điểm EB, ED kẻ tại E đến đoạn thẳng AB ? GV nhận xét, hoàn chỉnh
GV: Đọc nội dung bài 13/25 SBT (đề bài trên bảng phụ) vì ABC có AB = AC = 10cm ; BC = 12 cm Cung tròn tâm A bán kính 9cm có cắt đường thẳng BC không ? Vì sao ? Gợi ý : Hạ AH BC. Hãy tính AH ? Vậy làm thế nào để tính được khoảng cách từ A đến BC? Từ đó ta có kết luận gì về cung tròn tâm A bán kính 9 cm? GV: Hướng dẫn trình bày.
|
HS: đọc đề bài, vẽ hình, ghi GT, KL
HS: lên bảng giải Từ A hạ AH BC, AH khoảng cách từ A đến BC M B ( C) M H M ở giữa B, H (C, H)
HS: đọc đề bài, lên bảng vẽ hình, ghi GT, KL
HS: Thảo luận nhóm trả lời
HS: chứng minh
HS: nhận xét
HS: Một em vẽ hình và ghi gt, kl.
HS: Tiến hành làm theo hướng dẫn
HS: cả lớp làm vào vở bài tập |
Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
|
C. LUYỆN TẬP: Đã thực hiện ở mục B
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG
HOẠT ĐỘNG 3. Thực hành (8’)
(1) Mục tiêu: Vận dụng kiến thức đã học vào thực tế.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp, thực hành, trực quan/ kỹ thuật động não.
(3) Hình thức tổ chức hoạt động: Hoạt động nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Bài làm của học sinh.
Bài tập 12 tr 60 SGK
Cho a// b, đoạn thẳng AB vuông góc với 2 đường thẳng a, b độ dài đoạn AB là khoảng cách giữa 2 đường thẳng đó. Chiều rộng tấm gỗ là khoảng cách giữa 2 cạnh song song Muốn đo chiều rộng miếng gỗ ta phải đặt thước vuông góc với 2 cạnh song song của nó.
|
+ Chuyển giao: Bài tập 12 tr 60 SGK (treo bảng phụ)Cho đường thẳng a // b, thế nào là khoảng cách giữa hai đường thẳng song song. Một tấm gỗ xẻ (miếng bìa) có 2 cạnh song song. Chiều rộng của tấm gỗ là gì? Muốn đo chiều rộng tấm gỗ phải đặt thước như thế nào? Hãy đo bề rộng miếng gỗ của nhóm và cho số liệu thực tế |
HS: hoạt động nhóm thực hành bài tập 12 tr60
Mỗi nhóm 1 bảng, bút, thước chia khoảng, 1 miếng gỗ, có 2 cạnh song song.
Đại diện nhóm lên bảng trình bày
|
Giao tiếp, làm chủ bản thân.
|
E. HƯỚNG DẪN VỀ NHÀ (1’)
Ôn lại các định lý trong §1; §2. BTVN: 14 tr 60 SGK; 15; 17 SBT.
BT bổ sung: Cho ABC có AB = 4c,. AC = 5cm, BC = 6cm.
a) So sánh các góc của ABC
b) Kẻ AH BC (H BC). So sánh AB và BH, AH và HC
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
GV: Củng cố bài lồng ghép vào quá trình luyện tập.
Các bài tập củng cố thể hiện trong "Hoạt động 2, 3". (MĐ2, 3, 4)
Tuần: 27 Tiết KHGD: 52 |
Ngày soạn: 10/03/2018 Ngày dạy: 12/03/2018 |
|
§3. QUAN HỆ GIỮA BA CẠNH CỦA MỘT TAM GIÁC. BẤT ĐẲNG THỨC TAM GIÁC |
|
|
I. MỤC TIÊU:
1. Kiến thức: HS nắm vững quan hệ giữa độ dài 3 cạnh của tam giác, từ đó biết được 3 đoạn thẳng có độ dài như thế nào thì không thể là 3 cạnh của một tam giác.
HS hiểu cách chứng minh định lí bất đẳng thức tam giác dựa trên quan hệ cạnh và góc trong một tam giác.
2. Kĩ năng: Bước đầu biết vận dụng bất đẳng thức tam giác để giải toán.
3. Thái độ: Rèn tư duy logic, chính xác và khoa học. Yêu thích bộ môn.
4. Xác định nội dung trọng tâm của bài: Biết quan hệ giữa độ dài 3 cạnh của tam giác. Biết vận dụng bất đẳng thức tam giác để giải toán.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, gqvđ, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ ghi định lí, nhận xét, bất đẳng thức về quan hệ 3 cạnh của tam giác và bài tập. Thước thẳng, êke, compa, phấn màu
2. Học sinh: Ôn qui tắc chuyển vế trong bất đẳng thức. Thước thẳng, êke, compa, phấn màu
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Bất đẳng thức tam giác |
Biết được bất đẳng thức tam giác |
Hiểu cách chứng minh bất đẳng thức tam giác. |
|
|
2. Hệ quả của bất đẳng thức tam giác |
|
|
Vận dụng hệ quả của bất đẳng thức tam giác. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
*
Kiểm
tra bài cũ:
(7’)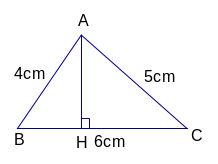
HS1: Vẽ tam giác ABC có AB = 4cm; AC = 5cm, BC = 6cm ........3đ
a) So sánh các góc tam giác ABC
Ta
có: AB < AC < BC suy ra:
![]() ………………………… 4đ
………………………… 4đ
b)
Kẻ AH
![]() BC ( H
BC ( H
![]() BC). So sánh AB và BH , AC và HC.
BC). So sánh AB và BH , AC và HC.
Ta có: AB > BH ; AC > HC ………………………….............. 3đ
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Câu trả lời của Hs
Hoạt động của GV |
Hoạt động của HS |
GV: Từ kết quả phần KTBC em có nhận xét gì về tổng độ dài 2 cạnh bất kì của tam giác ABC so với độ dài cạnh còn lại? GV: Ta hãy xét xem nhận xét này có đúng với mọi tam giác hay không? Đó là nội dung bài học hôm nay chúng ta sẽ tìm hiểu về mối quan hệ giữa độ dài 3 cạnh của một tam giác. Bất đẳng thức tam giác. |
HS: Trong độ dài 2 cạnh bất kì của tam giác lớn hơn độ dài cạnh còn lại của tam giác ABC (4 + 5 > 6; 4 + 6 > 5; 6 + 5 > 4) HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||||||
HOẠT ĐỘNG 2. Bất đẳng thức tam giác. (18’) (1) Mục tiêu: HS nhận biết được quan hệ giữa độ dài ba cạnh của một tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp (4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập. (5) Sản phẩm: Lời giải bài toán ?1, ?2 và nội dung định lý. |
|||||||||
1. Bất đẳng thức tam giác
Định lí (Sgk/61)
GT
KL
AB
+ AC > BC AB
+ BC > AC AC
+ BC > AB
Chứng minh - Trên tia đối của tia AB lấy điểm D sao cho AD = AC. Nối CD Có BD = BA +AC - Có A nằm giữa B và D nên tia CA nằm giữa 2 tia CB và CD nên
-
Mà
|
GV:
Yêu cầu HS thực hiện
GV: Hãy thử vẽ tam giác với các cạnh có độ dài: a) 1cm, 2cm, 4cm b) 1cm, 3cm, 4cm H: Em có nhận xét gì? H: có 1 +2 < 4; 1+ 3 = 4 Vậy trong mỗi trường hợp, tổng độ dài 2 cạnh nhỏ so với đoạn lớn nhất như thế nào? GV: Như vậy, không phải 3 độ dài nào cũng là độ dài 3 cạnh của 1 tam giác. Ta có định lí sau. H: Hãy cho biết GT và KL của định lí? GV: Ta sẽ chứng minh bất đẳng thức đầu tiên H: Làm thế nào để tạo ra 1 tam giác có 1 cạnh là BC, một cạnh bằng AB + AC để so sánh chúng? GV hướng dẫn HS phân tích.
H: Làm thế nào để chứng minh BD > BC
H:
Tại sao
H:
GV: Các bất đẳng thức còn lại chứng minh tương tự, ta có: AB + BC > AC AC + BC > AB đó là nội dung bài tập 29.Sgk/64 GV: Giới thiệu các bất đẳng thức ở phần KL của định lí được gọi là bất đẳng thức tam giác. |
HS
thực hiện
HS cả lớp làm vào vở 1HS lên bảng thực hiện
HS: Không vẽ được tam giác có độ dài các cạnh như vậy HS: Vậy tổng độ dài 2 đoạn nhỏ, nhỏ hơn hoặc bằng độ dài đoạn lớn nhất
HS: Đọc định lí
HS vẽ hình và ghi GT, KL của định lí
-Trên tia đối của tia AB lấy điểm D sao cho AD = AC. Nối CD, Có BD = BA + AC HS nghe GV hướng dẫn HS phân tích: HS:
Muốn chứng minh BD > BC ta cần có
HS:
Có A nằm giữa B và D nên tia CA nằm giữa 2 tia CB và
CD nên
-
Mà
HS trình bày miệng bài toán
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
|
||||||
HOẠT ĐỘNG 3. Hệ quả của bất đẳng thức tam giác. (9’) (1) Mục tiêu: HS nhận biết được 3 đoạn thẳng có độ dài như thế nào thì không thể là ba cạnh của một tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp (4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập. (5) Sản phẩm: Vận dụng hệ quả của bất đẳng thức tam giác. |
|||||||||
2. Hệ quả của bất đẳng thức tam giác
Từ các bất đẳng thức suy ra: AB > AC – BC; AB > BC – AC; AC > AB – BC; AC > BC – AB; BC > AC – AB; BC > AB – AC;
* Hệ quả: SGK/62.
* Nhận xét: SGK/62.
AB – BC < AC < AB + BC AC – BC < AB < AC + BC AB – AC < BC < AB + AC
Lưu ý: SGK/63. |
GV: Hãy nêu lại các bất đẳng thức tam giác.
GV: Phát biểu qui tắc chuyển vế của BĐT GV: Yêu cầu học sinh viết 3 bất đẳng thức tam giác. Dùng quy tắc chuyển vế ta được hệ quả. Hãy phát biểu hệ quả này bằng lời Kết hợp với các bất đẳng thức tam giác, ta có: AC – AB < BC < AB + AC Hãy phát biểu nhận xét trên bằng lời Hãy điền và dấu …. trong các bất đẳng thức … < AB < … … < AC < … Yêu
cầu HS làm
Cho HS đọc phần lưu ý |
HS:
Trong
AB + AC > BC; AB + BC > AC; AC + BC > AB HS phát biểu qui tắc
HS: BC-AC < AB < BC+AC BC-AB < AC < BC+AB
Phát biểu hệ quả này bằng lời
HS phát biểu nhận xét trên bằng lời
HS trả lời miệng.
HS: không có tam giác với 3 cạnh dài 1cm, 2cm, 4cm vì 1+ 2 < 4 HS đọc phần lưu ý |
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân. |
||||||
C. LUYỆN TẬP, CỦNG CỐ (8’)
(1) Mục tiêu: Củng cố kiến thức về bất đẳng thức tam giác. Hs vận dụng để giải được các bài tập ở các mức độ NB, TH, VD.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài tập 1, 2, 3.
+ Chuyển giao: GV: Yêu cầu HS làm bài tập Bài 1: Cho tam giác MNP khi đó MN + NP > PM và MP – MN < NP. Hãy điền dấu >, < thích hợp vào chỗ trống MP + NP … MN; MN – MP … PN Bài 2: 1) Có hay không một ∆ mà độ dài 3 cạnh của nó tương ứng là 2cm; 3cm; 6cm? Vì sao? 2) Bộ ba đoạn thẳng nào không thể là ba cạnh của một tam giác: a) 2cm ; 3cm ; 6cm b) 2cm ; 4cm ; 6cm c) 3cm ; 4cm ; 6cm 3) Bạn Lan nói: Muốn biết độ dài ba đoạn thẳng nào đó có tương ứng là độ dài ba cạnh của một ∆ hay không ta chỉ cần so sánh độ dài lớn nhất với tổng hai độ dài còn lại hoặc so sánh độ dài nhỏ nhất với hiệu hai độ còn lại. Theo em bạn Lan nói đúng hay không vì sao? Bài 3: Cho tam giác ABC có AH BC tại H. So sánh AB và BH; AC và CH Từ đó hãy nêu một cách khác để chứng minh bất đẳng thức tam giác.
|
HS: Thảo luận nhóm làm bài
1) Không vì 2 + 3 < 6
2) 2cm ; 3cm ; 6cm 2cm ; 4cm ; 6cm
3) Bạn Lan nói đúng vì bạn đã vận dụng theo Bất đẳng thức tam giác về hệ quả của nó
AB > BH AC > CH AB + AC > BH + CH = BC |
Năng lực tư duy, vận dụng, giao tiếp, làm chủ bản thân, hợp tác. |
D. HƯỚNG DẪN VỀ NHÀ (2’)
- Nắm vững bất đẳng thức tam giác, học cách chứng minh định lí bất đẳng thức tam giác
- BTVN: 16, 17, 18, 19 Sgk/63
- Tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Bài 1 (MĐ1); Bài 2 (MĐ2); Bài 3 (MĐ3)
Tuần: 27 Tiết KHGD: 53 |
Ngày soạn: 10/03/2018 Ngày dạy: 14/03/2018 |
LUYỆN TẬP
I. MỤC TIÊU
1. Kiến thức: Củng cố quan hệ giữa ba cạnh của một tam giác. Biết vận dụng quan hệ này để xét xem ba đoạn thẳng cho trước có thể là ba cạnh của một tam giác hay không.
2. Kĩ năng: Rèn luyện kĩ năng vận dụng quan hệ giữa ba cạnh của một tam giác để chứng minh bài toán và vào thực tế đời sống.
3. Thái độ: Thấy được sự ứng dụng của toán học trong đời sống.
4. Xác định nội dung trọng tâm của bài: Củng cố quan hệ giữa ba cạnh của một tam giác.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, phấn màu, com pa, phiếu học tập.
2. Học sinh: Ôn tập quan hệ giữa ba cạnh của tam giác. Bảng nhóm, thước thẳng, compa.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Quan hệ giữa ba cạnh của tam giác. |
Biết quan hệ giữa độ dài ba cạnh của tam giác. |
Hiểu cách chứng minh bất đẳng thức tam giác. |
Biết vận dụng quan hệ giữa độ dài ba cạnh của tam giác để giải bài toán. |
Sử dụng định lý trong các bài toán thực tê. |
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (7')
HS1: Phát biểu nhận xét quan hệ ba cạnh của một tam giác. Minh hoạ bằng hình vẽ và ghi bất đẳng thức.
T rả
lời:
Trong
một tam giác, độ dài một cạnh bao giờ cũng lớn hơn
hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn
lại .........……….4đ
rả
lời:
Trong
một tam giác, độ dài một cạnh bao giờ cũng lớn hơn
hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn
lại .........……….4đ
BC –AC < AB < BC + AC ..........……….2đ
BC – AB < AC < BC + AB ……….2đ
AC – AB < BC < AB + AC ……….2đ
HS2: Làm bài tập 16 Sgk/63.
Đáp án: Có AC – BC < AB < AC + BC .........................3đ
Hay 7 – 1 < AB < 7 + 1
6 < AB < 8 .........................2đ
Mà
độ dài AB là một số nguyên
![]() AB = 7cm .........................2đ
AB = 7cm .........................2đ
Do đó tam giác ABC cân tại A. .........................3đ
Gv nhận xét và cho điểm.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Ở tiết học trước các em đã được biết quan hệ giữa ba cạnh của một tam giác. Tiết học hôm nay các em sẽ được củng cố kiến thức về quan hệ giữa ba cạnh của một tam giác thông qua giải một số bài tập. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
HOẠT ĐỘNG 2. Luyện tập (27’) (1) Mục tiêu: HS vận dụng quan hệ giữa ba cạnh của một tam giác để giải bài toán liên quan đến tính thực tế. (2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi (3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp (4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập. (5) Sản phẩm: Lời giải các bài toán. |
|||
1. Bài 18. Sgk/63 a) 2cm; 3cm; 4cm Vì 4cm < 2cm + 3cm => Vẽ được tam giác với độ dài ba đoạn thẳng trên. b) 1cm; 2cm; 3,5cm Ta có: 3,5cm > 1cm + 2cm => Không vẽ được tam giác với độ dài ba đoạn thẳng là 1cm; 2cm; 3,5cm c) 2,2cm; 2cm; 4,2cm Vì 4,2cm = 2cm + 2,2cm Nên không vẽ được tam giác với độ dài ba đoạn thẳng là 2,2cm; 2cm; 4,2cm
2. Bài 19. Sgk/63: Gọi độ dài cạnh thứ ba của tam giác cân là x (cm). Theo bất đẳng thức tam giác ta có: 7,9 – 3,9 < x < 7,9 + 3,9. 4 < x < 11,8
Chu
vi của tam giác cân là:
3. Bài 21. Sgk/64: Tam giác ABC, có: AC + CB > AB (bđt tam giác) Nên AC + CB ngắn nhất khi AC + CB = AB Hay điểm C nằm giữa hai điểm A và B Khi đó 3 điểm A, B, C thẳng hàng Phải dựng cột điện tại điểm C thuộc đường thẳng AB (bên bờ sông gần khu dân cư) để độ dài đường dây dẫn là ngắn nhất. |
GV: Nêu bài 18 Sgk (đưa đề bài lên bảng phụ) H: Muốn biết độ dài ba đoạn thẳng có phải là ba cạnh của một tam giác hay không ta làm như thế nào? GV: Yêu cầu Hs làm bài trên vở nháp Sau 2’ giáo viên thu một vài bài chấm điểm và gọi Hs lên bảng trình bày. GV: Yêu cầu Hs dưới lớp nhận xét. Giáo viên uốn nắn sửa theo đáp án GV: nêu bài 19 tr63 Sgk H: chu vi của tam giác là gì? H: Vậy trong hai cạnh dài 3,9 cm và 7,9 cm , cạnh nào sẽ là cạnh thứ ba, cạnh nào sẽ là cạnh bên của tam giác cân? Làm thế nào để biết ? GV: yêu cầu HS tính chu vi tam giác cân. GV: nêu bài 21 (đưa đề bài và hình vẽ lên bảng phụ), giới thiệu trạm biến áp A, khu dân cư B, cột điện C. H: Cột điện C ở vị trí nào để độ dài AB ngắn nhất?
|
HS: Đọc đề bài 18 Sgk. HS: Đứng tại chỗ trả lời
HS: Thảo luận làm bài theo nhóm
Hs lên bảng trình bày.
HS: Nhận xét
HS: Trả lời là tổng ba cạnh của tam giác đó. HS: dựa vào bất đẳng thức tam giác
HS: trình bày cách xác định cạnh của tam giác cân. HS: tính chu vi tam giác HS: quan sát đề bài trên bảng thảo luận và trình bày
HS: Vị trí cột điện C là giao của bờ sông với đường thẳng AB
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
|
C. LUYỆN TẬP: Đã thực hiện ở mục B
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG
HOẠT ĐỘNG 3. Tìm tòi, mở rộng (8’)
(1) Mục tiêu: Giúp HS tăng cường ý thức tự tìm hiểu, mở rộng kiến thức và sự hiểu biết của mình thông qua các câu hỏi thực tiễn.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp, thực hành, trực quan/ kỹ thuật động não.
(3) Hình thức tổ chức hoạt động: Hoạt động nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Các tư liệu mà học sinh sưu tầm được liên quan đến các yếu tố trong tam giác
*Bài tập 22. Sgk/64:
ABC, có: 90 – 30 < BC < 90 + 30 Hay 60 < BC < 120 a) Nếu đặt máy phát ở C với bán kính hoạt động là 60 km thì thành phố B không nhận được tín hiệu. b) Nếu đặt máy phát ở C với bán kính hoạt động là 120 km thì thành phố B nhận được tín hiệu. |
+ Chuyển giao: Bài tập (treo bảng phụ)H: Bài tập 22 cho ta biết và yêu cầu chứng minh điều gì? H: Muốn biết ba tỉnh có nhận được tín hiệu hay không thì ta cần chỉ ra khoảng cách giữa ba thành phố phải nhỏ hơn bán kính phát sóng. Vậy có kết luận gì?
|
HS: Hoạt động nhóm, đại diện trả lời. |
Năng lực sáng tạo, làm chủ bản thân.
|
E. HƯỚNG DẪN VỀ NHÀ (2’)
- Học thuộc quan hệ giữa ba cạnh của một tam giác thể hiện bằng bất đẳng thức tam giác.
- Xem các bài tập đã giải. BTVN 25, 27, 29, 30/26 – 27 SBT.
- Tiết sau học “Tính chất ba đường trung tuyến của tam giác”, mỗi HS chuẩn bị một tam giác bằng giấy và một mảnh giấy kẻ ô vuông mỗi chiều 10 ô như hình 22 tr 65 Sgk. Mang compa, thước thẳng có chia khoảng.
- Ôn khái niệm trung điểm của đoạn thẳng và cách xác định trung điểm đoạn thẳng bằng thước và cách gấp giấy.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
GV: Củng cố bài lồng ghép vào quá trình luyện tập.
Các bài tập củng cố thể hiện trong "Hoạt động 2, 3". (MĐ2, 3, 4)
Tuần: 28 Tiết KHGD: 54 |
Ngày soạn: 15/03/2018 Ngày dạy: 17/03/2018 |
|
§4. TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC |
|
|
I. MỤC TIÊU:
1. Kiến thức: HS nắm được khái niệm đường trung tuyến (xuất phát từ một đỉnh hoặc ứng với một cạnh) của tam giác và nhận thấy mỗi tam giác có ba đường trung tuyến.
2. Kĩ năng: Luyện kỹ năng về các đường trung tuyến của một tam giác. Thông qua thực hành cắt giấy và vẽ hình trên giấy kẻ ô vuông phát hiện ra tính chất ba đường trung tuyến của tam giác, hiểu khái niệm trọng tâm của tam giác. Biết sử dụng tính chất ba đường trung tuyến của một tam giác để giải một số bài tập đơn giản.
3. Thái độ: Cẩn thận, chính xác.
4. Xác định nội dung trọng tâm của bài: Nắm được khái niệm đường trung tuyến, và nhận thấy mỗi tam giác có ba đường trung tuyến.
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, năng lực hợp tác, năng lực giải quyết vấn đề, năng lực vận dụng, năng lực giao tiếp, năng lực tư duy, năng lực tự quản lý (làm chủ bản thân).
- Năng lực chuyên biệt: Năng lực giải quyết các vấn đề toán học; năng lực tính toán; năng lực sử dụng ngôn ngữ toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ ghi bài tập, định lý, phiếu học tập của học sinh. Một tam giác bằng giấy để gấp hình, một giấy kẻ ô vuông mỗi chiều 10 ô gắn trên bảng phụ (hình 22 Sgk/65), một tam giác bằng bìa, Thước thẳng, compa, thước đo góc.
2. Học sinh: Mỗi em có một tam giác bằng giấy kẻ ô vuông, mỗi chiều 10 ô. Bảng nhóm, thước thẳng, compa, thứơc đo góc. Ôn lại khái niệm trung điểm của đoạn thẳng và cách xác định trung điểm của đoạn thẳng bằng thước thẳng hoặc gấp giấy.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Đường trung tuyến của tam giác |
Nhận
biết được đường trung tuyến của
Biết
vẽ 3 đường trung tuyến của
|
|
|
|
2. Tính chất ba đường trung tuyến của tam giác |
Biết
3 đường trung tuyến của
|
Trọng tâm cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó |
Vận dụng lý thuyết giải các dạng bài tập trắc nghiệm
|
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (7’)
H: Trung điểm của đoạn thẳng là gì?
Nêu cách xác định trung điểm của một đoạn thẳng bằng thước?
(HS trả lời như Sgk tập 1 lớp 6)
Gv nhận xét, cho điểm
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Câu trả lời của Hs
Hoạt động của GV |
Hoạt động của HS |
Gv: Ở lớp 6 ta đã biết về trung điểm của một đoạn thẳng, vậy trong 1 tam giác nếu ta nối từ đỉnh đến trung điểm của cạnh đối diện thì đoạn thẳng đó được gọi là gì và có tính chất đặc biệt gì ta sẽ nghiên cứu bài học hôm nay. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||
Hoạt động 2: Đường trung tuyến của tam giác. (9’) (1) Mục tiêu: HS được khái niệm đường trung tuyến trong tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS biết cách vẽ và nắm được khái niệm đường trung tuyến của tam giác. |
|||||
1. Đường trung tuyến của tam giác:
Đoạn thẳng AM nối đỉnh A của ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của ABC Đôi khi, đường thẳng AM cũng gọi là đường trung tuyến của ABC. Mỗi có ba đường trung tuyến |
GV Vẽ ABC, xác định trung điểm của M (bằng thước thẳng) nối đoạn thẳng AM rồi giới thiệu đoạn thẳng AM là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC GV: Tương tự, hãy vẽ trung tuyến xuất phát từ đỉnh B, từ C của ABC H: Vậy một có mấy đường trung tuyến ? GV nhấn mạnh: Đường trung tuyến của là đoạn thẳng nối từ đỉnh của tới trung điểm cạnh đối diện. Mỗi có ba đường trung tuyến. Đôi khi đường thẳng chứa trung tuyến cũng gọi là đường trung tuyến của H: Em có nhận xét gì về vị trí ba đường TT của GV: Chúng ta sẽ kiểm nghiệm lại nhận xét này thông qua các thực hành sau |
HS: vẽ hình vào vở theo sự hướng dẫn của GV HS: nghe GV giới thiệu về đường trung tuyến của tam giác
1HS lên bảng vẽ tiếp vào hình đã có
HS: Một có ba đường trung tuyến
HS: nghe GV trình bày
HS: Ba đường trung tuyến của ABC cùng đi qua một điểm
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, giao tiếp làm chủ bản thân.
|
||
Hoạt động 3: Tính chất ba đường trung tuyến của tam giác. (18’) 1) Mục tiêu: HS hiểu được tính chất các đường trung tuyến trong tam giác (2) Phương pháp/Kĩ thuật dạy học: Thu thập thông tin, thực hành, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp (4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập (5) Sản phẩm: HS nắm được tính chất ba đường trung tuyến trong tam giác. |
|||||
2. Tính chất ba đường trung tuyến của tam giác: a
?3 AD là đường trung tuyến của ABC. Ta
có:
b) Tính chất: Định lý: Sgk/66
- Điểm G gọi là trọng tâm của tam giác. |
Thực hành 1: (Sgk) GV yêu cầu HS thực hành theo hướng dẫn của Sgk rồi trả lời ?2 GV quan sát HS thực hành rồi uốn nắn Thực hành 2: (Sgk) GV yêu cầu HS thực hành theo hướng dẫn của Sgk GV y/c HS nêu cách xác định các trung điểm E và F của AC và AB. H: Giải thích tại sao khi xác định như vậy thì E lại là trung điểm của AC ? GV: Tương tự, F là trung điểm của AB GV yêu cầu HS thực hành theo Sgk rồi trả lời ?3 H: Qua các thực hành trên em có nhận xét gì về tính chất ba đường trung tuyến của một tam giác ? GV yêu cầu HS nhắc lại định lý GV giới thiệu điểm G gọi là trọng tâm của |
HS: Toàn lớp lấy đã chuẩn bị sẵn thực hành theo Sgk rồi trả lời câu hỏi ?2 HS: toàn lớp vẽ ABC trên giấy kẻ ô vuông như hình 22 (Sgk) Một HS lên bảng thực hiện trên bảng phụ có kẻ ô vuông GV đã chuẩn bị sẵn
HS: Chứng minh AHE = CKE.
HS: C.minh tương tự
HS: Vận dụng làm ?3
HS: phát biểu định lý Sgk/66
Một vài HS nhắc lại định lý |
Tư duy, vận dụng, giải quyết vấn đề, giao tiếp làm chủ bản thân.
|
||
C. LUYỆN TẬP, CỦNG CỐ (8’)
(1) Mục tiêu: Vận dụng tính chất đường trung tuyến trong tam giác vào bài tập
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp.
(3) Hình thức tổ chức hoạt động: Cá nhân, hoạt động nhóm.
(4) Phương tiện dạy học: Bảng phấn, SGK.
(5) Sản phẩm: Bài làm của học sinh
+ Chuyển giao: GV: Em hãy nhắc lại tính chất của ba đường trung tuyến trong tam giác. - GV: Yêu cầu HS làm bài tập 23 sgk. -GV: Yêu cầu HS làm bài tập 24 sgk trên phiếu học tập bằng cách hoạt động nhóm
|
Hs: Nhắc lại tính chất
Hs: Nghiên cứu bài tập rồi trả lời.
HS: Hoạt động nhóm làm bài tập và nêu kết quả. a)
MG =
b)
NS =
|
Năng lực tư duy, vận dụng, giao tiếp, làm chủ bản thân, hợp tác. |
D
 .
TÌM TÒI, MỞ RỘNG
.
TÌM TÒI, MỞ RỘNG
GV: Yêu cầu HS tìm hiểu thêm
+ Đặt miếng bìa hình tam giác lên giá nhọn, điểm đặt cho miếng bìa
đó nằm thăng bằng chính là trọng tâm của tam giác. (H.a)
+ Người ta ứng dụng điều này vào việc làm chiếc diều hình tam giác.
Để diều có thể cân thăng bằng và bay lên được người ta phải buộc dây nối vào chính trọng tâm tam giác. (H.b)
HS về nhà làm thử và giải thích ứng dụng này
E. HƯỚNG DẪN VỀ NHÀ (2’)
- Học thuộc định lý ba đường trung tuyến của tam giác.
- Làm bài tập: 25; 26; 27 Sgk/67. Tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Hãy nhắc lại tính chất của ba đường trung tuyến trong tam giác? (MĐ1).
Câu 2: Bài 23 và bài 24 Sgk/66 (MĐ2, 3).
Tuần: 28 Tiết KHGD: 55 |
Ngày soạn: 15/03/2018 Ngày dạy: 19/03/2018 |
LUYỆN TẬP
I. MỤC TIÊU
1. Kiến thức: Củng cố định lý về tính chất ba đường trung tuyến của một tam giác.
2. Kĩ năng: Luyện kỹ năng sử dụng định lý về tính chất ba đường trung tuyến của một tam giác để giải bài tập. Chứng minh tính chất trung tuyến của tam giác cân, tam giác đều, một dấu hiệu nhận biết tam giác cân.
3. Thái độ: Cẩn thận, chính xác; rèn luyện tư duy, óc quan sát, chứng minh.
4. Xác định nội dung trọng tâm của bài: Củng cố định lý về tính chất ba đường trung tuyến của một tam giác.
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, năng lực hợp tác, năng lực giải quyết vấn đề, năng lực vận dụng, năng lực giao tiếp, năng lực tư duy, năng lực tự quản.
- Năng lực chuyên biệt: Năng lực giải quyết các vấn đề toán học; năng lực tính toán; năng lực sử dụng ngôn ngữ toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ ghi đề bài, thước thẳng, compa, thứơc đo góc.
2. Học sinh: Thước thẳng, compa, thứơc đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Đường trung tuyến của tam giác |
Nhận
biết được đường trung tuyến của
|
|
|
|
2. Tính chất ba đường trung tuyến của tam giác |
|
Hiểu trọng tâm cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó |
Vận dụng được đ/l về sự đồng quy của 3 đường trung tuyến trong 1 tam giác để giải một số bài tập đơn giản. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5')
H: Phát biểu định lý về tính chất ba đường trung tuyến của tam giác.
Á

Hãy
điền và ô trống
![]()
Đáp án: Phát biểu đúng định lý. ....................................4đ
![]() ..................................6đ
..................................6đ
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Tiết học trước các em đã nắm được tính chất của ba đường trung tuyến trong tam giác, tiết học hôm nay các em sẽ luyện tập để củng cố kiến thức cho bài học |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
HOẠT ĐỘNG 2: Luyện tập. (32’) (1) Mục tiêu: Củng cố định lý về tính chất ba đường trung tuyến của một tam giác (2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp. (3) Hình thức tổ chức hoạt động: Toàn lớp (4) Phương tiện dạy học: Bảng phấn, SGK. (5) Sản phẩm: Bài làm của học sinh |
|||
1
Xét vuông ABC, có: BC2 = AB2 + AC2 (đ/lPytago) BC2 = 32 + 42 = 52 BC = 5(cm) AM
=
AG
=
(t/c 3 đường trung tuyến của ) |
Đề bài đưa lên bảng phụ GV yêu cầu HS vẽ hình và ghi GT, KL
GV gọi 1HS lên bảng chứng minh bài toán
GV gọi HS nhận xét |
Một HS đọc to đề bài Một HS lên bảng vẽ hình và ghi GT, KL ABC : Â = 1v GT AB = 3; AC = 4 MB = MC;G là KL Tính AG ?
1HS lên bảng C/m 1 vài HS nhận xét |
Tư duy, giải quyết vấn đề, vận dụng, làm chủ bản thân. |
2
Xét ABE và ACF, có : AB = AC (gt); Â chung AE
= EC =
AF
= FB =
AE = AF Vậy ABE = ACF (c.g.c) BE = CF (cạnh tương ứng)
|
C/m định lý: Trong một cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau GV gọi 1HS lên bảng vẽ hình, ghi GT, KL định lý
H: Để C/m BE = CF ta C/m hai nào bằng nhau? H: Hãy chứng minh ABE = ACF ? GV gọi 1HS chứng minh miệng bài toán, tiếp theo một HS khác lên trình bày bài làm GV yêu cầu HS nêu cách chứng minh khác |
1HS đọc to đề bài 1HS lên bảng vẽ hình và ghi GT, KL ABC, AB = AC GT AE = EC; AF =FB KL BE = CF HS: Để C/m BE = CF ta C/m ABE = ACF hoặc BEC = CFB 1HS chứng minh miệng bài toán 1HS lên bảng trình bày
HS nêu cách c/minh: BEC = CFB BE = CF |
Năng lực tư duy năng lực hợp tác,
|
3. Bài 29.Sgk/67:
Chứng minh
Áp dụng bài 26 ta có: AD = BE = CF Theo định ba đường trung tuyến của ta có: GA
=
GC
=
GA = GB = GC |
GV đưa hình vẽ sẵn và GT, KL lên bảng phụ H: đều là cân ở cả ba đỉnh. Áp dụng bài 26 trên, ta có gì? H: Tại sao GA=GB=GC GVgọi 1HS bảng trình bày. GV gọi HS nhận xét
H: Qua bài 26 và bài 29, em hãy nêu tính chất các đường trung tuyến trong cân, đều |
HS: đọc đề bài và quan sát hình vẽ, GT, KL
Áp dụng bài 26 ta có: AD = BE = CF
1HS lên bảng trình bày cách chứng minh Một vài HS nhận xét HS: Trong cân, trung tuyến ứng với hai cạnh bên thì bằng nhau. Trong đều ba trung tuyến bằng nhau và trọng tâm cách đều ba đỉnh của |
Năng lực tư duy năng lực hợp tác,
|
4. Bài 27.Sgk/67: G AE = EC;BE = CF KL ABC cân
Chứng minhDo BE, CF là hai đường trung tuyến nên ta có: AE = EC, AF = FB (1) G là trọng tâm ABC nên BG = 2EG ; CG = 2FG (2) Do BE = CF nên từ (2) ta có FG = EG, BG = CG BFG = CEG (c.g.c) BF = CE (3) Từ (1) và (3) ta có AB = AC Vậy ABC cân tại A |
GV vẽ hình, yêu cầu HS nêu GT, KL GV gợi ý: Gọi G là trọng tâm . Từ gt BE = CF, em suy ra được điều gì ? H: Vậy tại sao AB=AC?
GV yêu cầu HS làm bài vào vở, gọi 1 HS lên bảng trình bày c/minh GV gọi HS nhận xét GV nhắc nhở HS trình bày các khẳng định phải nêu căn cứ của khẳng định và lưu ý HS : đây là dấu hiệu nhận biết cân |
1HS đọc to đề bài HS: nêu GT, KL HS nghe GV gợi ý và suy nghĩ trả lời
HS ta sẽ chứng minh AGB = GCE (c.g.c) HS cả lớp làm bài vào vở 1HS lên bảng trình bày 1 vài HS nhận xét
HS: nghe GV trình bày |
Năng lực tư duy
|
C. LUYỆN TẬP, CỦNG CỐ: Đã thực hiện ở phần B
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG: 5’
(1) Mục tiêu: Vận dụng tính chất vào giải các bài tập mang tính tư duy
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp, động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng phấn, SGK.
(5) Sản phẩm: Bài làm của học sinh
Bài tập: Cho tam giác ABC, trung tuyến BM, CN cắt nhau tại G, cho biết BM = CN. Chứng minh BN = CM |
Hs: Vì G là trọng tâm tam giác nên BG = (2/3)BM; CG = (2/3) CN Mà BM = CN → BG = CG và NG = MG Ta được ∆ BNG = ∆ CMG ( c.g.c ) → BN = CM |
E. HƯỚNG DẪN VỀ NHÀ: (2’)
Xem lại các bài đã giải.
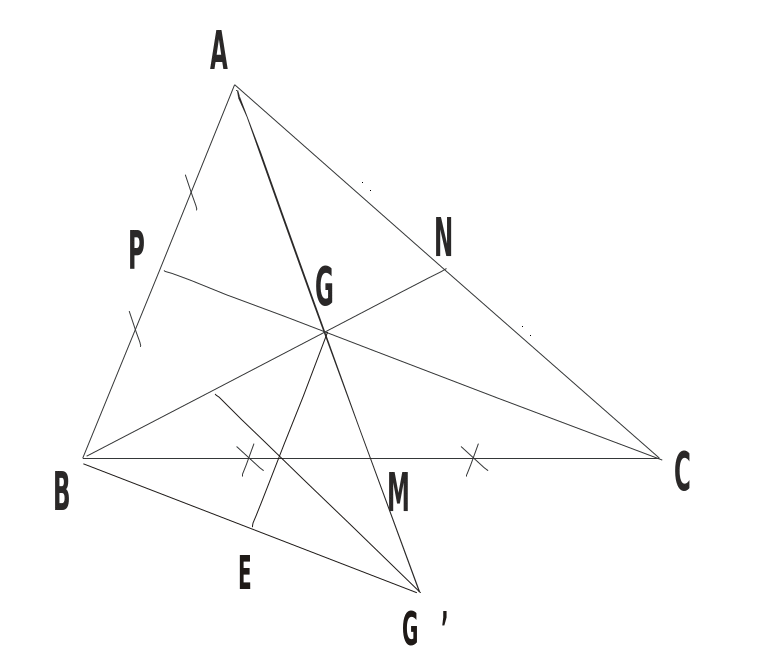
Hướng dẫn bài 30 SGK:
GG’
= GA =
![]() AM
; BG =
AM
; BG =
![]() BN.
BN.
Chứng minh MBG = MCG (c.g.c)
BG’
= CG =
![]() CP
CP
Tuần: 29 Tiết KHGD: 56 |
Ngày soạn: 25/03/2018 Ngày dạy: 26/03/2018 |
|
§5. TÍNH CHẤT TIA PHÂN GIÁC CỦA MỘT GÓC |
|
|
I. MỤC TIÊU:
1. Kiến thức: Học sinh hiểu tính chất các điểm thuộc tia phân giác của một góc và định lý đảo của nó.
2. Kỹ năng: Vận dụng tốt hai định lý vào giải bài tập.
3. Giáo dục: Tính cẩn thận, chính xác, óc tư duy sáng tạo.
4. Nội dung trọng tâm: Nắm được tính chất các điểm thuộc tia phân giác của một góc và định lý đảo của nó
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, giải quyết vấn đề, sáng tạo, tự quản lý, giao tiếp, hợp tác, sử dụng CNTT - TT, sử dụng ngôn ngữ, tính toán.
- Năng lực chuyên biệt: Năng lực tính toán, sử dụng ngôn ngữ toán học, sử dụng các công thức tổng quát, giải quyết các bài toán thực tế và năng lực tư duy lô gic.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: SGK, thước, bảng phụ, êke, thước đo góc.
2. Học sinh: SGK, thước, bảng phụ, êke, thước đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Định lý về tính chất các điểm thuộc tia phân giác |
|
Biết định lý về điểm thuộc tia phân giác của một góc. |
|
|
2. Định lý đảo |
|
|
Chứng minh được điểm thuộc tia phân giác của một góc. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5’)
H: Tia phân gíac của một góc là gì? Cho góc xOy, vẽ tia phân giác Oz của góc đó bằng thước và compa.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV đặt vấn đề: Lấy điểm M thuộc tia p/g của góc xOy, em có nhận xét vị trí điểm M với 2 cạnh của góc xOy? ta sẽ nghiên cứu qua bài học hôm nay. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||
Hoạt động 2: Định lý về tính chất các điểm thuộc tia phân giác. (15’) (1) Mục tiêu: Học sinh hiểu và nắm vững định lý về tính chất của các điểm thuộc tia phân giác của một góc và định lý đảo của nó. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS biết xác định khoảng cách từ điểm M đến đường thẳng a , hiểu thế nào là điểm cách đều 2 đường thẳng. Biết vẽ tia phân giác của một góc bằng thước hai lề. |
|||||
1. Định lí về tính chất các điểm thuộc tia phân giác: a) Thực hành:
b) Định lí (định lí thuận)
GT
MA
KL MA = MB C/m: Xét
OM : chung
Nên
|
GV: yêu cầu HS đọc nội dung thực hành trong SGK. GV: yêu cầu HS thực hành theo SGK để xác định tia phân giác Oz của góc xOy. GV: yêu cầu HS thực hành tiếp theo hình 28 H: với cách gấp như vậy MH là gì?
GV: yêu cầu HS đọc và trả lời.
GV: nêu định lí, yêu cầu HS đọc lại định lí GV:
lấy điểm M bất kì trên OZ, dùng êke vẽ MA
GV: gọi HS chứng minh miệng định lí
GV: chốt lại. GV: Vậy các em đã biết các điểm thuộc tia phân giác của một góc thì cách đều hai cạnh của góc, còn các điểm nằm bên trong góc và cách đều hai cạnh của góc thì có vị trí ntn? |
HS: đọc kĩ nội dung thực hành HS: Thực hành gấp hình theo hình 27 tr 68 SGK HS: thực hành theo hình 28 HS:
Vì MH HS: khi gấp hình các khoảng cáh từ M tới Ox, Oy trùng nhau. Do đó khoảng cách từ M tới Ox, Oy là bằng nhau. HS đọc lại định lí
HS: nêu GT, KL
HS: chứng minh miệng định lí
HS: nhận xét
|
Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
|
||
Hoạt động 3: Định lý đảo. (14’) 1) Mục tiêu: Biết được nội dung định lí đảo cách chứng minh định lí. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kthức, thu thập thông tin, thuyết trình, vấn đáp (3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp (4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập (5) Sản phẩm: Nhận xét về tập hợp các điểm nằm trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó. |
|||||
2
*Định lí 2 (Sgk/69)
?3
G MA MA = MB KL
C/m Xét
MA = MB (gt) OM chung Do
đó
(cạnh huyền – góc nhọn)
|
GV: nêu bài toán SGK tr 69 và vẽ hình 30 lên bảng H: bài toán này cho ta yếu tố nào? Hỏi điều gì ? H: theo em OM có là tia phân giác của góc xOy không? GV: đó là nội dung định lí 2 GV: yêu cầu HS đọc định lí 2 G
?3
GV: yêu cầu HS hoạt nhóm chứng minh
GV: nhận xét
|
HS đọc đề bài toán SGK tr 69 và vẽ hình 30 lên bảng HS:bài toán cho ta M năm trong góc xOy, khoảng cách từ M tới Ox và Oy bằng nhau. HS: OM có là tia phân giác của góc xOy HS: một em đọc định lí 2 HS: nêu GT , KL HS: hoạt động theo nhóm l
HS: đại diện các nhóm lên bảng trình bày
HS: các nhóm nhận xét
|
Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
|
||
C. LUYỆN TẬP, CỦNG CỐ (8’)
(1) Mục tiêu: Củng cố định lý về tính chất của các điểm thuộc tia phân giác của một góc và định lý đảo của nó thông qua giải một số bài tập đơn giản.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài tập 31, 32.
+ Chuyển giao: GV: Yêu cầu HS làm bài tập 31, 32. Sgk/70 trên phiếu học tập, sau đó các nhóm nộp lại kết quả Gv treo lên bảng để cả lớp cùng nhận xét.
|
HS hoạt động nhóm. Sau khoảng 3 - 5 phút đại diện nhóm nộp lại kết quả của nhóm mình. Bài tập 31/70. Khoảng
cách từ M đến Ox và khoảng cách từ M đến Oy đều
là khoảng cách giữa hai lề song song của thước nên
chúng bằng nhau. Do đó theo định lí 2 điểm M nằm
trên tia phân giác của
Bài tập 32/70. GT:
KL:
E thuộc tia phân giác của
Ta
có : EK = EH ( BE là tia phân giác của
EH
= EI (CE là tia phân giác của
Suy ra EK = EI. Vậy
E thuộc tia phân giác của
|
Năng lực tư duy, vận dụng, giao tiếp, làm chủ bản thân, hợp tác. |
D. HƯỚNG DẪN VỀ NHÀ (2’)
Học thuộc định lý ba đường trung tuyến của tam giác.
Bài tập về nhà số: 25; 26; 27 tr 67 SGK. Bài 31; 33 tr 27 SBT. Tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Làm bài tập 31/70.( MĐ2)
Câu 2: Làm bài tập 32/70 sgk(MĐ3)
Tuần: 29 Tiết KHGD: 57 |
Ngày soạn: 26/03/2018 Ngày dạy: 28/03/2018 |
LUYỆN TẬP
I. MỤC TIÊU
1. Kiến thức: Củng cố hai định lý thuận và đảo về tính chất tia phân giác của góc; tập hợp các điểm nằm bên trong góc và cách đều hai cạnh của một góc.
2. Kỹ năng: Rèn kỹ năng phân tích và trình bày bài chứng minh.
3.Giáo dục: Giáo dục tính cẩn thận, óc tư duy sáng tạo.
4. Xác định nội dung trọng tâm của bài: Củng cố định lý về tính chất tia phân giác của góc 5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng có chia khoảng, thước hai lề. Bảng phụ, phấn màu
2. Học sinh: Làm bài tập đã cho, bìa cứng có dạng một góc, bảng nhóm.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Định lý về tính chất các điểm thuộc tia phân giác |
Biết tính chất các điểm thuộc tia phân giác của một góc. |
Hiểu định lý về điểm thuộc tia phân giác của một góc. |
|
|
2. Định lý đảo |
|
|
Chứng minh được điểm thuộc tia phân giác của một góc. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5')
H:
Vẽ
![]() ,
dùng thước hai lề vẽ tia phân giác của
,
dùng thước hai lề vẽ tia phân giác của
![]() .
.
Phát biểu định lí về tính chất các điểm thuộc tia phân giác của một góc?
Đáp án: Vẽ chính xác hình (5đ)
Phát biểu đúng tính chất (5đ)
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Tiết học trước các em đã nắm được hai định lý thuận và đảo về tính chất tia phân giác của góc, tiết học hôm nay các em sẽ luyện tập để củng cố kiến thức cho bài học thông qua việc giải một số bài tập. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
HOẠT ĐỘNG 2: Luyện tập. (32’) (1) Mục tiêu: Củng cố định lý về tính chất tia phân giác của góc (2) Phương pháp/Kĩ thuật dạy học: Tái hiện k.thức, thu thập thông tin, thuyết trình, vấn đáp. (3) Hình thức tổ chức hoạt động: Toàn lớp (4) Phương tiện dạy học: Bảng, phấn, Sgk. (5) Sản phẩm: Bài làm của học sinh |
|||
1
a)
Ta có:
b) Nếu M thuộc đường thẳng Ot thì M O hoặc M Ot, hoặc M tia đối của tia Ot. - Nếu M O thì k /c từ M đến xx’ và yy’ bằng nhau (cùng = 0) - Nếu M Ot thì M cách đều hai tia Ox và Oy, do đó M cách đều hai đường thẳng xx’ và yy’. - Nếu M tia đối của tia Ot thì M cách đều hai tia Ox’ và Oy’, do đó M cách đều hai đường thẳng xx’ và yy’. c) Nếu M cách đều xx’ và yy’ thì M cách đều Ox và Oy, do đó M Ot; hoặc M cách đều Ox, Oy’. Do đó M Ot’ hoặc M cách đều Ox’, Oy’. do đó M tia đối của tia Ot; hoặc M cách đều Ox’, Oy, do đó M tia đối của tia Ot’. Vậy trong mọi trường hợp M luôn thuộc đường thẳng Ot hoặc Ot’. d) Khi M O khoảng cách từ M đến xx’ và yy’ bằng 0. e 2. Bài tập 34/71:
Gt
OA = OC; OB = OD; I = AD BC. K b) IA = IC; IB = ID. c) OI là tia phân giác của góc xOy. Chứng minh: a) Xét AOD và COB có; OA
= OC (gt);
Do đó AOD=COB (c.g.c) Suy ra AD = BC (2 cạnh t/ứ). b) Từ ý a) suy ra:
Vậy AIB = CID (g.c.g) IA = IC; IB = ID. c) OAI = OCI (c.c.c)
Suy ra OI là tia phân giác của góc xOy (đpcm). |
GV: Nêu bài 33 tr 70 SGK GV: Vẽ hình lên bảng, gợi ý và hướng dẫn HS chứng minh. GV: yêu cầu HS chứng minh miệng câu a. GV: ghi lời giải câu a GV: vẽ tia Ox’ là tia đối của tia Ox, vẽ phân giác Os của góc x’Oy’ và phân giác Os’ của góc x’Oy. H: Hãy kể tên các cặp góc kề bù khác trên hình và tính chất các tia phân giác của chúng. H: Vậy Ot và Os là hai tia như thế nào? Tương tự với Ot’ và Os’?
GV: chứng minh miệng câu b. H: Nếu M thuộc đường thẳng Ot thì M có thể ở những vị trí nào? GV: Yêu cầu HS chứng minh cho từng trường hợp.
H: Nhận xét gì về tập hợp các điểm cách đều hai đường thẳng cắt nhau xx’ và yy’? GV: nêu bài 34 tr 71 SGK GV: yêu cầu một HS lên bảng vẽ hình ghi GT, KL
H: để chứng minh BC = AD ta thường quy về chứng minh điều gì? GV: yêu cầu HS khác trình bày miệng câu a GV: gợi ý HS chứng minh câu b bằng cách phân tích đi lên. IA = IC; IB = ID
GV cho HS làm vào vở GV: yêu cầu HS lên bảng trình bày GV cho HS: nhận xét GV: yêu cầu HS phân tích tìm cách chứng minh câu c. GV: nhận xét |
HS làm bài 33 tr 70 SGK HS: Vẽ hình theo hướng dẫn GV.
HS: chứng minh câu a
HS: làm vào vở
HS: vẽ hình vào vở
HS: kể tên các cặp góc kề bù trên hình vẽ.
HS: Tia Ot và Os làm thành một đường thẳng; Ot’ và Os’làm thành một đường thẳng (hoặc hai tia đối nhau)
HS:
M
HS: chứng minh cho từng trường hợp . HS: trình bày chứng minh
HS: nêu nhận xét
HS: lên bảng vẽ hình ghi GT, KL HS: vẽ hình vào vở
HS:
chứng minh
HS: trình bày miệng câu a HS: lần lượt trả lời các câu hỏi gợi ý
HS: làm vào vở HS: một em lên bảng trình bày HS: nhận xét HS: nêu phân tích HS: trình bày chứng minh. HS: nhận xét |
Tư duy, giải quyết vấn đề, vận dụng, tính tốn, giao tiếp, làm chủ bản thân.
Tư duy, giải quyết vấn đề, vận dụng, tính tốn, giao tiếp, làm chủ bản thân.
|
C. LUYỆN TẬP, CỦNG CỐ: Đã thực hiện ở phần B
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG: (5’)
(1) Mục tiêu: Vận dụng định lí vào giải các bài tập mang tính tư duy
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp, động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn, Sgk.
(5) Sản phẩm: HS thấy được mối quan hệ chặt chẽ giữa hai môn Toán học và Vật lí.
+ Chuyển giao nhiệm vụ: Quan sát tìm hiểu về phản xạ ánh sáng: Ta có thí nghiệm sau: Dùng đèn pin chiếu một tia tới lên một gương phẳng. đặt vuông góc với mặt bàn (như hình minh hoạ sau). Tia này đi là là trên mặt bàn, khi gặp gương tia sáng bị hắt lại, cho một tia gọi là tia phản xạ. Hiện tượng này gọi là hiện tượng phản xạ ánh sáng.
- Định luật phản xạ ánh sáng: + Tia phản xạ nằm trong mặt phẳng chứa tia tới và pháp tuyến của gương ở điểm tới. + Góc tới bằng góc phản xạ. (Pháp tuyến của gương chính là đường thẳng vuông góc với mặt gương) Khi đó pháp tuyến chính là tia phân giác của góc tạo bởi tia tới và tia phản xạ.
|
GV mô tả thí nghiệm trên máy chiếu
HS quan sát lắng nghe.
|
E. HƯỚNG DẪN VỀ NHÀ: (2’)
- Nắm vững các định lí về tính chất tia phân giác của góc.
- Xem lại những bài tập đã làm, làm bài tập 35/71. Bài tập 44/29 sbt.
- Mỗi HS chuẩn bị một tam giác bằng giấy cho tiết học sau.
DUYỆT CỦA CHUYÊN MÔN DUYỆT CỦA TỔ
Chư Prông, ngày.......tháng.......năm 2018 Chư Prông, ngày.......tháng.......năm 2018
Tuần: 30 Tiết KHGD: 58 |
Ngày soạn: 31/03/2018 Ngày dạy: 02/04/2018 |
|
§6. TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC |
|
|
I. MỤC TIÊU:
1. Kiến thức: HS hiểu khái niệm đường phân giác của tam giác và biết mỗi tam giác có ba đường phân giác. HS tự chứng minh được định lý: “Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến ứng với cạnh đáy”.
2. Kĩ năng: Rèn luyện kỹ năng gấp hình, suy luận, chứng minh, áp dụng định lý vào bài tập.
3. Thái độ: Rèn luyện ý thức tự giác, tự rèn luyện.
4. Xác định nội dung trọng tâm của bài: Nắm được tính chất ba đường phân giác của tam giác.
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, năng lực hợp tác, năng lực giải quyết vấn đề, năng lực vận dụng, năng lực giao tiếp, năng lực tư duy, năng lực tự quản lý (năng lực làm chủ bản thân).
- Năng lực chuyên biệt: Năng lực giải quyết các vấn đề toán học; năng lực tính toán; năng lực sử dụng ngôn ngữ toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Một tam giác bằng bìa mỏng gấp hình, thước hai lề, ê ke, compa.
2. Học sinh: Mỗi em có một tam giác bằng giấy, thước thẳng, compa, thước đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Đường phân giác của tam giác.
|
Nhận biết được đường phân giác của tam giác.
|
Biết vẽ ba đường phân giác của tam giác. |
|
|
2. Tính chất ba đường phân giác của tam giác. |
|
|
Vận dụng được tính chất ba đường phân giác của tam giác. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (10’)
HS1: Xét xem các mệnh đề sau đúng hay sai?
1) Bất kỳ điểm nào thuộc tia phân giác của một góc cũng cách đều hai cạnh của góc đó. (Đúng)
2) Bất kỳ điểm nào cách đều hai cạnh của một góc cũng nằm trên tia phân giác của góc đó.
(Sai, bổ sung nằm bên trong góc đó)
3) Hai đường phân giác hai góc ngoài của một tam giác và đường phân giác của góc thứ ba cùng đi qua một điểm. (Đúng)
4) Hai tia phân giác của hai góc bù nhau thì vuông góc với nhau.
Sai: (sửa lại) Hai tia phân giác của hai góc kề bù thì vuông góc với nhau)
H

![]() cắt BC tại M.
cắt BC tại M.
Chứng minh MB = MC.
 GT
ABC
GT
ABC
AB = AC; Â1 = Â2
 KL
MB = MC
KL
MB = MC
Chứng minh:
Xét AMB và AMC,có: AB = AC (gt), Â1 = Â2; AM chung
Nên AMB = AMC (c.g.c) MB = MC
GV gọi HS nhận xét cho điểm.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
Từ bài tập phần KTBC GV đặt vấn đề: Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đối diện với đáy có tính chất gì đặc biệt ta sẽ nghiên cứu qua bài học hôm nay. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||
HOẠT ĐỘNG 2: Đường phân giác của tam giác. (8’) (1) Mục tiêu: Học sinh biết được khái niệm đường phân giác của một tam giác và tính chất của đường phân giác trong tam giác cân. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS biết cách vẽ đường phân giác của tam giác |
|||||
1. Đường phân giác của tam giác
AM là đường phân giác xuất phát từ đình A của ABC
Mỗi có ba đường phân giác
Tính chất: Sgk |
GV Vẽ ABC, vẽ tia phân giác của  cắt Cạnh BC tại M và giới thiệu đoạn AM là đường phân giác (xuất phát từ đỉnh A) của ABC. GV Trở lại bài tập (bài cũ). Hãy cho biết trong cân đường phân giác xuất phát từ đỉnh đồng thời là đường gì của tam giác? Yêu cầu HS đọc tính chất của cân Sgk H: Một có mấy đường phân giác? H: Ba đường phân giác của có tính chất gì ? |
H
HS Trả lời: Đường phân giác AM đồng thời là đường trung tuyến của HS: Đọc to tính chất này. HS: Có ba đường phân giác HS trả lời:
|
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân.
|
||
HOẠT ĐỘNG 3: Tính chất ba đường phân giác của . (15’) (1) Mục tiêu: Häc sinh n¾m v÷ng tính chất ba đường phân giác của tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS chứng minh được và n¾m v÷ng tính chất ba đường phân giác của tam giác. - Biết cách xác định điểm cách đều 3 cạnh của tam giác. - Biết thêm cách khác để chứng minh tia phân giác của một góc. |
|||||
2. Tính chất ba đường phân giác của tam giác: Định lý: Sgk/72
Chứng minh: Sgk |
Bài ?1 Có nhận xét gì về ba nếp gấp này ? Tính chất ba đường phân giác GV vẽ ABC, 2 đường phân giác xuất phát từ B, C cắt nhau tại I. Ta sẽ chứng minh AI là phân giác của  và I cách đều 3 cạnh của ABC. Yêu cầu HS làm bài ?2 Hãy chứng minh bài toán? Hướng dẫn: I
? I CF ? |
HS: thực hiện ?1 Cùng đi qua một điểm
HS: đọc định lý Sgk/72
HS: chứng minh trình bày tương tự Sgk/72 |
Tư duy, giải quyết vấn đề, giao tiếp làm chủ bản thân |
||
C. LUYỆN TẬP, CỦNG CỐ (10’)
(1) Mục tiêu: Häc sinh củng cố kh¸i niÖm ®êng ph©n gi¸c cña tam gi¸c vµ n¾m v÷ng tính chất ba đường phân giác của tam giác
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài tập 36, 38.
+ Chuyển giao: GV: Yêu cầu HS phát biểu tính chất 3 đường phân giác của ? Làm bài tập 36, 38. Sgk/72, 73 *Bài 36 Sgk/72 Chứng minh: Có I nằm trong DEF nên I nằm trong DÊF. Có IP = IH (gt) I thuộc tia phân giác của DÊF. Tương
tự I cũng thuộc tia phân giác của
*Bài 38 Sgk/73
a) Xét IKL có:
Có
Xét OKL
= 1800 590 = 1210 b)
Vì O là giao điểm hai đường phân giác xuất phát từ
K và L nên IO là phân giác của
c) Theo chứng minh trên có O là điểm chung của ba đường phân giác của nên O cách đều 3 cạnh của . |
Giải bài tập 36 Sgk/72
Yêu cầu HS chứng minh miệng bài tập
GV treo đề trên bảng phụ
Yêu cầu HS hoạt động nhóm câu a, b a) Tính KÔL b)
Kẻ tia IO. Hãy tính
GV nhận xét và kiểm tra bài làm của vài nhóm.
Điểm O có cách đều 3 cạnh của IKL không ? Tại sao?
|
HS: phát biểu định lý
HS: viết GT, KL HS: Có I nằm trong DEF nên I nằm trong DÊF. Có IP = IH (gt) I thuộc tia phân giác của DÊF. Tương
tự I cũng thuộc tia phân giác của
Hoạt động nhóm làm bài.
|
Năng lực vận dụng
Năng lực hợp tác, giao tiếp. |
D. HƯỚNG DẪN VỀ NHÀ (1’)
- Học thuộc bài. Nắm được tính chất 3 đường phân giác của tam giác.
- Làm bài tập 37, 39, 40 Sgk/73. Tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Hãy phát biểu tính chất ba đường phân giác của tam giác? (MĐ 1).
Câu 2: Bài 36 và bài 38 Sgk (MĐ 2, 3)
Tuần: 30 Tiết KHGD: 59 |
Ngày soạn: 31/03/2018 Ngày dạy: 04/04/2018 |
LUYỆN TẬP
I. MỤC TIÊU
1. Kiến thức: Củng cố các định lý về tính chất ba đường phân giác của , tính chất đường phân giác của một góc ngoài, tính chất đường phân giác của tam giác cân, tam giác đều
2. Kĩ năng: Rèn luyện kỹ năng vẽ hình, phân tích và chứng minh bài toán. Chứng minh một dấu hiệu nhận biết tam giác cân.
3. Thái độ: Học sinh thấy được ứng dụng thực tế của tính chất ba đường phân giác của tam giác, của một góc.
4. Xác định nội dung trọng tâm của bài: Củng cố định lý về tính chất ba đường phân giác của tam giác
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, năng lực hợp tác, năng lực giải quyết vấn đề, năng lực vận dụng, năng lực giao tiếp, năng lực tư duy, năng lực tự quản lý.
- Năng lực chuyên biệt: Năng lực giải quyết các vấn đề toán học; năng lực tính toán; năng lực sử dụng ngôn ngữ toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Sgk, bảng phụ, thước thẳng, compa, êke, thước hai lề.
2. Học sinh: Thực hiện hướng dẫn tiết trước, thước thẳng, compa, thứơc đo góc, Ôn tập các định lý về tính chất về tia phân giác của 1 góc, tính chất ba đường phân giác của , tính chất cân, đều.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Đường phân giác của tam giác, Tính chất ba đường phân giác của tam giác |
|
Hiểu tính chất ba đường phân giác của tam giác đồng quy tại một điểm, điểm đó cách đều ba cạnh của tam giác. |
Vận dụng được đ/l về sự đồng quy của ba đường phân giác trong một tam giác để giải một số bài tập đơn giản.
|
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (7')
HS: Phát biểu tính chất ba đường phân giác của tam giác? Chữa bài tập 37 Sgk/72
Đáp án: Phát biểu đúng tính chất ...................4đ
HS Vẽ hình. Trong 1 ba đường phân giác cùng đi qua 1 điểm nên MK là phân giác của góc M. Điểm K cách đều 3 cạnh của theo tính chất 3 đường phân giác của ...................6đ
GV gọi HS nhận xét cho điểm.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Tiết học trước các em đã nắm được định lý về tính chất ba đường phân giác của tam giác, tiết học hôm nay các em sẽ luyện tập để củng cố kiến thức cho bài học thông qua việc giải một số bài tập. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
HOẠT ĐỘNG 2: Luyện tập. (35’) (1) Mục tiêu: Củng cố khái niệm và tính chất 3 đường phân giác của tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện k.thức, thu thập thông tin, thuyết trình, vấn đáp. (3) Hình thức tổ chức hoạt động: Toàn lớp (4) Phương tiện dạy học: Bảng, phấn, Sgk. (5)
Sản phẩm: Lời
giải các bài tập; HS nắm được các cách vẽ tia phân
giác của 1 góc bằng đo
độ, com pa, thước
2 lề. Các cách chứng minh tia phân giác của 1 góc (c/m
2
|
|||
1. Bài 39. Sgk/73 G Â1 = Â2 K b)
Chứng minh: a)
Xét
AB = AC (gt); Â1 = Â2 (gt); AD chung nên
b)
Vì
=> BD = CD (2 cạnh t/ứng) Nên
=> |
Gv: Yêu cầu Hs làm bài tập 39. Sgk/73 (Treo bảng phụ có hình vẽ) H: Bài toán cho biết gì và y/cầu điều gì? Hd:
có AB = AC; Â1= Â2; AD chung H:
Để c/m
BD = CD
|
Hs: Đọc đề bài 39. Sgk
Một HS nêu GT, KL
1HS lên bảng C/m theo hướng dẫn.
1 vài HS nhận xét |
Tư duy, giải quyết vấn đề, vận dụng, làm chủ bản thân. |
2. Bài 40 Sgk/73 GT G Là trọng tâm I là giao điểm của 3 đường phân giác KL A; G; I thẳng hàng
M Chứng minh: Vì ABC cân tại A nên phân giác AM của đồng thời là trung tuyến (t/c cân) G là trọng tâm của nên G AM. I là giao điểm của các đường phân giác của nên I AM A, G, I thẳng hàng vì cùng thuộc AM |
Gv: Yêu cầu Hs đọc đề bài 40. Sgk Nêu yêu cầu đề? H:
Trọng tâm của tam giác là gì ? làm thế nào để xác
định được trọng tâm của
Còn I được xác định như thế nào ? Yêu cầu cả lớp vẽ hình ghi GT, KL H: ABC cân tại A vậy phân giác AM của đồng thời là đường gì ? H: Tại sao G, I, A thẳng hàng ? GV gọi HS nhận xét GV hoàn chỉnh và sửa sai nếu có |
1HS đọc to đề bài
HS Trả lời: Vẽ hai trung tuyến của , giao điểm của chúng là trọng tâm G. Ta vẽ hai tia phân giác, giao của chúng là I, cả lớp vẽ hình ghi GT, KL vào vở HS: đứng tại chỗ trả lời
HS Trả lời
Một vài HS nhận xét |
Năng lực tự học, năng lực tư duy năng lực hợp tác |
3
Xét ADB và A’DC có: AD = A’D (cách vẽ)
DB = DC (gt) Nên ADB = A’DC Â1 = Â2 và AB = A’C Xét CAA’ có Â2 = Â’= Â1 CAA’ cân AC = A’C (đ/n cân) mà A’C = AB (cmt) AC = AB Vậy ABC cân tại A |
Bài 42: C/minh định lý Nếu có một đường trung tuyến đồng thời là tia phân giác thì là cân. GV hướng dẫn HS vẽ hình, kéo dài AD một đoạn DA’ = AD. Gợi ý phân tích bài toán ABC cân AB = AC có AB = A’C AC = A’C (ADB = A’DC) CAA’ cân Â’ = Â2 H: Em nào có cách chứng minh khác GV có thể hướng dẫn
|
HS: đọc đề bài, vẽ hình viết GT, KL
GT ABC, Â1 = Â2 BD = DC KL ABC cân
HS: có thể đưa ra cách chứng minh khác. |
Năng lực tư duy năng lực hợp tác
|
C. LUYỆN TẬP, CỦNG CỐ: Đã thực hiện ở phần B
D. HƯỚNG DẪN VỀ NHÀ: (2’)
- Học ôn các tính chất đường phân giác của góc, tính chất và dấu hiệu nhận biết cân.
- Định nghĩa đường trung trực của đoạn thẳng.
- Làm bài tập: 49; 50; 51; 52/29 sbt.
- Chuẩn bị một mảnh giấy có một mép thẳng cho bài học sau.
Tuần: 31 Tiết KHGD: 60 |
Ngày soạn: 08/04/2018 Ngày dạy: 09/04/2018 |
§7. TÍNH CHẤT ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG
I. MỤC TIÊU:
1. Kiến thức: Biết tính chất đường trung trực của một đoạn thẳng.
2. Kĩ năng: HS biết cách vẽ đường trung trực của một đoạn thẳng, xác định được trung điểm của một đoạn thẳng bằng thước kẻ và compa.
3. Thái độ: Bước đầu biết dùng các định lí này để làm các bài tập đơn giản.
4. Xác định nội dung trọng tâm của bài: Biết tính chất đường trung trực của một đoạn thẳng và định lí đảo của nó. Nắm vững được nội dung và cách chứng minh hai định lí. Biết tóm tắt GT, KL định lý; tóm tắt GT, KL bài toán.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ, phấn màu, thước thẳng, compa, êke.
2. Học sinh: Thước thẳng, compa, êke, bảng nhóm.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Tính chất đường trung trực của một đoạn thẳng.
|
Biết tính chất các điểm thuộc đường trung trực của một đoạn thẳng. |
Hiểu cách c/m định lí thuận và định lí đảo |
Biết vận dụng tính chất các điểm thuộc đường trung trực của một đoạn thẳng để ứng dụng vào bài cụ thể. |
Vận dụng tính chất để chứng minh
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5’)
H: Thế nào là đường trung trực của một đoạn thẳng? (5 điểm)
T rả
lời:
Đường trung trực của một đoạn thẳng là đường
thẳng vuông góc với đoạn thẳng tại trung điểm của
đoạn thẳng đó.
rả
lời:
Đường trung trực của một đoạn thẳng là đường
thẳng vuông góc với đoạn thẳng tại trung điểm của
đoạn thẳng đó.
Bài tập: Cho đoạn thẳng AB, hãy vẽ đường trung trực của đoạn thẳng AB. M
Lấy M thuộc d. So sánh MA = MB. (5 điểm)
GV gọi HS nhận xét cho điểm.
A. KHỞI ĐỘNG d
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Chúng ta vừa ôn lại khái niệm đường trung trực của một đoạn thẳng, cách vẽ đường trung trực của đoạn thẳng bằng thước có chia khoảng và êke. Nếu dùng thước thẳng và compa có thể dựng được đường trung trực của một đoạn thẳng hay không? Chúng ta sẽ nghiên cứu qua bài học hôm nay. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||
HOẠT ĐỘNG 2: Định lí về tính chất các điểm thuộc đường trung trực. (10’) (1) Mục tiêu: HS biết tính chất điểm thuộc trung trực của đoạn thẳng. Biết cách giải bài tập liên quan đến kiến thức đã học ở mức độ nhận biết. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS rút ra được định lý thuận và biết vẽ hình minh họa. |
|||||
1. Định lí về tính chất các điểm thuộc đường trung trực:
M I
C
D E
A
K B
A I
C
D E
A
K B
A I
C
D E
A
K B
B I
C
D E
A
K B
// I
C
D E
A
K B
// I
C
D E
A
K B
I I
C
D E
A
K B
d I
C
D E
A
K B
GT M thuộc trung trực của đoạn thẳng AB KL MA = MB |
GV: lấy một mảnh giấy trong đó có một mép cắt là đoạn AB. GV: yêu cầu HS thực hành gấp hình theo hướng dẫn của Sgk (hình 41a, b) H: Tại sao nếp gấp 1 chính là đường trung trực của đoạn thẳng AB? GV: Yêu cầu HS thực hành tiếp (hình 41 c), độ dài nếp gấp 2 là gì ? H: Hai khảng cách này như thế nào ? H: Vậy điểm nằm trên trung trực của một đoạn thẳng có tính chất gì? GV: Nhấn mạnh nội dung định lí. Sau đó yêu cầu HS vẽ hình và c/minh định lí. |
HS: thực hành gấp hình theo Sgk (hình 41a, b)
HS: Vì nếp gấp đó vuông góc với AB tại trung điểm của nó.
HS: thực hành gấp hình theo SGK (hính 41c) HS: Khoảng cách từ M tới hai điểm A và B. HS: Nêu định lí
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp làm chủ bản thân.
|
||
HOẠT ĐỘNG 3: Định lí đảo. (10’) (1) Mục tiêu: HS biết được khi nào một điểm nằm trên đường trung trực của một đoạn thẳng. Biết cách giải bài tập liên quan đến kiến thức đã học ở mức độ nhận biết. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS rút ra được định lý đảo |
|||||
2. Định lí đảo:
a
A
M
B
b)
?1 GT Đoạn thẳng AB, MA = MB
KL M thuộc trung trực của đoạn thẳng AB Chứng minh: (Sgk)
|
H: Hãy lập mệnh đề đảo của định lí trên? GV: Vẽ hình và yêu cầu HS thực hiện ?1 GV: yêu cầu HS nêu cách chứng minh (xét hai trường hợp)
GV:
Trường hợp b có thể nêu cách chứng minh khác: Từ M
hạ MI
GV: Nêu lại định lí thuận và đảo rồi đi tới nhận xét. |
HS: Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. HS: Thực hiện ?1
HS: Có thể chứng minh như Sgk
HS: Đọc lại nhận xét tr 75 Sgk |
Năng lực tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân.
|
||
HOẠT ĐỘNG 4: Ứng dụng. (8’) (1) Mục tiêu: HS biết cách vẽ đường trung trực của một đoạn thẳng, xác định được trung điểm của một đoạn thẳng bằng thước kẻ và compa. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS biết thêm cách vẽ đường trung trực của một đoạn thẳng bằng thước kẻ và compa. |
|||||
P R
M I N
Q R
>
+
PM = PN = R
QM
= QN = R
|
GV: Dựa vào tính chất trên, ta có thể vẽ được đường trung trực của một đoạn thẳng bằng thước và compa. GV: vẽ đoạn thẳng MN và đường trung trực. GV: nêu chú ý Sgk/76 GV: yêu cầu HS chứng minh PQ là đường trung trực của đoạn thẳng MN. GV: Gợi ý cho HS bằng cách nối PM, PN, QM, QN. |
HS: vẽ hình theo hướng dẫn của GV
HS: chứng minh GV: Gợi ý cho HS bằng cách nối PM, PN, QM, QN.
|
Tư duy, giải quyết vấn đề, vận dụng, tính tốn, giao tiếp, làm chủ bản thân.
|
||
C. LUYỆN TẬP, CỦNG CỐ (9’)
(1) Mục tiêu: Củng cố định lý về tính chất của các điểm thuộc đường trung trực và cách vẽ đường trung trực của một đoạn thẳng bằng thước kẻ và compa.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải bài tập 44.
+ Chuyển giao: GV Yêu cầu HS làm bài tập 44, 46 tr76 Sgk. GV: yêu cầu HS dùng thước thẳng và com pa vẽ đường trung trực của đoạn thẳng AB. GV: Nhận xét
|
H
- Bài tập 44/76 sgk. vì M thuộc đường trung trực của đoạn thẳng AB nên MA = MB = 5cm
- Bài tập 46/76 sgk.( MĐ 2,3, 4) GT:
Kl : A, D, E thẳng hàng
Ta có: AB
= AC
DB
= DC
EB
= FE
Vậy ba điểm A, D, E thẳng hàng. |
Năng lực tư duy, vận dụng, giao tiếp, làm chủ bản thân, hợp tác. |
D. HƯỚNG DẪN VỀ NHÀ (2’)
- Học thuộc các 2 định lí về tính chất đường trung trực của đoạn thẳng, vẽ thành thạo đường trung trực của một đoạn thẳng bằng thước vàcompa.
- Ôn lại khi nào hai điểm A và B đối xứng nhau qua đthẳng xy.
- Làm bài tập 45, 47, 48, 51.Sgk
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Nêu tính chất các điểm thuộc đường trung trực của 1 đoạn thẳng? Làm bài 44. (MĐ1)
Câu 2: Làm bài tập 46 Sgk/76. (MĐ 2, 3, 4)
Tuần: 31 Tiết KHGD: 61 |
Ngày soạn: 08/04/2018 Ngày dạy: 11/04/2018 |
LUYỆN TẬP
I. MỤC TIÊU
1. Kiến thức: Củng cố các địmh lí về tính chất đường trung trực của một đoạn thẳng.
2. Kĩ năng:
+ Biết vận dụng các định lí đó vào việc giải các bài tập hình (chứng minh, dựng hình)
+ Rèn luyện kĩ năng vẽ đường trung trực của một đoạn thẳng cho trước, dựng đường thẳng qua một điểm cho trước bằng thước thẳng và com pa.
3. Thái độ: Giải bài toán thức tế có ứng dụng tính chất đường trung trực của một đoạn thẳng
4. Xác định nội dung trọng tâm của bài: Biết tính chất đường trung trực của một đoạn thẳng và định lí đảo của nó. Nắm vững được nội dung và cách chứng minh hai định lí. Biết tóm tắt GT, KL định lý; tóm tắt GT, KL bài toán.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Thước thẳng, compa, bảng phụ, phấn màu
2. Học sinh: Thực hiện hướng dẫn tiết trước.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Tính chất đường trung trực của một đoạn thẳng.
|
Biết tính chất các điểm thuộc đường trung trực của một đoạn thẳng. |
Hiểu cách c/m định lí thuận và định lí đảo |
Biết vận dụng tính chất các điểm thuộc đường trung trực của một đoạn thẳng để ứng dụng vào bài cụ thể. Biết tóm tắt định lý; tóm tắt GT, KL bài toán. |
Vận dụng tính chất để chứng minh.
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (7’)
H: Nêu định lí thuận và đảo về tinh chất đường trung trực của một đoạn thẳng? (6 điểm)
Làm bài tập 47.Sgk/76 (4 điểm)
Đ áp
án:
Điểm nằm trên đường trung trực của một đoạn thẳng
thì cách đều hai mút của đoạn thẳng đó. Ngược lại,
điểm cách đều hai mút của đoạn thẳng thì nằm trên
đường trung trực của một đoạn thẳng đó.
................6đ
áp
án:
Điểm nằm trên đường trung trực của một đoạn thẳng
thì cách đều hai mút của đoạn thẳng đó. Ngược lại,
điểm cách đều hai mút của đoạn thẳng thì nằm trên
đường trung trực của một đoạn thẳng đó.
................6đ
Làm bài tập 47.Sgk/76 ...............4đ
Vì M, N nằm trên đường trung trực của đoạn AB nên.
MA = MB (1)
và NA = NB (2)
Suy
ra
![]() AMN
=
AMN
=
![]() BMN
(c.c.c)
BMN
(c.c.c)
GV gọi HS nhận xét cho điểm.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Tiết học trước các em đã nắm được định lý về tính chất các điểm thuộc đường trung trực, tiết học hôm nay các em sẽ luyện tập để củng cố kiến thức cho bài học thông qua việc giải một số bài tập thực tế. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
HOẠT ĐỘNG 2: Luyện tập. (35’) (1) Mục tiêu: Củng cố các địmh lí về tính chất đường trung trực của một đoạn thẳng. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện k.thức, thu thập thông tin, thuyết trình, vấn đáp. (3) Hình thức tổ chức hoạt động: Toàn lớp (4) Phương tiện dạy học: Bảng, phấn, Sgk, compa, êke và thước thẳng. (5) Sản phẩm: Vận dụng các định lí về tính chất đường trung trực của một đoạn thẳng vào việc giải các bài tập hình (chứng minh, dựng hình). |
|||
1. Bài 49.Sgk/77:
C
A’
Lấy A’ đối xứng với A qua bờ sông. Giao của A’B với bờ sông là C, nơi xây dựng trạm bơm. 2. Bài 50.Sgk/77: Địa điểm xây dựng trạm y tế là giao của đường trung trực nối hai điểm dân cư với cạnh đường quốc lộ.
3. Bài 48.Sgk/77:
Mx
N
y
x
P
I
L Ta có: IM = IL Nếu
I
Hay IM + IN > LN Nếu
I
IL + IN = PL + PN = LN 4. Bài 51.Sgk/77: a
d A B
C b) Chứng minh: Theo cách dựng PA = PB; CA = CB.
Vậy
PC là trung trực của đoạn thẳng AB
C
d A B
Q |
GV: Nêu bài 49 Sgk/77 GV: Vẽ hình lên bảng H: Bài toán này tương tự bài toán nào ?
GV: Yêu cầu HS trình bày lời giải
GV: Nêu bài 50 Sgk/77 H: Địa điểm nào xây dựng trạm y tế cách đều hai điểm dân cư?
GV: Nêu bài 48 Sgk/77 GV: Vẽ hình lên bảng H: Nêu cách vẽ điểm L đối xứng với M qua xy?
GV: Gợi ý IM bằng đoạn nào ? Tại sao?
H: IM + IN nhỏ nhất khi nào?
GV: Nêu bài 51 Sgk/77 GV: Yêu cầu HS hoạt động theo nhóm.
GV: Yêu cầu các nhóm trình bày lời giải. GV: Kiểm tra kết quả của vài nhóm. H: còn cách dựng nào khác không? (bằng thước và compa) GV: Tiến hành dựng cho HS xem GV: yêu cầu HS nêu lại cách dựng GV: Nhận xét |
HS: Nêu bài 49 Sgk/77 HS: Vẽ hình vào vở HS: Tương tự bài 48 Sgk vừa chữa
HS: Trình bày lời giải
HS: Đọc bài 50 Sgk/77 HS: Trả lời
HS khác : Nhận xét
HS: Vẽ hình vào vở HS: xy là trung trực của đoạn ML.
HS: IM = IL vì I nằm trên trung trực của đoạn ML.
HS:
IM + IN nhỏ nhất khi I
HS: Đọc bài 51 Sgk/77 HS: Hoạt động theo nhóm thực hiện theo hai nội dung: dựng hình và chứng minh.
HS:Đại diện các nhóm trình bày lời giải
HS: suy nghĩ trả lời
HS: Quan sát cách dựng của GV
HS: nêu cách dựng HS: Nhận xét
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
|
|||
C. LUYỆN TẬP, CỦNG CỐ: Đã thực hiện ở phần B
D. HƯỚNG DẪN VỀ NHÀ: (2’)
- Ôn tập các định lí về tính chất các đường trung trực của một đoạn thẳng, các tính chất của tam giác cân đã biết. Luyện thành thạo cách dựng đường trung trực của một đoạn thẳng bằng thước và compa.
- Làm bài tập về nhà 57, 59 tr 30, 31 SBT.
Tuần: 32 Tiết KHGD: 62 |
Ngày soạn: 15/04/2018 Ngày dạy: 16/04/2018 |
|
§8. TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC |
|
|
I. MỤC TIÊU:
1. Kiến thức: Biết khái niệm đường trung trực của một tam giác, chỉ rõ mỗi tam giác có ba đường trung trực.
2. Kĩ năng: Biết cách dùng thước kẻ và compa vẽ ba đường trung trực của tam giác.
Chứng minh được định lí “trong tam giác cân đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh đáy”. Chứng minh được định lí 2. Biết khái niệm đường tròn ngoại tiếp tam giác.
3. Thái độ: Biết vận dụng hai định lí trên để giải bài tập. Có ý thức trình bày lời giải rõ ràng, lập luận có căn cứ.
4. Xác định nội dung trọng tâm của bài: Nắm được tính chất ba đường đường trung trực của một tam giác.
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, hợp tác, giải quyết vấn đề, vận dụng, giao tiếp, tư duy, năng lực tự quản lý (năng lực làm chủ bản thân).
- Năng lực chuyên biệt: Năng lực giải quyết các vấn đề toán học; năng lực tính toán; năng lực sử dụng ngôn ngữ toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Sgk, bảng phụ, thước thẳng, compa, êke, thước hai lề.
2. Học sinh: Thực hiện hướng dẫn tiết trước, thước thẳng, compa, thứơc đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Đường trng trực của tam giác |
Nhận biết được đường trung trực của tam giác. Biết vẽ 3 đường trung trực của tam giác |
|
|
|
2. Tính chất ba đường trung trực của tam giác |
Biết ba đường trung trực của tam giác đồng quy tại một điểm, điểm đó cách đều ba đỉnh của tam giác. |
Hiểu chứng minh sự đồng quy của ba đường trung trực |
Vận dụng tính chất ba đường trung trực của tam giác |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (6’)
HS1: Cho ABC dùng thước và compa dựng 3 đường trung trực của
c

Đáp án:
HS vẽ hình, ba đường trung trực của ba cạnh ABC cùng đi qua một điểm.......10đ
HS2: Cho cân DEF (DE = DF). Vẽ đường trung trực của cạnh đáy EF.
Chứng minh đường trung trực này đi qua đỉnh D của .
Giải: Có DE = DF (gt) D cách đều E và F nên d phải thuộc trung trực của EF
hay trung trực EF đi qua D. ...........................10đ
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Ở tiết học trước ta được ôn lại đường trung trực của một đoạn thẳng và tính chất của nó. Vậy đường trung trực của tam giác được xác định như thế nào và có tính chất gì đặc biệt? Chúng ta sẽ nghiên cứu qua bài học hôm nay. |
HS lắng nghe
|
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
|||
HOẠT ĐỘNG 2: Đường trung trực của tam giác. (10’) (1) Mục tiêu: HS biết khái niệm đường trung trực của tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS vễ được đường trung trực của tam giác. |
||||||
1. Đường trung trực của tam giác.
a là đường trung trực của tam giác ABC. Mỗi tam giác có ba đường trung trực.
*Trong một tam giác cân đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.
|
GV đưa hình lên bảng phụ và hỏi: Vậy một tam giác có mấy đường trung trực? H: Trong một tam giác bất kỳ đường trung trực của một cạnh có nhất thiết đi qua đỉnh đối diện với cạnh ấy hay không ? Trường hợp nào đường trung trực của một tam giác đi qua đỉnh đối diện với cạnh ấy H: Đoạn thẳng DI nối đỉnh của tam giác với trung điểm của cạnh đối diện. Vậy DI là đường gì của DEF? (Phần KTBC) GV từ c/minh trên ta có tính chất GV nhấn mạnh: trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là trung trực của cạnh đáy, cũng đồng thời là đường trung tuyến của tam giác. |
HS: có 3 đường trung trực
HS: Trả lời
HS: Đoạn thẳng DI là đường trung tuyến của DEF |
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp làm chủ bản thân.
|
|||
HOẠT ĐỘNG 3: Tính chất ba đường trung trực của tam giác. (16’) (1) Mục tiêu: HS biết tính chất ba đường trung trực của tam giác. Biết xác định giao ba đường trung trực của một tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: Rút ra tính chất ba đường trung trực của tam giác, giao của ba đường trung trực của tam giác gọi là điểm cách đều 3 đỉnh của tam giác. |
||||||
2. Tính chất ba đường trung trực của tam giác: Định lý: Sgk/78 ABC, b, c là GT trung trực của AC AB, b cắt c tại O KL O nằm trên đường Trung trực của BC OA = OB = OC Chứng minh: Sgk
|
GV yêu cầu HS đọc định lý Sgk/78 H: Hãy nêu GT, KL của định lý? GV: Để c/m định lý này ta cần dựa trên 2 định lý thuận và định lý đảo của đoạn thẳng GV g.thiệu đường tròn ngoại tiếp tam giác ABC là đường tròn đi qua ba đỉnh của tam giác. H
|
HS: đọc định lý HS: nêu GT, KL
Ta chỉ cần vẽ hai đường trung trực của tam giác, giao điểm của chúng sẽ là tâm của đường tròn ngoại tiếp tam giác vì đường trung trực thứ ba cũng đi qua giao điểm ABC nhọn O nằm bên trong tam giác ABC vuông O nằm trên cạnh huyền ABC tù O nằm bên ngoài tam giác |
Tư duy, giải quyết vấn đề, giao tiếp làm chủ bản thân
Năng lực vận dụng
|
|||
C. LUYỆN TẬP, CỦNG CỐ (10’)
(1) Mục tiêu: Củng cố về tính chất ba đường trung trực của tam giác. Vận dụng lý thuyết giải bài tập.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải bài tập 52, 53.Sgk/79; bài 64. SBT/31
Bài 64 tr 31 SBT Điểm O cách đều 3 đỉnh của ABC là giao điểm của ba đường trung trực của tam giác. Bài 53 tr 80 SGK: Coi 3 ngơi nhà là 3 đỉnh của tam giác. Vị trí chọn đào giếng là giao điểm các đường trung trực của tam giác đó, có ba đỉnh là vị trí của ba ngôi nhà. Bài 52 tr 79 SGK: Giải: Có AM vừa là cạnh huyền, vừa là trung trực ứng với cạnh BC của ABC AB = AC ABC cân tại A |
Bài 64 SBT: Cho ABC. Tìm một đường tròn cách đều ba đỉnh A, B, C
Bài 53 tr 80 SGK: (Bảng phụ)
Bài 52 tr 79 SGK: (Bảng phụ)
|
HS Trả lời: Điểm O cách đều 3 đỉnh của ABC là giao điểm của ba đường trung trực của tam giác H
|
Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, tự học.
|
D. HƯỚNG DẪN VỀ NHÀ (2’)
Ôn tập các định lý về tính chất đường trung trực của một đoạn thẳng, tính chất ba đường trung trực của tam giác, cách vẽ trung trực.
Bài tập về nhà: 54; 55 Sgk/80; 65; 66 tr 31 SBT
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Phát biểu định lí về tính chất đường trung trực của tam giác cân ?( MĐ1)
Câu 2: Bài tập 52, 53/80 sgk; bài 64 Sbt: ( MĐ 2, 3)
Tuần: 32 Tiết KHGD: 63 |
Ngày soạn: 15/04/2018 Ngày dạy: 18/04/2018 |
|
LUYỆN TẬP |
|
|
I. MỤC TIÊU:
1. Kiến thức: Củng cố các định lý về tính chất đường trung trực của một đoạn thẳng. Tính chất ba đường trung trực của tam giác, một số tính chất của tam giác cân, tam giác vuông
2. Kĩ năng: Rèn luyện kỹ năng vẽ đường trung trực của tam giác, vẽ đường tròn ngoại tiếp tam giác, chứng minh ba điểm thẳng hàng và tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông.
3. Thái độ: HS thấy được ứng dụng thực tế của tính chất đường trung trực của đoạn thẳng
4. Xác định nội dung trọng tâm của bài: Củng cố các định lý về tính chất đường trung trực của một đoạn thẳng. Tính chất ba đường trung trực của tam giác.
5. Định hướng phát triển năng lực:
- Năng lực chung: Năng lực tự học, năng lực hợp tác, năng lực giải quyết vấn đề, năng lực vận dụng, năng lực giao tiếp, năng lực tư duy, năng lực tự quản lý (năng lực làm chủ bản thân).
- Năng lực chuyên biệt: Năng lực giải quyết các vấn đề toán học; năng lực tính toán; năng lực sử dụng ngôn ngữ toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Sgk, thước thẳng, compa, êke.
2. Học sinh: Thước thẳng, compa, thước đo góc.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Đường trung trực của tam giác. Tính chất ba đường trung trực của tam giác . |
Biết chứng minh sự đồng quy của ba đường trung trực.
|
Chứng minh được 3 đường trung trực của một tam giác đồng quy tại một điểm. Điểm đó là tâm đường tròn ngoại tiếp tam giác. |
Vận dụng được đ/l về sự đồng quy của 3 đường trung trực trong 1 tam giác để giải một số bài tập đơn giản. |
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (10’)
HS1: Phát biểu tính chất của ba đường trung trực của tam giác? Vẽ đường tròn đi qua ba đỉnh của tam giác vuông ABC (Â = 1v). Nêu nhận xét về vị trí tâm O của đường tròn ngoại tiếp tam giác vuông?
HS2: Thế nào là đường tròn ngoại tiếp tam giác, cách xác định tâm của đường tròn này. Hãy xác định vị trí của tâm đường tròn ngoại tiếp các tam giác tù, nhọn, vuông?
Trả lời: HS phát biểu Sgk
Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
Tâm của đường tròn ngoại tiếp tam giác tù nằm ngoài tam giác.
Tâm của đường tròn ngoại tiếp tam giác nằm bên trong tam giác.
GV gọi HS nhận xét, cho điểm.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Tiết học trước các em đã nắm được định lý về tính chất ba đường trung trực của tam giác, tiết học hôm nay các em sẽ luyện tập để củng cố kiến thức cho bài học thông qua việc giải một số bài tập thực tế. |
HS lắng nghe
|
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||
HOẠT ĐỘNG 2: Luyện tập. (32’) (1) Mục tiêu: Củng cố các địmh lí về tính chất đường trung trực của một đoạn thẳng, tính chất ba đường trung trực của tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện k.thức, thu thập thông tin, thuyết trình, vấn đáp. (3) Hình thức tổ chức hoạt động: Toàn lớp (4) Phương tiện dạy học: Bảng, phấn, Sgk, compa, êke và thước thẳng. (5) Sản phẩm: Học sinh hiểu và vận dụng lý thuyết để giải các bài tập |
|||||
1. Bài tập 1: Cho
hình vẽ bên. C/m AD Chứng minh điểm A, D thuộc trung trực của đoạn thẳng BC Suy ra AD là trung trực của đoạn thẳng BC Suy
ra AD
2. Bài 55 Sgk/80
Chứng minh: Có D thuộc đường T2 của AB
Nên
Tương
tự có
*Nhận
xét:
Ta có
3. Bài 57 Sgk/80
- Lấy 3 điểm A, B, C phân biệt trên cung tròn - Vẽ đường trung trực của AB, BC. Giao của 2 đường trung trực này là tâm đường tròn bị gãy (điểm O) - Bán kính của đường viền là khoảng cách từ O đến 1 điểm bất kỳ của cung tròn (= OA) 4. Bài tập Cho
|
GV phát phiếu học tập cho HS
GV chốt kiến thức, chốt điểm
GV yêu cầu học sinh làm bài tập 55
H: Hãy đọc hình vẽ? (H.vẽ cho biết điều gì?) Ghi GT-KL của bài toán? H: Để chứng minh B, D, C thẳng hàng ta làm ntn ?
- Hãy tính góc BDA theo Â1 ? - Tương tự, hãy tính góc ADC theo Â2 ?
- Từ đó, hãy tính góc BDC ?
- Có n.xét gì về điểm D? - Vậy điểm cách đều 3 đỉnh của tam giác vuông là điểm? - Độ dài đường trung tuyến xuất phát từ đỉnh góc vuông q.hệ như thế nào với độ dài cạnh huyền ? GV nhấn mạnh tính chất đường trung tuyến trong tam giác vuông và tính chất trung điểm của cạnh huyền. GV yêu cầu học sinh làm tiếp bài tập 57 (SGK) (H.vẽ đưa lên bảng phụ) H: Làm thế nào để xđ được bán kính của đường viền này?
GV yêu cầu học sinh đọc đề bài, vẽ hình, ghi GT, KL GV hướng dẫn HS phân tích bài toán tìm hướng giải
|
HS thảo luận nhóm
Đại diện nhóm trình bày
Các nhóm nhận xét đánh giá lẫn nhau
HS: đọc hình viết GT, KL
HS:
C/m
........................ Học sinh trình bày lời giải của bài tập HS rút ra nhận xét về điểm D HS: Điểm cách đều 3 đỉnh của tam giác vuông là TĐ của cạnh huyền HS: Học sinh nghe giảng và ghi bài
Học sinh đọc đề bài và làm bài tập 57
HS: Bước 1: Xác định tâm của đường tròn bị gãy Bước 2: Xác định khoảng cách từ tâm đến 1 điểm trên đường viền
HS đọc đề bài, vẽ hình, ghi GT, KL
Cá nhân HS phát biểu từng ý
HS về nhà hoàn thiện bài. |
Năng lực tự học, làm chủ bản thân.
Năng lực tư duy năng lực hợp tác, vận dụng
|
||
C. LUYỆN TẬP, CỦNG CỐ: Đã thực hiện ở phần B
D. HƯỚNG DẪN VỀ NHÀ: (2’)
- Học bài, vận dụng được tính chất ba đường trung trực của tam giác.
- Làm bài tập 64, 68/31 sbt. Xem trước “Tính chất ba đường cao của tam giác”.
Tuần: 33 Tiết KHGD: 64 |
Ngày soạn: 20/04/2018 Ngày dạy: 23/04/2018 |
|
§9. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC |
|
|
I. MỤC TIÊU:
1. Kiến thức: HS biết khái niệm đường cao của tam giác và mỗi tam giác có ba đường cao.
2. Kĩ năng: Luyện cách dùng êke để vẽ đường cao của tam giác. Qua vẽ hình nhận biết ba đường cao của tam giác luôn đi qua một điểm. Từ đó vận dụng định lí về tính chất đồng quy của ba đường cao của tam giác để giải bài tập.
3. Thái độ: Rèn tư duy, suy luận hợp lí.
4. Xác định nội dung trọng tâm của bài: Biết khái niệm đường cao của tam giác và tính chất ba đường cao tam giác. Nắm vững được nội dung và cách chứng minh hai định lí. Biết tóm tắt GT, KL định lý; của bài toán.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phụ, phấn màu, compa, êke, thước kẻ.
2. Học sinh: Làm bài tập đã cho, bảng nhóm, compa, êke, thước kẻ.
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Đường cao của tam giác. Tính chất ba đường cao của tam giác. |
Biết vẽ đường cao của một tam giác. |
Thông qua hình vẽ biết tính chất ba đường cao của một tam giác. |
|
Vận dụng tính chất để ứng dụng vào bài cụ thể. Biết tóm tắt bài toán. |
2. Về các đường cao, trung tuyến, trung trực, phân giác của tam giác cân |
Biết vẽ đường cao, trung tuyến, trung trực, phân giác ứng với cạnh đáy của một tam giác cân. |
Hiểu tính chất về đường cao, trung tuyến, trung trực, phân giác của một tam giác cân. |
Biết vận dụng tính chất để ứng dụng vào bài cụ thể. Biết tóm tắt GT, KL bài toán.
|
|
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5’)
H: Qua một điểm nằm ngoài một đường thẳng vẽ được mấy đường vuông góc với đường thẳng đó?
Cho điểm A nằm ngoài đường thẳng a hãy dùng êke để vẽ đường thẳng đi qua A và vuông góc với a.
Đ áp
án:
Qua 1 điểm nằm ngoài một đường thẳng vẽ được một
đường vuông góc với đường thẳng đó. (5đ)
áp
án:
Qua 1 điểm nằm ngoài một đường thẳng vẽ được một
đường vuông góc với đường thẳng đó. (5đ)
(5đ)
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Ở các tiết học trước ta đã biết trong một tam giác 3 đường trung tuyến, 3 đường phân giác, 3 đường trung trực đều gặp nhau tại một điểm. Hôm nay, chúng ta học tiếp một đường chủ yếu nữa của tam giác thông qua §9. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||||
HOẠT ĐỘNG 2: Đường cao của tam giác. (5’) (1) Mục tiêu: HS biết khái niệm đường cao của tam giác và mỗi tam giác có ba đường cao. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS nắm được khái niệm và xác định được số đường cao của tam giác. |
|||||||
1
B I C AI: đường cao của tam giác ABC |
GV: Vẽ tam giác ABC lên bảng GV: Vẽ đoạn vuông góc từ đỉnh đến cạnh đối diện và giới thiệu đó là đường cao. H: Một tam giác có mấy đường cao? GV: Y/c HS lên bảng vẽ 2đường cao còn lại của tam giác ABC. |
HS: vẽ hình vào vở và nghe GV trình bày. HS: một tam giác có ba đường cao. HS: Lên bảng vẽ hình. |
Tư duy, vẽ hình, giao tiếp, làm chủ bản thân. |
||||
HOẠT ĐỘNG 3: Tính chất ba đường cao của tam giác. (10’) (1) Mục tiêu: HS biết được tính chất ba đường cao của tam giác. HS nhớ tên gọi giao điểm và biết cách xác định giao ba đường cao của tam giác (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS nhớ được nhận xét về ba đường cao của một tam giác và biết được tính chất ba đường cao của tam giác cùng đi qua một điểm. |
|||||||
2
B
C
I K L A
I
B
C *Ba đường cao của tam giác cùng đi qua một điểm. |
GV: Yêu cầu HS thực hiện ?1 GV: chia lớp làm 3 phần: 1/3 lớp vẽ tam giác nhọn; 1/3 lớp vẽ tam giác tù; 1/3 lớp vẽ tam giác vuông. GV: Gọi 3 HS lên bảng vẽ hình. GV cho HS nêu nhận xét
GV: giới thiệu định lí về tính chất ba đường cao. |
HS: thực hiện ?1
HS: ba em lên bảng vẽ hình HS: nêu nhận xét
HS nghe GV giới thiệu định lí về tính chất ba đường cao. |
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, làm chủ bản thân. |
||||
HOẠT ĐỘNG 4: Về các đường cao, trung tuyến, trung trực, p/g của tam giác cân (14’) (1) Mục tiêu: HS biết được tính chất về các đường đồng quy trong tam giác cân, biết thêm được DHNB tam giác cân. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp. (4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập (5) Sản phẩm: HS thấy được tính chất về các đường đồng quy trong tam giác cân và biết thêm DHNB tam giác cân. |
|||||||
3. Về các đường cao, trung tuyến, trung trực, phân giác của tam giác cân: A
B I C
*Tính chất của tam giác cân Sgk/82
*Nhận xét: Sgk/82
|
GV: Cho tam giác cân ABC (AB = AC). Vẽ trung trực của đáy BC. H: Tại sao đường trung trực của BC lại đi qua A?
H: Vậy đường trung trực của BC đồng thời là đường gì của tam giác cân ABC? H: AI còn là đường gì của tam giác ? GV: Vậy ta có tính chất sau của tam giác cân. GV: Đưa “Tính chất tam giác cân lên bảng phụ” GV: Đảo lại một tam giác có các đường như thế nào là tam giác cân? GV: Nêu Nhận xét. Yêu cầu HS đọc lại nhận xét. GV: Y/c HS thực hiện ?2 H: Áp dung tính chất trên vào tam giác đều ta có điều gì? |
HS: Vẽ hình vào vở.
HS: Vì AB = AC (theo tính chất trung trực của một đoạn thẳng). HS:
AI
HS: AI còn là phân giác của góc A, vì trong tam giác cân, đường trung tuyến ứng với cạnh đáy đồng thời là phân giác của góc ở đỉnh. HS: Hai em lần lượt nêu lại tính chất.
HS đọc lại nhận xét.
HS: thực hiện ?2 HS: Nêu tính chất cho tam giác đều. |
Tư duy, giải quyết vấn đề, vận dụng, vẽ hình, giao tiếp, làm chủ bản thân. |
||||
C. LUYỆN TẬP, CỦNG CỐ (8’)
(1) Mục tiêu: HS hiểu và vận dụng lý thuyết giải các bài tập.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải bài tập 58.
H: Nêu tính chất ba đường cao của một tam giác? H: Nêu tính chất tính chất về đường cao, trung tuyến, trung trực, phân giác của một tam giác cân. + Chuyển giao: GV Yêu cầu HS làm bài tập 58 tr83 Sgk.
GV: Nhận xét
|
HS: Trả lời
HS hoạt động nhóm làm bài. -
Trong
- Trong tam giác tù, hai đường cao xuất phát từ hai đỉnh góc nhọn nằm bên ngoài tam giác nên trực tâm của tam giác tù nằm bên ngoài tam giác. |
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, tự học. |
D. HƯỚNG DẪN VỀ NHÀ (2’)
- Học thuộc các định lí, tính chất, nhận xét trong bài.
- Ôn lại định nghĩa, tính chất các đường đồng quy trong tam giác, phân biệt bốn loại đường.
-
?2
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Nêu tính chất ba đường cao của một tam giác.. (MĐ 1)
Câu 2: Nêu tính chất tính chất về đường cao, trung tuyến, trung trực, phân giác của một tam giác cân. (MĐ 2)
Câu 3: Bài tập 58/83 sgk (MĐ 3, 4)
Tuần: 33 Tiết KHGD: 65 |
Ngày soạn: 20/04/2018 Ngày dạy: 24/04/2018 |
|
LUYỆN TẬP |
|
|
I. MỤC TIÊU:
1. Kiến thức: Phân biệt các loại đường đồng quy trong một tam giác. Củng cố tính chất về đường cao, trung tuyến, trung trực, phân giác của tam giác cân.
2. Kĩ năng: Rèn luyện kĩ năng xác định trực tam của tam giác, kĩ năng vẽ hình theo đề bài, phân tích và chứng minh bài tập hình.
3. Thái độ: Rèn tư duy, suy luận hợp lí.
4. Xác định nội dung trọng tâm của bài: Củng cố kiến thức về đường đồng quy của tam giác cân. Vận dụng các tính chất này để giải bài tập. Biết tóm tắt GT, KL bài toán.
5. Định hướng phát triển năng lực:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân, hoạt động nhóm.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên: Bảng phu, thước thẳng, compa, êke, phấn màu.
2. Học sinh: Bảng nhóm, thước thẳng, compa, êke
3. Bảng tham chiếu các mức yêu cầu cần đạt của câu hỏi, bài tập, kiểm tra, đánh giá.
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
1. Đường cao của một tam giác. Tính chất ba đường cao của một tam giác. |
Biết vẽ đường cao của một tam giác. |
|
Biết vận dụng tính chất vào bài cụ thể. Biết tóm tắt GT, KL bài toán. |
|
2. Về các đường cao, trung tuyến, trung trực, phân giác của tam giác cân |
|
Biết vẽ đường cao, trung tuyến, trung trực, phân giác ứng với cạnh đáy của tam giác cân. |
|
Biết vận dụng tính chất để ứng dụng vào bài cụ thể. |
III. HOẠT ĐỘNG DẠY- HỌC:
* Kiểm tra bài cũ: (5’)
H: Phát biểu tính chất về ba đường cao của tam giác? Tính chất của cân? đều?
*Đáp án: Ba đường cao của một tam giác cùng đi qua một điểm. Điểm này gọi là trực tâm của tam giác. (2đ)
Tính chất: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó (4đ)
Trong tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau. (4đ)
GV gọi HS nhận xét, cho điểm.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
Hoạt động của GV |
Hoạt động của HS |
GV: Tiết học trước các em đã nắm được tính chất ba đường cao của tam giác, tính chất về các đường đồng quy trong tam giác cân và biết thêm DHNB tam giác cân. Tiết học hôm nay, chúng ta sẽ luyện tập để củng cố kiến thức cho bài học thông qua việc giải một số bài tập thực tế. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||
HOẠT ĐỘNG 2: Luyện tập. (32’) (1) Mục tiêu: Củng cố kiến thức về đường đồng quy của tam giác cân. Vận dụng các tính chất này để giải bài tập. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện k.thức, thu thập thông tin, thuyết trình, vấn đáp. (3) Hình thức tổ chức hoạt động: Toàn lớp (4) Phương tiện dạy học: Bảng, phấn, Sgk, compa, êke và thước thẳng. (5) Sản phẩm: HS hiểu và vận dụng lý thuyết giải các bài tập dạng: Chứng minh tam giác cân, biết các cách chứng minh một tam giác cân. Chứng minh hai đường thẳng vuông góc. Tính số đo góc. Trình bày nói và viết thành thạo. |
|||||
1 Giải G AH
Chứng minh: Xét
Nên
AB = AC (cạnh tương ứng) Vậy
2. Bài tập 59/83 sgk.
a)
Trong
b)
Trong
= 900 - 500 = 400 Trong
= 900 - 40 0 = 500
+
Ta có
= 1300 3. Bài tập 61/83 sgk:
a)
Vậy
A là trực tâm của
b)
Tương tự trực tâm của
4. Bài 62 Sgk/83:
GT
BM = CN C/m Xét
MC = BN (gt)
=>
=>AC = AB (2 cạnh tương ứng) =>
chứng minh tương tự ta có:
=> CB = CA (2) Từ
(1), (2) =>
|
GV: Nêu bài tập (ghi ở bảng phụ) GV yêu cầu 1HS lên bảng vẽ hình và tóm tắt GT, KL
GV yêu cầu 1HS nêu cách chứng minh GV gọi 1HS trình bày lại bài làm ở trên bảng.
GV: Gọi một HS đọc đề bài tập 59/83 sgk.
GV vẽ hình 57sgk lên bảng.
H: bài toán cho biết gì và yêu cầu gì ? -
Vì sao NS
-
-
-
-
GV: Gọi một HS đọc đề bài tập 61/83 sgk. H:
Hãy chỉ ra các đường cao của
-
Trực tâm của
-
Trực tâm của
GV: Nêu bài tập (ghi ở bảng phụ)
GV cho HS đọc đề bài
GV yêu cầu 1HS nêu cách chứng minh
GV gọi 1HS trình bày lại bài làm ở trên bảng.
|
HS: đọc đề bài 1HS lên bảng vẽ hình và tóm tắt GT, KL
1HS nêu cách chứng minh 1 HS lên bảng trình bày bài HS ghi bài
HS: đọc đề bài
HS quan sát vẽ hình vào vở
HS: trả lời
HS: Một HS lên bảng làm, HS còn lại làm và nhận xét. HS: Hoạt động nhóm làm câu b, đại diện trình bày.
HS: Lên bảng vẽ hình.
HS: Hoạt động nhóm lần lượt trả lời từng câu hỏi.
HS: đọc đề bài 1HS lên bảng vẽ hình và tóm tắt GT, KL
1HS nêu cách chứng minh
1 HS lên bảng trình bày bài HS ghi bài |
Tư duy, giải quyết vấn đề, vận dụng, làm chủ bản thân.
Tư duy, giải quyết vấn đề, vận dụng, hoạt động nhóm, làm chủ bản thân. |
||
C. LUYỆN TẬP, CỦNG CỐ: Đã thực hiện ở mục B
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG: (5’)
(1) Mục tiêu: HS hiểu và vận dụng lý thuyết giải bài tập mang tính tư duy
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp, động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn, Sgk.
(5) Sản phẩm: Lời giải bài toán.
H: Nêu tính chất ba đường cao của một tam giác? H: Nêu tính chất tính chất về đường cao, trung tuyến, trung trực, phân giác của một tam giác cân. + Chuyển giao nhiệm vụ: GV Yêu cầu HS làm bài tập: Cho tam giác ABC vuông tại A. Đường phân giác của góc B cắt AC tại H . Kẻ HE vuông góc với BC ( (E € BC) . Đường thẳng EH và BA cắt nhau tại I . a) Chứng minh ΔABH = ΔEBH b) Chứng minh BH là trung trực của AE. So sánh HA và HC c) Chứng minh BH vuông góc với IC. Có nhận xét gì về tam giác IBC? |
HS: Trả lời
HS hoạt động nhóm theo hướng dẫn của giáo viên. Về nhà hoàn thành lời giải |
Tư duy, giải quyết vấn đề, vận dụng, giao tiếp, tự học. |
E. HƯỚNG DẪN VỀ NHÀ (2’)
- Học thuộc các định lí, tính chất, nhận xét trong bài.
- Ôn lại định nghĩa, tính chất các đường đồng quy trong tam giác, phân biệt bốn loại đường.
- Xem và làm lại các bài tập đã giải
- Chuẩn bị các câu hỏi và bài tập ôn tập chương III để tiết sau ôn tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Câu 1: Nêu tính chất ba đường cao của một tam giác. (MĐ1)
Câu 2: Nêu tính chất tính chất về đường cao, trung tuyến, trung trực, phân giác của tam giác cân.(MĐ2)
Câu 3: Làm bài tập (MĐ3, 4)
Ngoài Giáo Án Hình Học 7 Phương Pháp Mới 5 Hoạt Động Học Kì 2 thì các tài liệu học tập trong chương trình 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm







 .
.

 .
.

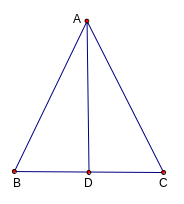 )
)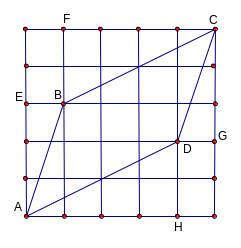 )
) :
Em nào có thể chứng minh được hai tam giác ADB và ADC
bằng nhau?
:
Em nào có thể chứng minh được hai tam giác ADB và ADC
bằng nhau?


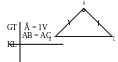
 V
cho hình vẽ,
V
cho hình vẽ,
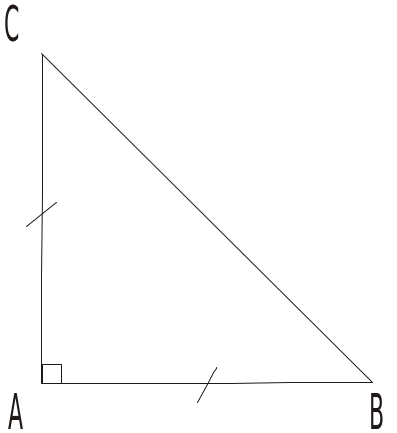

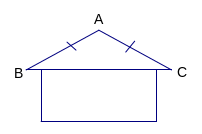 .
.
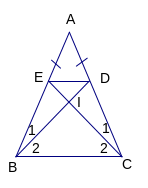
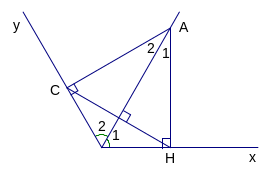
 1
1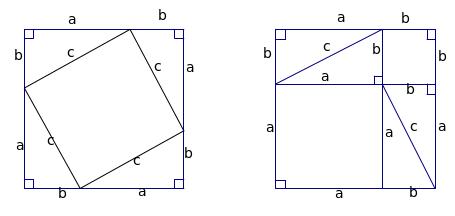
 ịnh
lí đảo
ịnh
lí đảo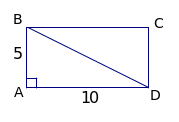 .
.
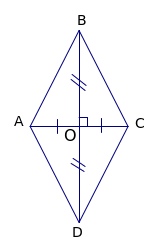 .
.
 .
.
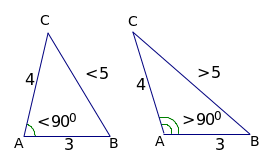 S
trả lời
S
trả lời
 )
)


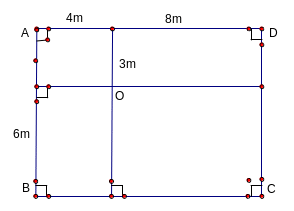
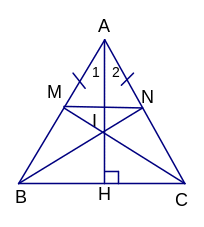

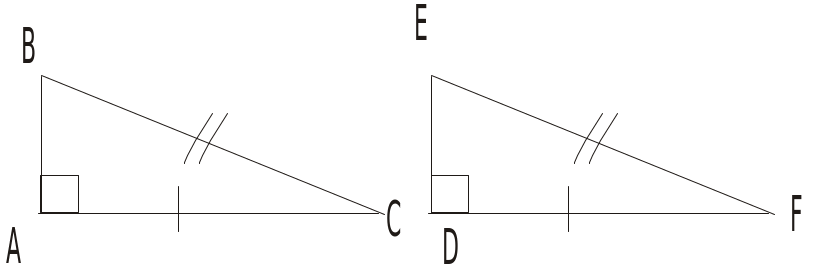

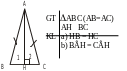 Bài
63.Sgk/136
Bài
63.Sgk/136


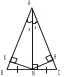 )
)
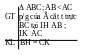

 Bước 5: Hãy chứng tỏ AB = CD.
Bước 5: Hãy chứng tỏ AB = CD.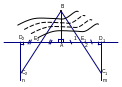 V:
Sơ đồ bố trí hai tổ thực hành:
V:
Sơ đồ bố trí hai tổ thực hành: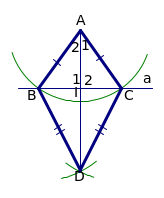 .
Bài 3 (Bài 69.Sgk/141)
.
Bài 3 (Bài 69.Sgk/141) .
Bài 4 (Bài 108.SBT/111)
.
Bài 4 (Bài 108.SBT/111)
 A
= OC (gt)
A
= OC (gt)


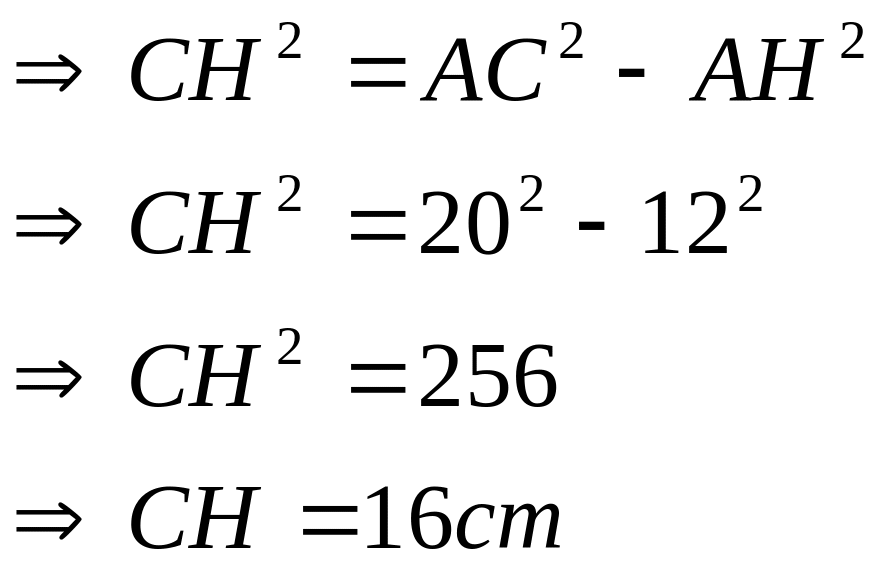


 T
T

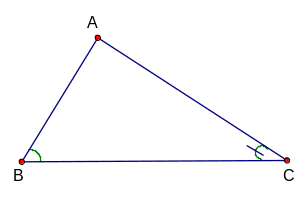
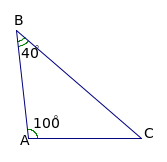 )
) )
)
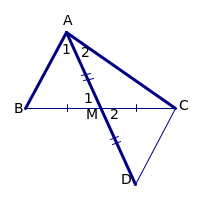 )
)
 T
T
 .
.
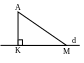 S:
Lên bảng trình bày
S:
Lên bảng trình bày

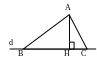 4:
4:
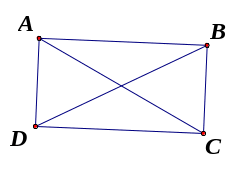

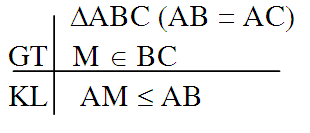
 )
)
 t
t
 l
a) BE < BC
l
a) BE < BC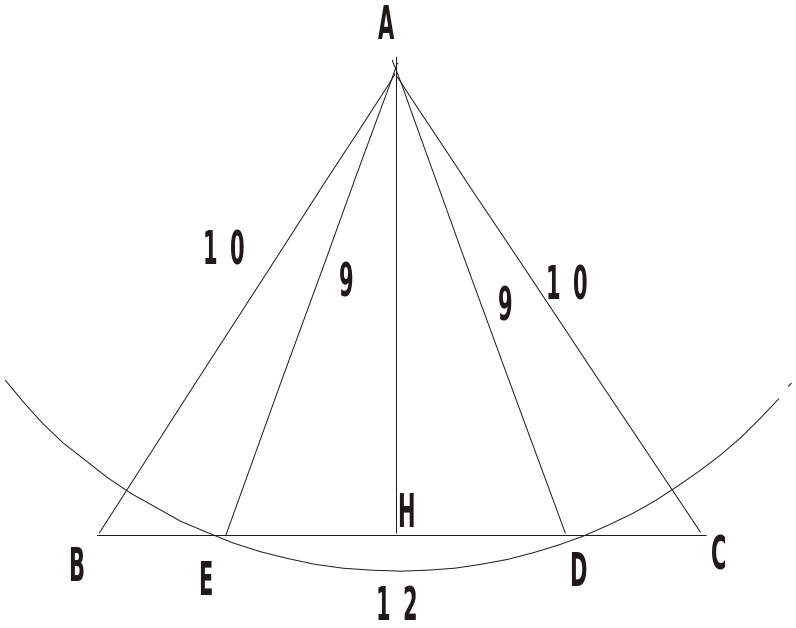
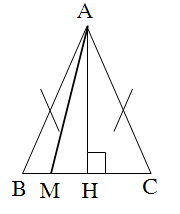


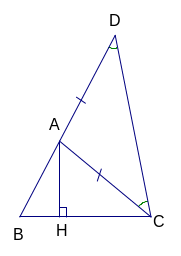


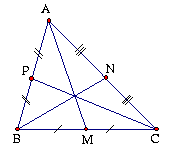
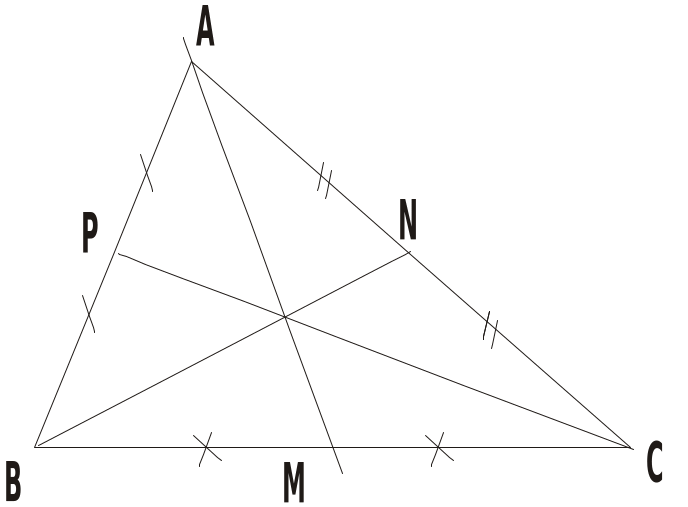

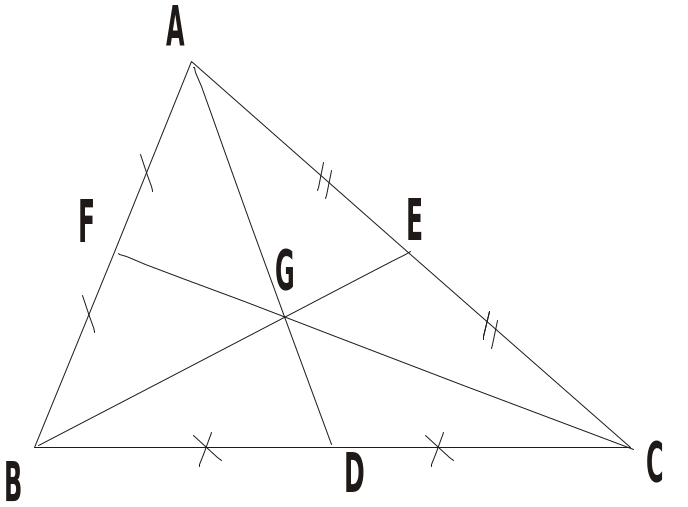
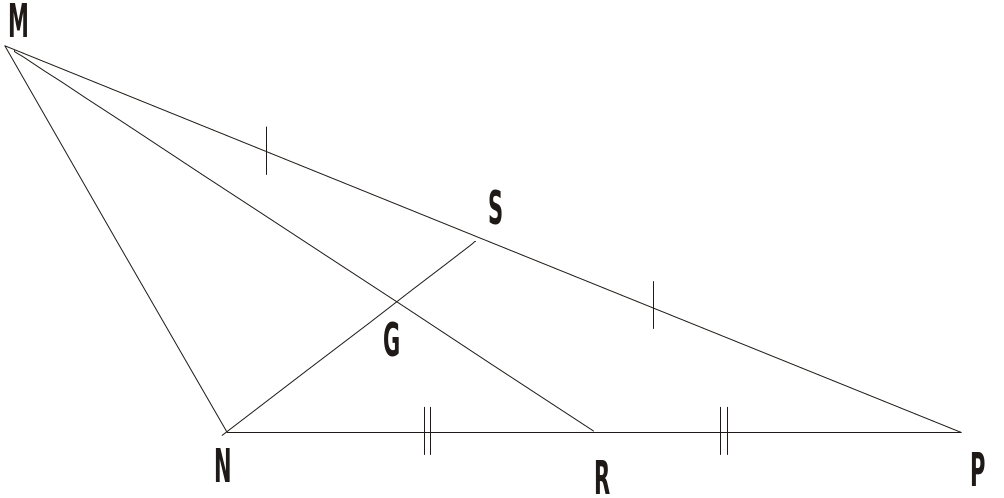


 T
T 
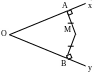 .
.

 T
M nằm trong góc xOy
T
M nằm trong góc xOy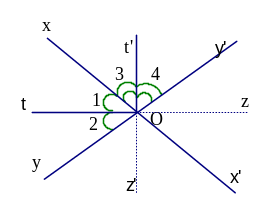 .
.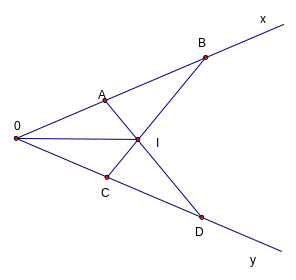 )
Tập hợp các điểm cách đều hai đường thẳng cắt
nhau xx’ và yy’ là hai đường phân giác Ot và Ot’
của hai cặp góc đối đỉnh được tạo thành từ xx’
và yy’.
)
Tập hợp các điểm cách đều hai đường thẳng cắt
nhau xx’ và yy’ là hai đường phân giác Ot và Ot’
của hai cặp góc đối đỉnh được tạo thành từ xx’
và yy’.
 l
a) BC = AD.
l
a) BC = AD.



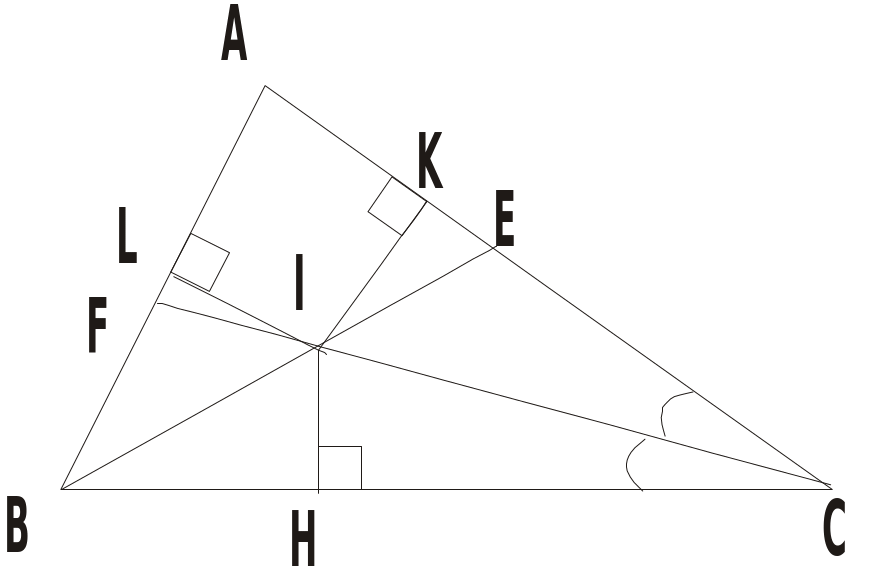
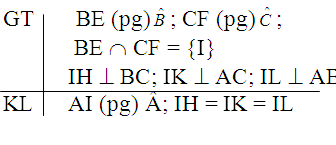


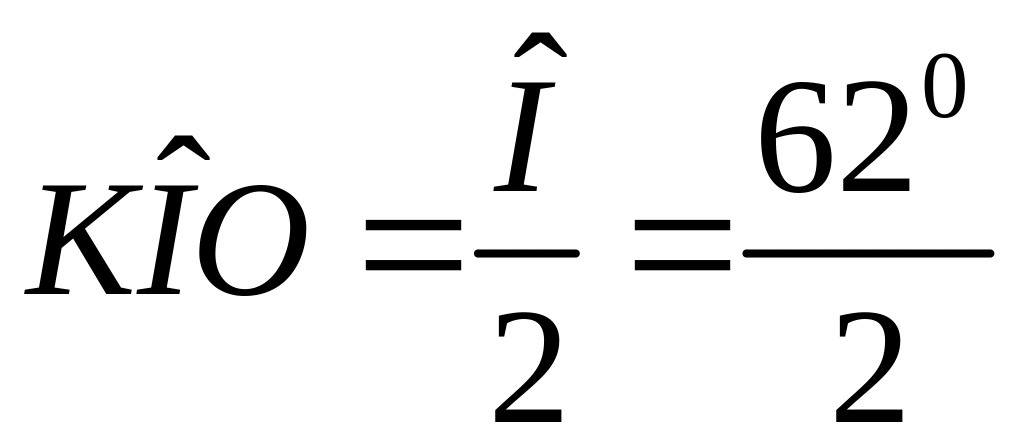

 t
t
 L
a)
L
a) 

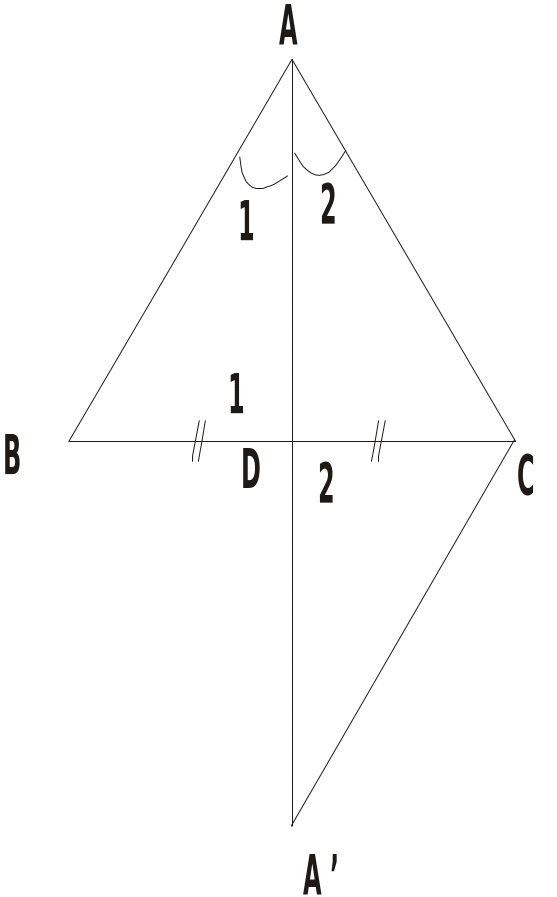
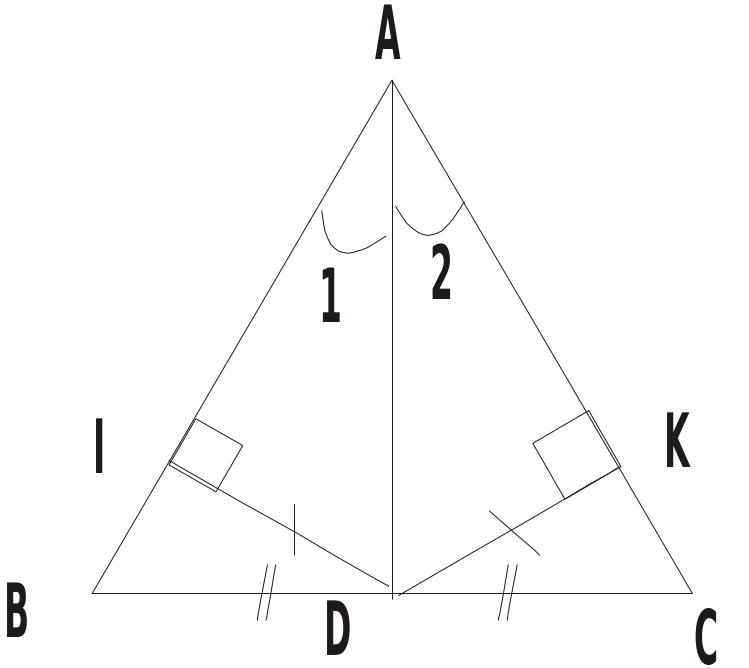











 S
hoạt động nhóm làm bài.
S
hoạt động nhóm làm bài.
 A
B
A
B

 )
Dựng hình: P
)
Dựng hình: P aùch
döïng khaùc: P
aùch
döïng khaùc: P
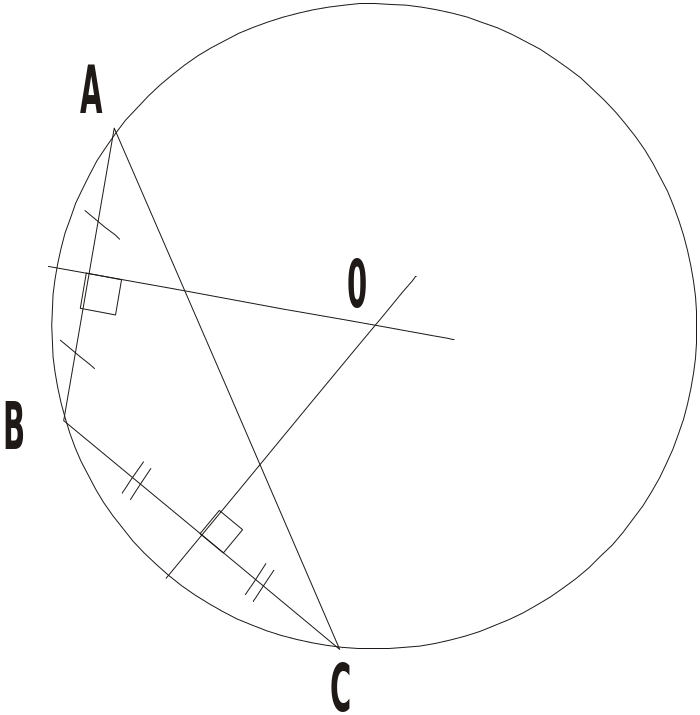
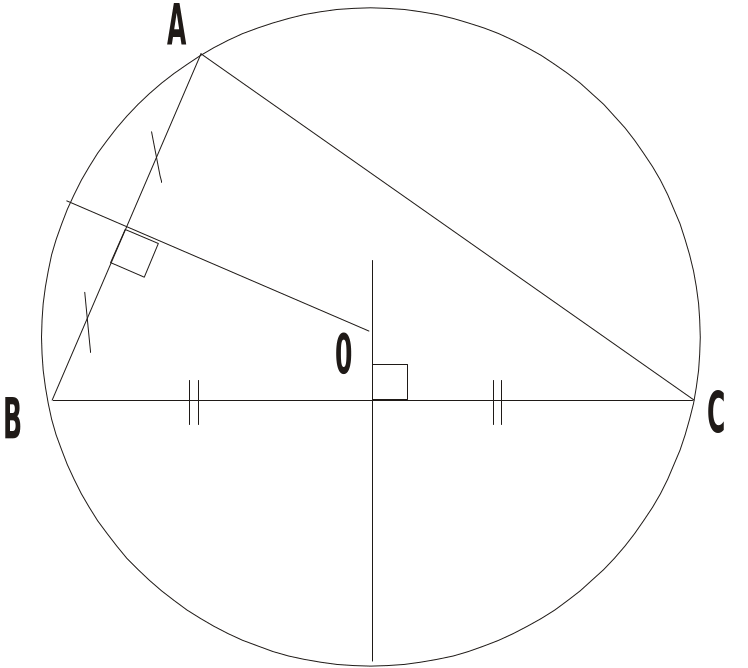
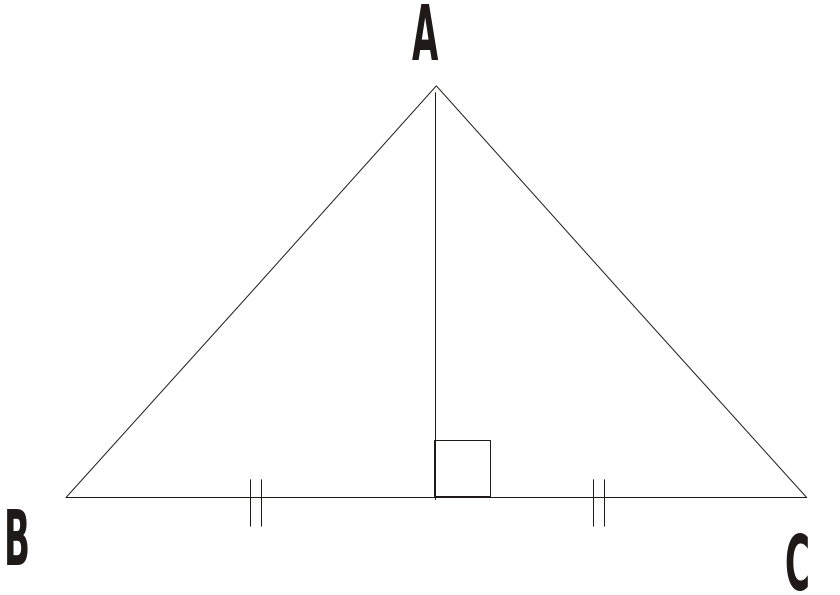
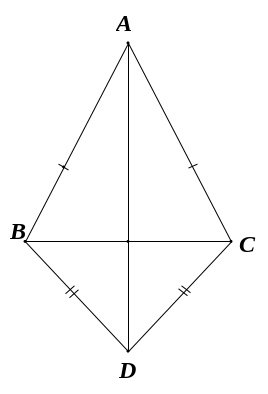



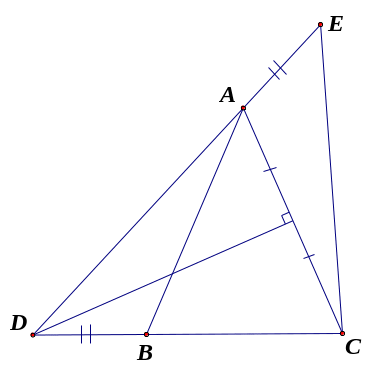

 .
.
 .
.

 .
.