leafleafleafMan illustrationFlower illustration
26 Tháng Sáu, 2023

Docly

Tìm giá trị lớn nhất, nhỏ nhất của biểu thức lớp 8 – Luyện tập

Dạng bài tìm giá trị lớn nhất, nhỏ nhất của một biểu thức là thường xuất hiện trong các bài kiểm tra môn Toán lớp 8. Trong tài liệu sau đây, Trang Tài Liệu cung cấp lý thuyết và một số dạng toán tìm giá trị lớn nhất và nhỏ nhất của biểu thức (bao gồm biểu thức chứa dấu căn và dấu giá trị tuyệt đối) nhằm giúp các em ôn tập lại khái niệm và phương pháp tìm giá trị lớn nhất và nhỏ nhất. Hãy tham khảo chi tiết trong tài liệu dưới đây.

Tìm giá trị nhỏ nhất của biểu thức lớp 8

tìm giá trị nhỏ nhất của biểu thức lớp 8

7 Hằng đẳng thức đáng nhớ

1) (A+B)2=A2+2AB+B2(A+B)2=A2+2AB+B2

2) (A−B)2=A2−2AB+B2(A−B)2=A2−2AB+B2

3) A2−B2=(A−B)(A+B)A2−B2=(A−B)(A+B)

4) (A+B)3=A3+3A2B+3AB2+B3(A+B)3=A3+3A2B+3AB2+B3

5) (A−B)3=A3−3A2B+3AB2−B3(A−B)3=A3−3A2B+3AB2−B3

6) A3+B3=(A+B)(A2−AB+B2)A3+B3=(A+B)(A2−AB+B2)

7) A3−B3=(A−B)(A2+AB+B2)A3−B3=(A−B)(A2+AB+B2)

Bài tập tìm giá trị nhỏ nhất của biểu thức – Toán lớp 8

Ví dụ 1: Tìm giá trị nhỏ nhất của biểu thức: A=x2−4x+7A=x2−4x+7

Giải

Ta có :A=x2−4x+7=(x2−2⋅2⋅x+4)+3=(x−2)2+3:A=x2−4x+7=(x2−2⋅2⋅x+4)+3=(x−2)2+3

Ta luôn có : (x−2)2≥0(x−2)2≥0 với mọi xx.

Suy ra: (x−2)2+3≥3(x−2)2+3≥3 với mọi xx.

hay A≥3A≥3 với mọi xx.

Dấu “=” xảy ra khi : x−2=0x−2=0 hay x=2x=2

Nên : Amin=3Amin=3 khi x=2x=2

Ví dụ 2: Chứng minh rằng biểu thức sau luôn dương với mọi xx.

B=4x2+4x+3B=4x2+4x+3

Giải

Ta có: B=(2x)2+2⋅2x⋅1+12+2=(2x+1)2+2B=(2x)2+2⋅2x⋅1+12+2=(2x+1)2+2

Ta luôn có: (2x+1)2≥0(2x+1)2≥0 với mọi xx.

Suy ra: (2x+1)2+2≥2>0(2x+1)2+2≥2>0 với mọi xx.

Hay: B>0B>0 với mọi xx.

Vậy: biểu thức BB luôn dương với mọi xx

Ví dụ 3: Tìm giá trị nhỏ nhất của biểu thức :

C=x2+9y2+6x−6y+5C=x2+9y2+6x−6y+5

Giải

Ta có : C=x2+9y2+6x−6y+5C=x2+9y2+6x−6y+5

=(x2+2⋅x⋅3+9)+(9y2−2⋅3y⋅1+1)−5=(x+3)2+(3y−1)2−5=(x2+2⋅x⋅3+9)+(9y2−2⋅3y⋅1+1)−5=(x+3)2+(3y−1)2−5

Mà : (x−2)2≥0;(3y−1)2≥0(x−2)2≥0;(3y−1)2≥0 với mọi x,yx,y.

(x−2)2+(3y−1)2≥0(x−2)2+(3y−1)2≥0 với mọi x,yx,y

Suy ra: (x+3)2+(3y−1)2−5≥−5(x+3)2+(3y−1)2−5≥−5 với mọi x,yx,y.

hay: C≥−5C≥−5 với mọi x,yx,y

Dấu “=” xảy ra khi : x+3=0x+3=0 và 3y−1=03y−1=0

x=−3x=−3 và y=13y=13

Nên: Cmin=−5Cmin=−5 khi x=−3x=−3 và y=13y=13



Mở rộng Tìm giá trị nhỏ nhất của biểu thức lớp 8

Khái niệm 

Trong môn Toán lớp 8, để tìm giá trị lớn nhất hoặc nhỏ nhất của một biểu thức, ta cần áp dụng các phương pháp và công thức tương ứng với từng loại biểu thức. Các biểu thức có thể chứa dấu căn, dấu giá trị tuyệt đối, biến số, hàm số, đa thức,… và chúng ta cần phải biết cách phân tích, đơn giản hoá biểu thức trước khi áp dụng phương pháp tìm giá trị lớn nhất hoặc nhỏ nhất.

Phương pháp

Các phương pháp thường được áp dụng bao gồm: sử dụng đạo hàm, áp dụng bất đẳng thức, chia biểu thức ra thành các tổng, tích,… và sử dụng các kiến thức cơ bản về số học và đại số. Để tìm giá trị lớn nhất của biểu thức, ta cần tìm giá trị lớn nhất của biểu thức trong miền giá trị xác định. Tương tự, để tìm giá trị nhỏ nhất của biểu thức, ta cần tìm giá trị nhỏ nhất của biểu thức trong miền giá trị xác định.

Việc tìm giá trị lớn nhất, nhỏ nhất của một biểu thức là một kỹ năng cần thiết trong môn Toán lớp 8 và cũng là một trong những dạng bài kiểm tra thường gặp.

I. Dạng 1: Tam thức bậc hai

Phương pháp: Đối với dạng tam thức bậc hai ta đưa biểu thức đã cho về dạng bình phương một tổng (hoặc hiệu) cộng (hoặc trừ) đi một số tự do.

Tổng quát: 

  • d – (a ± b)2 ≤ d Ta tìm được giá trị lớn nhất
  • (a ± b)2± c ≥ ± c  Ta tìm được giá trị nhỏ nhất

Lời giải

Ta có:

B = 6 – 8x – x2 = -(x2 + 8x) + 6

= -(x2 + 8x + 16) + 6 + 16

= -(x + 4)2 + 22

Vì (x +4)2 ≥ 0 ⇒ -(x +4)2 ≤ 0 ⇒ -(x +4)2 + 22 ≤ 22

Do đó, giá trị lớn nhất của biểu thức B là 22

Ví dụ 2. Tìm giá trị nhỏ nhất của biểu thức C = 4x2 + 8x + 10

Lời giải

C = 4x2 + 8x + 10 = (2x)2 + 2.2x.2 + 4 + 6

= (2x + 2)2 + 6

Với mọi x ta có: (2x + 2)2 ≥ 0 ⇒ (2x + 2)2 + 6 ≥ 6

Do đó, giá trị nhỏ nhất của biểu thức C là 6

Ví dụ 3:

a, Tìm giá trị nhỏ nhất của A = 2x2 – 8x + 1

b, Tìm giá trị lớn nhất của B = -5x2 – 4x + 1

Lời giải:

a, A = 2(x2 – 4x + 4) – 7 = 2(x – 2)2 – 7 ≥ -7

min A = -7 khi và chỉ khi x = 2

b, B = - 5\left( {{x^2} + \frac{4}{5}x} \right) + 1 = - 5\left( {{x^2} - 2.x.\frac{2}{5} + \frac{4}{{25}}} \right) + \frac{9}{5} = \frac{9}{5} - 5{\left( {x + \frac{2}{5}} \right)^2} \le \frac{9}{5}

maxB = \frac{9}{5} \Leftrightarrow x = - \frac{2}{5}

Ví dụ 4: Cho tam thức bậc hai P(x) = ax2 + bx + c

a, Tìm min P nếu a > 0

b, Tìm max P nếu a < 0

Lời giải:

Ta có P = a\left( {{x^2} + \frac{b}{a}x} \right) + c = a{\left( {x + \frac{b}{{2a}}} \right)^2} + \left( {c - \frac{{{b^2}}}{{4a}}} \right)

Đặt k = c - \frac{{{b^2}}}{{4a}}. Do {\left( {x + \frac{b}{{2a}}} \right)^2} \ge 0nên:

a, Nếu a > 0 thì a{\left( {x + \frac{b}{{2a}}} \right)^2} \ge 0do đó  P ≥ k ⇒ min P = k

b, Nếu a < 0 thì a{\left( {x + \frac{b}{{2a}}} \right)^2} \le 0do đó P ≤ k ⇒ max P = k ⇒ x = \frac{{ - b}}{{2a}}

Bài tập vận dụng

Bài tập: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức dưới đây:

a, A = -x2 + x + 1 b, B = x2 + 3x + 4
c, C = x2 – 11x + 30 d, D = x2 – 2x + 5
e, E = 3x2 – 6x + 4 f, F = -3x2 – 12x – 25

II. Dạng 2: Đa thức có dấu giá trị tuyệt đối

Phương pháp: Có hai cách để giải bài toán này:

Cách 1: Dựa vào tính chất |x| ≥ 0. Ta biến đổi biểu thức A đã cho về dạng A ≥ a (với a là số đã biết) để suy ra giá trị nhỏ nhất của A là a hoặc biến đổi về dạng A ≤ b (với b là số đã biết) từ đó suy ra giá trị lớn nhất của A là b.

Cách 2: Dựa vào biểu thức chứa hai hạng tử là hai biểu thức trong dấu giá trị tuyệt đối. Ta sẽ sử dụng tính chất:

∀x, y ∈ \mathbb{Q} ta có:

  • \left | x+y \right |\leq\left | x\right | +\left | y\right |
  • \left | x-y \right |\leq\left | x\right | -\left | y\right |

Ví dụ 1: Tìm giá trị nhỏ nhất của các biểu thức sau:

a. A = (3x – 1)2 – 4|3x – 1| + 5

b. B = |x – 2| + |x – 3|

Lời giải:

a, A = {\left( {3x - 1} \right)^2} - 4\left| {3x - 1} \right| + 5

Đặt y = \left| {3x - 1} \right| \Rightarrow A = {y^2} - 4y + 5 = {\left( {y - 2} \right)^2} + 1 \ge 1

min A = 1\Leftrightarrow y = 2 \Leftrightarrow \left| {3x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}3x - 1 = 2\\3x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{{ - 1}}{3}\end{array} \right.

b, B = \left| {x - 2} \right| + \left| {x - 3} \right|

B = \left| {x - 2} \right| + \left| {x + 3} \right| \ge \left| {x - 2 + 3 - x} \right| = 1

\Rightarrow \min B = 1 \Leftrightarrow \left( {x - 2} \right)\left( {3 - x} \right) \ge 0 \Leftrightarrow 2 \le x \le 3

Ví dụ 2: Tìm giá trị nhỏ nhất của C = |x2 – x + 1| + |x2 – x – 2|

Hướng dẫn giải

Ta có:

C = |x2 – x + 1| + |x2 – x – 2| ≥ |x2 – x + 1 + 2 + x – x2| = 3

MinC = 3 ⇔ (x2 – x + 1)(2 + x – x2) ≥ 0 ⇔ (x + 1)(x – 2) ≤ 0 ⇔ -1 ≤ x ≤ 2

Ví dụ 3: Tìm giá trị nhỏ nhất của T = |x – 1| + |x – 2| + |x – 3| + |x – 4|

Hướng dẫn giải

Ta có |x – 1| + |x – 4| ≥ |x – 1 + 4 – x| = 3 (1)

Và |x – 2| + |x – 3| ≥ |x – 2 +3 – x| = 1(2)

Vậy T ≥ 1 + 3 = 4

Từ (1) suy ra dấu bằng xảy ra khi 1 ≤ x ≤ 4

Từ (2) suy ra dấu bằng xảy ra khi 2 ≤ x ≤ 3

Vậy T có giá trị nhỏ nhất bằng 4 khi 2 ≤ x ≤ 3

Bài tập vận dụng: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức dưới đây:

A = |x – 2004| + |x – 2005|

B = |x – 2| + |x – 9| + 1945

C = -|x – 7| – |y + 13| + 1945

III. Dạng 3: Đa thức bậc cao

  • Dạng phân thức
  • Phân thức có tử là hằng số, mẫu là tam thức bậc hai
  • Các phân thức có dạng khác

Ví dụ 1: Tìm giá trị nhỏ nhất của các đa thức sau:

a. A = x(x – 3)(x – 4)(x – 7)

b. B = 2x2 + y2 – 2xy – 2x + 3

c. C = x2 + xy + y2 – 3x – 3

Lời giải:

a, A = x(x – 3)(x – 4)(x – 7) = (x2 – 7x)(x2 – 7x + 12)

Đặt y = x2 – 7x + 6 thì A = (y – 6)(y + 6) = y2 – 36 ≥ -36

MinA = - 36 \Leftrightarrow y = 0 \Leftrightarrow {x^2} + 7x + 6 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = 6 \end{array} \right.

b, B = 2x2 + y2 – 2xy – 2x + 3 = (x2 – 2xy + y2) + (x2 – 2x + 1) + 2

= {\left( {x - y} \right)^2} + {\left( {x - 1} \right)^2} + 2 \ge 2 \Leftrightarrow \left\{ \begin{array}{l} x - y = 0\\ x - 1 = 0 \end{array} \right. \Leftrightarrow x = y = 1

c, C = x2 + xy + y2 – 3x – 3 = x2 – 2x + y2 – 2y + xy – x – y

Ta có C + 3 = \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 2y + 1} \right) + \left( {xy - x - y + 1} \right)

= {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + \left( {x - 1} \right)\left( {y - 1} \right) Đặt a = x - 1;b = y - 1 thì

C + 3 = {a^2} + {b^2} + ab = \left( {{a^2} + 2.a.\frac{b}{2} + \frac{{{b^2}}}{4}} \right) + \frac{{3{b^2}}}{4} = {\left( {a + \frac{b}{2}} \right)^2} + \frac{{3{b^2}}}{4} \ge 0

Vậy Min(C + 3) = 0 hay min C = -3⇔ a = b = 0 ⇔ x = y = 1

C. Bài tập vận dụng

1. Bài tập trắc nghiệm

Câu 1. Tìm giá trị lớn nhất của biểu thức B = 10 – x2

A.0     B.10        C. -10         D. 9

Đáp án

Ta có: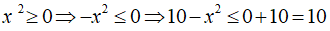

Do đó, giá trị lớn nhất của biểu thức B là 10

Chọn B.

Câu 2. Tìm giá trị lớn nhất của biểu thức A = 4x – 2×2

A.0

B. 1

C. 4

D. 2

Đáp án

Ta có;

A = 4x – 2×2 = -2(x2 – 2x)

= -2(x2 – 2x + 1) + 2 = -2(x – 1)2 + 2

Vì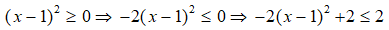

Do đó, giá trị lớn nhất của biểu thức A là 2.

Chọn D.

Câu 3 . Tìm giá trị lớn nhất của biểu thức C = 4x + 3 – x2

A.7

B. 4

C. 3

D. -1

Đáp án

Ta có:

Vì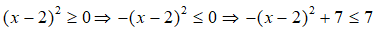

Do đó, giá trị lớn nhất của C là 7.

Chọn A.

Câu 4. Tìm giá trị lớn nhất của biểu thức D = -x2 + 6x – 11

A.-11 B. 6 C. -2 D. 9

Đáp án

D = -x2 + 6x – 11 = -(x2 – 6x) – 11

= -(x2 – 6x + 9) + 9 – 11

= -(x – 3)2 – 2

Vì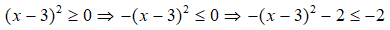

Giá trị lớn nhất của biểu thức D là – 2

Chọn C

Câu 5. Tìm giá trị lớn nhất của biểu thức E = 4x – x2 + 1

A.1 B. 5 C. 3 D. 6

Đáp án

Ta có:

E = 4x – x2 + 1 = -(x2 – 4x) + 1

= -(x2 – 4x + 4) + 4 + 1

= -(x – 2)2 + 5

Vì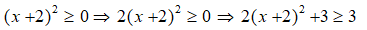

Do đó, giá trị lớn nhất của biểu thức E là 5.

Chọn B.

Câu 6. Tìm giá trị nhỏ nhất của biểu thức A = 2×2 + 8x + 11

A.3 B. 8 C. 11 D. 9

Đáp án

Ta có:

A = 2×2 + 8x + 11 = 2(x2 + 4x) + 11

= 2(x2 + 4x + 4) – 8 + 11

= 2(x + 2)2 + 3

Vì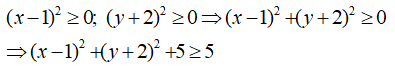

Vậy giá trị nhỏ nhất của biểu thức A là 3

Chọn A.

Câu 7. Tìm giá trị nhỏ nhất của biểu thức E = x2 – 2x + y2 + 4y + 10

A.1 B. 10 C. 5 D. 8

Đáp án

Ta có:

E = x2 – 2x + y2 + 4y + 10

= (x2 – 2x + 1) + (y2 + 4y + 4) + 5

= (x – 1)2 + (y + 2)2 + 5

Vì

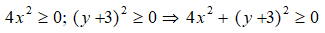
Do đó, giá trị nhỏ nhất của E là 5.

Chọn C.

Câu 8. Tìm giá trị nhỏ nhất của biểu thức D = 4×2 + y2 + 6y + 20

A. 20 B. 11 C. 10 D. 16

Đáp án

Ta có;

D = 4×2 + y2 + 6y + 20 = 4×2 + (y2 + 6y + 9) + 11

= 4×2 + (y + 3)2 + 11

Vì: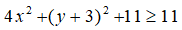

Suy ra:

Vậy giá trị nhỏ nhất của D là 11

Chọn B.

Câu 9. Tìm giá trị nhỏ nhất của biểu thức G = x2 + 5y2 – 4xy – 8y + 28

A.10 B. 8 C. 20 D. 15

Đáp án

Ta có:

G = x2 + 5y2 – 4xy – 8y + 28

G = (x2 – 4xy + 4y2) + (y2 – 8y + 16) + 8

= (x – 2y)2 + (y – 4)2 + 8

Vì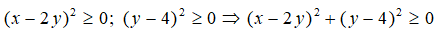

Suy ra: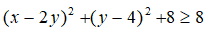

Vậy giá trị nhỏ nhất của G là 8.

Chọn B.

2. Bài tập tự luận:

Bài tập 1: Tìm giá trị nhỏ nhất của biểu thức:

a, A = 2{x^2} + 2xy + {y^2} - 2x + 2y + 2

b, B = {x^4} - 8xy + {x^3}y + {x^2}{y^2} - x{y^3} + {y^4} + 200

c, C = {x^2} + xy + {y^2} - 3x - 3y

d, D = x\left( {x + 1} \right)\left( {{x^2} + x - 4} \right)

Bài tập 2: Tìm giá trị lớn nhất của biểu thức:

A = - {x^2} - {y^2} + xy + 2x + 2y

Trangtailieu.com đã cung cấp tài liệu về Tìm giá trị lớn nhất, nhỏ nhất của biểu thức để giúp các em học sinh nắm được những dạng toán cơ bản và phát triển kỹ năng giải bài tập. Để đạt kết quả tốt hơn, các em cần thực hành giải nhiều dạng bài tập khác nhau. Chúc các em học tốt!

Bài viết liên quan

Các trường hợp đồng dạng của tam giác & Bài tập liên quan

0 lượt xem

Lược đồ Hoocne & Bài tập vận dụng lược đồ Horner vào giải toán

31 lượt xem

Nội dung mới nhất

Blog

0 lượt xem

Chính sách bảo mật

0 lượt xem

Về chúng tôi

0 lượt xem

Liên Hệ

0 lượt xem

Ma Trận Đề Thi Giữa Kì 1 Tiếng Anh 9 Chương Trình 7 Năm (2 Kỹ Năng) Năm Học 2020-2021

0 lượt xem

Phiếu Bài Tập Toán 9 Tuần 11 Có Lời Giải Chi Tiết - Toán 9

0 lượt xem

Tổng Hợp Các Đề Thi Vào Lớp 10 Môn Văn Có Đáp Án [2023]

0 lượt xem

Bài Tập Chuyên Đề Passive Voice-Câu Bị Động Có Đáp Án Ôn Thi Vào Lớp 10

0 lượt xem

Đề Thi Tiếng Anh Giữa Kì 1 Năm 2022-2023 Kèm Lời Giải Chi Tiết

0 lượt xem

Tài Liệu Bồi Dưỡng Học Sinh Giỏi Ngữ Văn 9 Cả Năm - Ngữ Văn Lớp 9

0 lượt xem

Cung cấp bởi @Trangtailieu