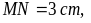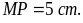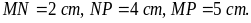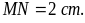Giải Toán Lớp 6 Hình Học Bài 2 Hình Chữ Nhật Hình Thoi Hình Bình Hành Hình Thang Cân
Giải Toán Lớp 6 Hình Học Bài 2 Hình Chữ Nhật Hình Thoi Hình Bình Hành Hình Thang Cân Chân Trời Sáng Tạo – Toán 6 Chân Trời Sáng Tạo là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
BÀI 2. HÌNH CHỮ NHẬT – HÌNH THOI
HÌNH BÌNH HÀNH – HÌNH THANG CÂN
A. KIẾN THỨC CẦN NHỚ

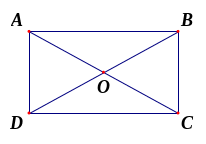
Hình
chữ nhật
-
Bốn đỉnh
-
Hai cặp cạnh
đối diện
bằng nhau:
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD. -
Bốn góc
đỉnh
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:
|
Đỉnh Đường chéo
Cạnh |

Hình
thoi -
Bốn đỉnh
- Bốn cạnh bằng nhau:
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD. - Hai đường chéo AC và BD vuông góc với nhau. |
Đường chéo
|
Hình
bình hành -
Bốn đỉnh
-
Hai cặp cạnh
đối diện
bằng nhau:
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD. - Hai cặp góc đối diện bằng nhau: góc đỉnh A bằng góc đỉnh C, góc đỉnh B bằng góc đỉnh D. -
Hai đường
chéo cắt
nhau tại trung điểm của mỗi đường:
|
|
Hình
thang
cân
- Hai cạnh đáy song song: AB song song với CD. -
Hai cạnh bên
bằng nhau:
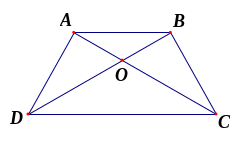
- Hai góc kề một đáy bằng nhau: góc đỉnh A bằng góc đỉnh B, góc đỉnh C bằng góc đỉnh D. -
Hai đường
chéo
bằng nhau:
|
Cạnh bên
Cạnh đáy
|
B. BÀI TẬP CÓ HƯỚNG DẪN. (MẪU TỰ LUẬN)
DẠNG 1: Dạng tính độ dài các cạnh, đường chéo của một hình phẳng
Bài
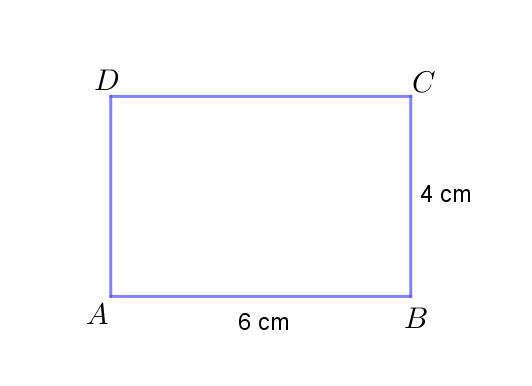
1. Cho
hình chữ nhật ABCD có
|
|
Hướng dẫn: Ta
có:
|
|
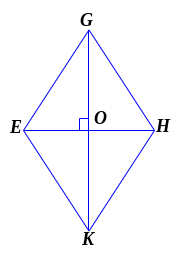
Bài
2. Cho
hình thoi EGHK với O là giao điểm của hai đường chéo.
Biết
|
|
Hướng dẫn: Ta
có:
|
|
Bài
3. Cho
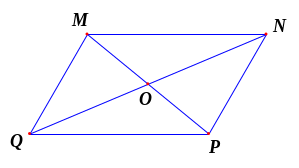
hình bình hành MNPQ có O là giao điểm
của hai đường chéo và thỏa mãn
|
|
Hướng dẫn: Ta
có:
|
|
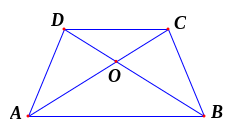
Bài
4. Cho
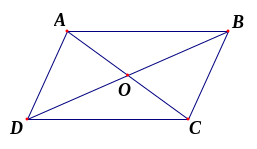
hình thang cân ABCD
với cạnh đáy là AB và CD. Biết
|
|
Hướng dẫn: Ta
có:
|
|
DẠNG 2: Vẽ một hình phẳng cho trước khi biết độ dài các cạnh và độ dài đường chéo.
Bài
1. Nêu
cách vẽ hình chữ nhật ABCD với
Hướng dẫn: -
Dùng thước thẳng vẽ đoạn thẳng
-
Dùng êke và thước kẻ đường BC vuông góc với AB tại
B và BC = 3 cm, sau đó kẻ đường AD vuông góc với AB
tại A và
- Nối D và C ta được tứ giác ABCD là hình chữ nhật cần vẽ. |
|
|
|
B |
|
Hướng dẫn: -
Dùng thước thẳng vẽ đoạn thẳng
- Dùng compa vẽ đường tròn tâm M bán kính 3 cm rồi vẽ đường tròn tâm P bán kính 3 cm. Hai đường tròn trên cắt nhau tại hai điểm N và Q. - Nối N và M, nối N với P, nối Q với M, Q với P ta được tứ giác MNPQ là hình thoi cần vẽ. |
|
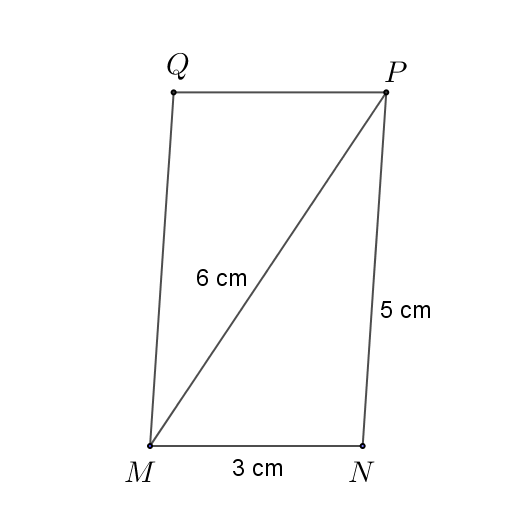
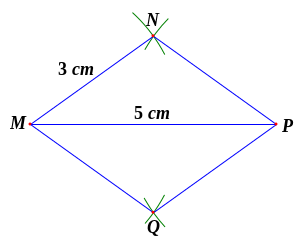
Bài
3. Nêu
cách vẽ hình bình hành MNPQ thỏa mãn
|
|
Hướng dẫn: -
Dùng thước thẳng vẽ đoạn thẳng
- Dùng compa vẽ một phần đường tròn tâm M bán kính 5 cm. Vẽ một phần đường tròn tâm N bán kính 4 cm. Hai phần đường tròn trên cắt nhau tại điểm P. -
Nối N và P. Từ M kẻ đường thẳng MQ song song với NP
và
- Nối P và Q ta được tứ giác MNPQ là hình bình hành cần vẽ. |
|
DẠNG 3: Toán học và đời sống
Bài 1: Một số hình ảnh được cắt ghép mà chúng ta thường gặp trong đời sống hằng ngày có dạng là hình chữ nhật. Vậy tại sao chúng lại có dạng hình chữ nhật và mục đích của việc cắt ghép này là gì? Các em cùng quan sát hình ảnh đi chợ của người dân, công tác phòng chống dịch bệnh của các y bác sĩ và lực lượng làm nhiệm vụ trong những ngày dịch bệnh ở dưới đây: |
|||
|
|
|
|
Hướng dẫn: Ảnh chụp thường có tỉ lệ 3: 4 hoặc 16 : 9 có dạng là hình chữ nhật phù hợp với hình chữ nhật của điện thoại thông minh nên facebook đưa ra ứng dụng ghép ảnh để các bức ảnh được hiển thị đầy đủ hơn so với các hình phẳng khác mà ta biết. Việc ghép ảnh này cũng giúp người dùng truyền tải thông tin nhanh nhất đến người đọc. |
|||
Bài 2: Ở các thành phố lớn bãi đậu xe ô tô thường có dạng: hình chữ nhật, hình bình hành. Tại sao lại như vậy? Mục đích ý nghĩa của việc làm này là gì? |
|||
|
|
||
Hướng dẫn: Giúp tiết kiệm được không gian, an toàn, thuận tiện cho việc xe ra vào. |
|||
Bài 3: Giới thiệu về thổ cẩm của một số dân tộc có họa tiết trang trí là các hình hình học. |
|||
Khmer: Trong khi thổ cẩm của các dân tộc phía Bắc thường được ghép lại bằng những mảng vải màu rồi mới thêu hoa văn lên trên, thì sản phẩm của người Khmer lại tạo hoa văn trực tiếp ngay khi dệt sợi. |
Chăm: Màu sắc nền vải được ưa chuộng là đen hay đỏ, họa tiết trang trí phần lớn có dạng hình học. |
Tày: Bố cục họa tiết theo phương pháp ô quả trám có các đường viền xung quanh tạo thành các đường diềm gãy khác. Trên cơ sở của loại bố cục hoa văn một mầu đen trên nền trắng người Tày gài mầu vào từng đoạn họa tiết, tùy trình độ thẩm mỹ, ý thích của người dệt trên khung dệt thủ công. |
|
|
|
|
|
C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.
Bài
1. Cho
hình chữ nhật ABCD có
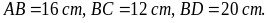 Tính
độ dài của AD, DC, AC.
Tính
độ dài của AD, DC, AC.
Đáp
án:
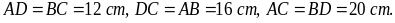
Bài
2. Cho
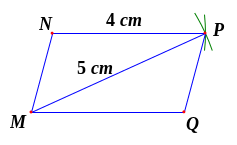
hình thoi MNPQ có
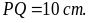 Tính
độ dài của MN, NP, MQ.
Tính
độ dài của MN, NP, MQ.
Đáp
án:
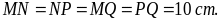
Bài
3. Cho
hình bình hành ABCD có O là giao điểm hai đường chéo và
thỏa
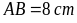 ,
,
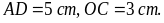 Tính độ dài của CD, BC, AC.
Tính độ dài của CD, BC, AC.
Đáp
án:
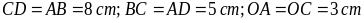 nên
nên
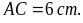
Bài
4. Cho
hình thang cân EGIH với cạnh đáy là EG và IH. Biết
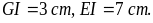
Hãy tính EH, GH.
Đáp
án:
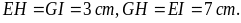
Bài 5. Hãy nêu cách ghép hai tam giác đều cùng có cạnh 4 cm thành một hình thoi.
Đáp án:
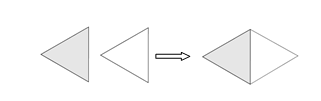
Bài 6. Hãy nêu cách ghép hình chữ nhật có chiều dài 4 cm, chiều rộng 3 cm với hai tam giác vuông có cạnh góc vuông là 3 cm và 2 cm thành một hình thang cân.
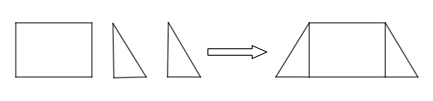
Bài
7.
Nêu cách vẽ hình chữ nhật ABCD với
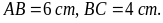
Đáp án:
Bài
8.
Nêu cách vẽ hình thoi MNPQ với
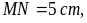 đường chéo
đường chéo
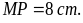
Đáp án:
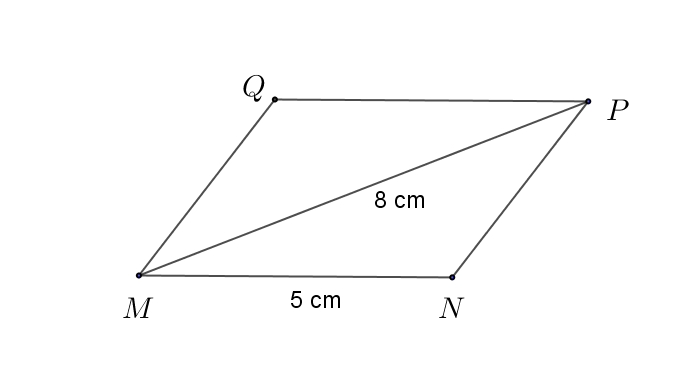
Bài
9.
Nêu cách vẽ hình bình hành MNPQ thỏa
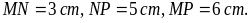
Đáp án:
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm câu trả lời sai:
A. Trong hình thoi, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
B. Trong hình thoi, hai đường chéo vuông góc với nhau.
C.
Trong
hình thoi, hai cạnh bên bằng nhau.
D.
Trong
hình thoi, hai đường chéo đường chéo bằng nhau.
Câu 2. Tìm câu trả lời sai:
A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường
B. Hình bình hành có hai góc đối bằng nhau
C.
Hình
bình hành có hai đường chéo vuông góc với nhau
D.
Hai
bình hành có hai cặp cạnh đối song
song
Câu 3. Hình thang cân có các tính chất nào sau đây?
A. Có hai đường chéo vuông góc?
B. Có bốn cạnh bằng nhau.
C.
Có
bốn cạnh song song với
nhau
D.
Có
hai góc kề một đáy bằng nhau.
Câu 4. Chọn đáp án đúng nhất?
A. Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
B. Trong hình thang cân, hai cạnh bên bằng nhau.
C.
Trong
hình thang cân, hai đường chéo bằng nhau.
D.
Cả
3 đáp án trên đều đúng.
Đáp án: 1 - D, 2 - C, 3 - D, 4 - D.
Ngoài Giải Toán Lớp 6 Hình Học Bài 2 Hình Chữ Nhật Hình Thoi Hình Bình Hành Hình Thang Cân Chân Trời Sáng Tạo – Toán 6 Chân Trời Sáng Tạo thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Bài giải toán hình học lớp 6 Bài 2 tập trung vào các hình học cơ bản như hình chữ nhật, hình thoi, hình bình hành và hình thang cân. Trong bài này, chúng ta sẽ khám phá các tính chất, công thức và cách tính diện tích, chu vi của những hình này.
Để giúp bạn hiểu rõ hơn về các hình học này, dưới đây là một số thông tin cơ bản về từng loại hình:
- Hình chữ nhật: Đây là một hình có bốn góc vuông và cạnh đối diện bằng nhau. Công thức tính chu vi của hình chữ nhật là: chu vi = 2 × (chiều dài + chiều rộng), và diện tích được tính bằng: diện tích = chiều dài × chiều rộng.
- Hình thoi: Hình thoi có bốn cạnh bằng nhau và hai đường chéo chia hình thành hai tam giác đều. Chu vi của hình thoi là tổng độ dài các cạnh, và diện tích được tính bằng: diện tích = (đường chéo dài × đường chéo ngắn) / 2.
- Hình bình hành: Đây là một hình có cạnh đối diện song song và bằng nhau. Chu vi của hình bình hành cũng là tổng độ dài các cạnh, và diện tích được tính bằng: diện tích = cạnh đáy × chiều cao.
- Hình thang cân: Hình thang cân có hai cạnh đáy bằng nhau và hai đường chéo cắt nhau tại một điểm. Chu vi của hình thang cân là tổng độ dài các cạnh, và diện tích được tính bằng: diện tích = ((đáy nhỏ + đáy lớn) × chiều cao) / 2.
Bài giải toán này sẽ cung cấp cho bạn những bài tập thực hành với các ví dụ cụ thể và câu hỏi liên quan đến tính diện tích, chu vi của các hình chữ nhật, hình thoi, hình bình hành và hình thang cân. Bằng cách thực hiện các bài tập này, bạn sẽ nắm vững các công thức và kỹ năng tính toán cơ bản trong hình học.







 có:
có: .
.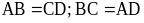 .
.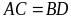 và
và
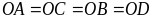



 .
.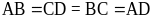 .
. Cạnh
Cạnh
 Đỉnh
Đỉnh

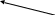
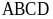 có:
có: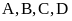 .
.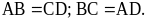
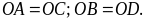

 có:
có: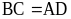 .
.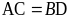 .
.



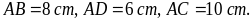
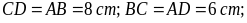
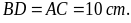
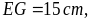
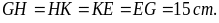
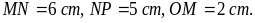
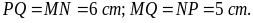
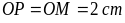
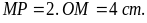
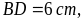
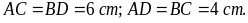
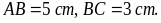
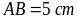
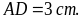
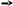

 ài
2.
ài
2.