Giá Trị Lớn Nhất Nhỏ Nhất Ôn Thi HSG Đại Số 8 Có Lời Giải Chi Tiết
Có thể bạn quan tâm
| Đề Ôn Tập Giữa Kì 2 Sử 8 Năm 2022-2023 |
Giá Trị Lớn Nhất Nhỏ Nhất Ôn Thi HSG Đại Số 8 Có Lời Giải Chi Tiết là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
DẠNG 7: GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT
Bài toán
Bài
1: Tìm giá
trị nhỏ nhất của biểu thức:
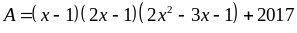
Bài
2: a) Tìm
GTLN :
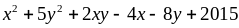
b)
Tìm GTLN :
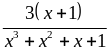
Bài
3: Cho
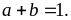 Tìm giá trị
nhỏ nhất (
Tìm giá trị
nhỏ nhất (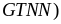 của
biểu thức
của
biểu thức
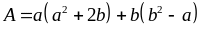
Bài
4: Cho
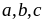 là
các số dương. Tìm giá trị nhỏ nhất của:
là
các số dương. Tìm giá trị nhỏ nhất của:
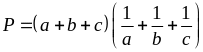
Bài
5: Cho
số thực x thỏa mãn điều kiện
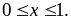 Tìm
giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm
giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
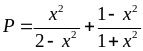
Bài
6: Tìm giá
trị nhỏ nhất của biểu thức:
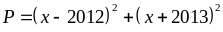
Bài
7: Tìm giá
trị nhỏ nhất của biểu thức
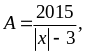 với
với
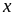 là
số nguyên.
là
số nguyên.
Bài 8: Tìm giá trị nhỏ nhất của các biểu thức:
a)
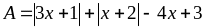 b)
b)
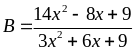
Bài
9: Tìm giá
trị nhỏ nhất của biểu thức:
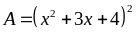
Bài
10:
Tìm giá
trị nhỏ nhất của:
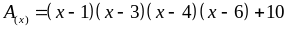
Bài
11: Tìm
giá trị nhỏ nhất của biểu thức
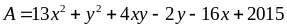
Bài 12: Tìm giá trị nhỏ nhất và lớn nhất của
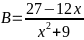
Bài
13: Tìm giá
trị nhỏ nhất của biểu thức
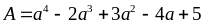
Bài
14: Tìm giá
trị nhỏ nhất của
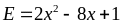
Bài 15:
Tìm giá trị nhỏ nhất của biểu thức sau:
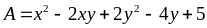
Tìm giá trị lớn nhất của biểu thức sau:
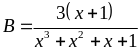
Bài
16: Tìm giá
trị nhỏ nhất của biểu thức:
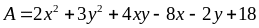
Bài
17: Tìm giá
trị lớn nhất hoặc nhỏ nhất của biểu thức sau (nếu
có):
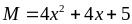
Bài
18: Tìm giá
trị nhỏ nhất của
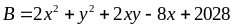
Bài
19: Cho biểu
thức
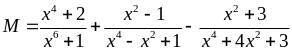
a)
Rút gọn
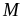
b)
Tìm giá trị lớn nhất của
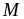
Bài
20: Cho
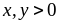 thỏa
mãn
thỏa
mãn
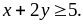 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
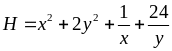
Bài 21: Tìm giá trị nhỏ nhất của biểu thức:
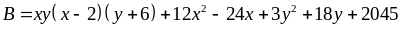
Bài
22: Tìm giá
trị nhỏ nhất của
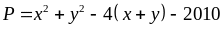
Bài
23: Cho
biểu thức
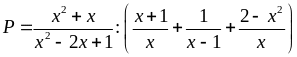
Tìm điều kiện xác định và rút gọn
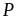
Tìm giá trị nhỏ nhất của
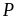 khi
khi
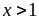
Bài
24:
Tìm giá trị nhỏ nhất của biểu thức:
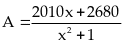
Bài
25:
Tìm giá trị
nhỏ nhất của biểu thức:
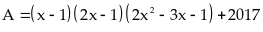
Bài
26:
Tìm giá trị lớn nhất (GTLN) của biểu thức :
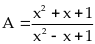
Bài 27:
Tìm giá trị nhỏ nhất của biểu thức sau:
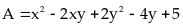
Tìm giá trị lớn nhất của biểu thức sau:
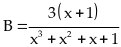
Bài
28:
Tìm giá trị nhỏ nhất của biểu thức :
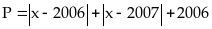
Bài
29:
Tìm giá trị nhỏ nhất của biểu thức:
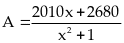
Bài
30.
Tìm giá trị nhỏ nhất của biểu thức
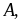 biết:
biết:
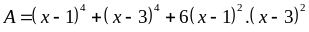
Bài
31. Cho
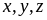 là
các số dương thỏa mãn
là
các số dương thỏa mãn
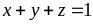
Tìm
giá trị nhỏ nhất của biểu thức:
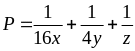
Bài
32.
Tìm giá trị nhỏ nhất :
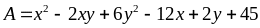
Bài
33.Tìm giá
trị lớn nhất của biểu thức:
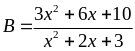
Bài 34. Cho ba số a, b, c thỏa mãn điều kiện 0 ≤ a, b, c ≤ 2 và a + b + c = 3
Tìm giá trị lớn nhất của biểu thức P = a2 + b2 + c2.
Bài
35. Tìm
giá trị lớn nhất và giá trị nhỏ nhất của biểu
thức:
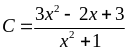 .
.
Bài
36.
Cho
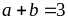 .
Tính giá trị nhỏ nhất của biểu thức
.
Tính giá trị nhỏ nhất của biểu thức
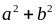
Bài
37.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu
thức:
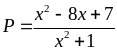
Bài
38.
Tìm giá trị lớn nhất của biểu thức
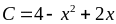
Bài
39.
Cho
các số thực dương
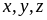 thỏa
mãn
thỏa
mãn
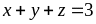
Tìm
giá trị nhỏ nhất của biểu thức
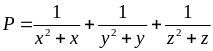
Bài
40: Cho
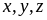 là
các số thực dương thỏa mãn:
là
các số thực dương thỏa mãn:
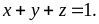
Tìm
giá trị nhỏ nhất của biểu thức:
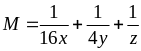
Bài
41:
Cho
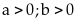 và
và
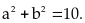 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
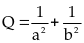
Bài 42: Tìm giá trị nhỏ nhất của biểu thức
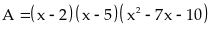
Bài
43:
Tìm giá trị nhỏ nhất của biểu thức
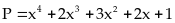
Bài
44:
Cho hai số không âm
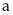 và
và
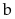 thỏa mãn:
thỏa mãn:
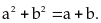 Tính
giá trị lớn nhất của biểu thức:
Tính
giá trị lớn nhất của biểu thức:
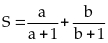
Bài
45:
Cho
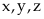 là
các số dương thỏa mãn
là
các số dương thỏa mãn
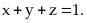 Tìm
giá trị nhỏ nhất của biểu thức
Tìm
giá trị nhỏ nhất của biểu thức
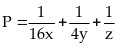
Bài
46:
Tìm giá trị nhỏ nhất của biểu thức :
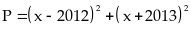
Bài 47: Tìm giá trị nhỏ nhất của biểu thức:
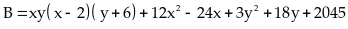
Bài
48: Cho
biểu thức
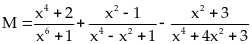
Rút gọn
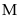
Tìm giá trị lớn nhất của
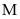
Bài
49:
Cho
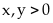 thỏa
mãn
thỏa
mãn
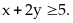 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
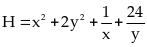
Bài
50: Tìm
giá trị nhỏ nhất của
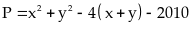
Bài
51: Cho
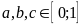 và
và
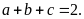 Tìm
giá trị lớn nhất của biểu thức
Tìm
giá trị lớn nhất của biểu thức
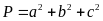
Bài
52: Tìm giá
trị nhỏ nhất của biểu thức sau:
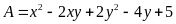
Tìm
giá trị lớn nhất của biểu thức sau:
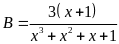
Bài
53: Tìm giá
trị nhỏ nhất của biểu thức:
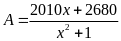
Bài
54: Tìm các
giá trị của
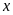 để biểu
thức:
để biểu
thức:
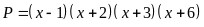 có
giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
có
giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Bài
55: Tìm giá
trị nhỏ nhất của
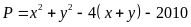
Bài
56: Tìm
giá trị nhỏ nhất của
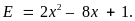
Bài 57: Tìm giá trị nhỏ nhất của M = 4x2 + 4x + 5
Bài
58:
Tìm
GTLN và GTNN của biểu thức:
![]() .
.
Bài 59: Tìm giá trị của biến x để:
a)
![]() đạt
giá trị lớn nhất
b)
đạt
giá trị lớn nhất
b)
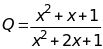 đạt
giá trị nhỏ nhất
đạt
giá trị nhỏ nhất
Bài
60:
:
a)
Tìm GTLN của
![]()
b)
Tìm GTNN của biểu thức
![]() , với
, với
![]()
Bài 61: Tìm GTNN của:
a)
![]() ; b)
; b)
![]() ;
;
c)
![]()
Bài
62:
Cho hai số x
và y thoả mãn điều kiện:
![]()
Tìm giá trị nhỏ nhất của biểu thức
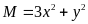 ;
;Tìm giá trị lớn nhất của biểu thức
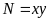
Bài
63:
a)
Cho x, y là các số dương thoả mãn
![]() .
.
Tìm
giá trị nhỏ nhất của biểu thức
![]()
b)
Tìm GTLN của
![]()
Bài
64:
a)
Cho
![]() ,
tìm giá trị nhỏ nhất của biểu thức
,
tìm giá trị nhỏ nhất của biểu thức
![]()
b)
Tìm GTNN của
![]()
Bài
65:
a)
Tìm GTNN của![]() biết
biết
![]()
b)
Tìm GTNN của
![]()
c)
Tìm GTNN của
![]()
d)
Tìm GTLN của
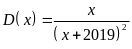 với
với
![]()
Bài
66:
Tìm
giá trị nhỏ nhất của
![]() và các giá trị của
và các giá trị của
![]() tương ứng.
tương ứng.
Bài
67: Cho
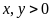 thỏa
mãn
thỏa
mãn
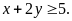 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
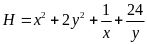 GTLN
GTLN
Bài
68: Cho
hai số không âm
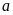 và
và
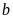 thỏa mãn:
thỏa mãn:
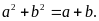 Tính
giá trị lớn nhất của biểu thức:
Tính
giá trị lớn nhất của biểu thức:
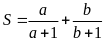
Bài
69: Cho hai
số dương
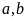 thỏa
mãn:
thỏa
mãn:
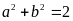
Tìm
giá trị nhỏ nhất của
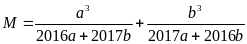
Bài
70: Cho
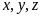 là
các số thực không âm. Tìm giá trị nhỏ nhất của:
là
các số thực không âm. Tìm giá trị nhỏ nhất của: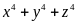 biết
biết
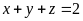
Bài
71: Tìm các
giá trị của
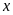 để
biểu thức:
để
biểu thức: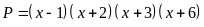 có
giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
có
giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Bài
72: Tìm giá
trị nhỏ nhất của biểu thức
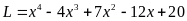
Bài
73: Tìm giá
trị nhỏ nhất của biểu thức
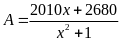
Bài
74: Tìm giá
trị nhỏ nhất của biểu thức:
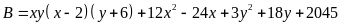
Bài
75: Cho
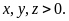 Tìm
giá trị nhỏ nhất của biểu thức :
Tìm
giá trị nhỏ nhất của biểu thức :
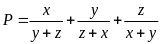
Bài
76:
Tìm GTLN và GTNN của biểu thức:
![]() .
.
Bài 77: Tìm giá trị của biến x để:
a)
![]() đạt giá trị lớn nhất b)
đạt giá trị lớn nhất b)
![]() đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất
Bài
78:
a) Tìm GTLN của
![]()
b)
Tìm GTNN của biểu thức
![]() , với
, với
![]()
Bài 79: Tìm GTNN của:
a)
![]() ; b)
; b)
![]() ; c)
; c)
![]()
Bài
80:
Cho hai số x và y thoả mãn điều kiện:
![]()
Tìm giá trị nhỏ nhất của biểu thức
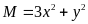 ;
;Tìm giá trị lớn nhất của biểu thức
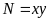
Bài
81:
a) Cho x, y là các số dương thoả mãn
![]() .Tìm
giá trị nhỏ nhất của biểu thức
.Tìm
giá trị nhỏ nhất của biểu thức
![]()
b)
Tìm GTLN của
![]()
Bài
82:
a)
Tìm GTNN của![]() biết
biết
![]()
b)
Tìm GTNN của
![]()
c)
Tìm GTNN của
![]()
d)
Tìm GTLN của
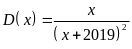 với
với
![]()
Bài
83:
:
a) Cho
![]() ,
tìm giá trị nhỏ nhất của biểu thức
,
tìm giá trị nhỏ nhất của biểu thức
![]()
b)
Tìm GTNN của
![]()
Bài
84:
Tìm
giá trị nhỏ nhất của
![]() và các giá trị của
và các giá trị của
![]() tương ứng.
tương ứng.
Bài
85:
Cho
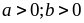 và
và
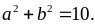 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
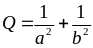
Bài
86: Tìm
giá trị nhỏ nhất của biểu thức
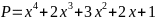
Bài
87: Cho
hai số không âm a và b thỏa mãn: a2
+ b2
= a + b. Tính giá trị lớn nhất của biểu thức:
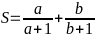
Bài
88: Cho
x,y,z là các số dương thỏa mãn x + y + z =1. Tìm giá trị
nhỏ nhất của biểu thức :
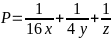
Bài
89: Tìm
giá trị nhỏ nhất của biểu thức :
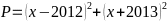
Bài
90: Tìm
giá trị nhỏ nhất của biểu thức
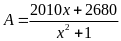
Bài
91: a. Tìm
giá trị lớn nhất của tổng x + y + z biết rằng x + 5y =
21 và 2x + 3z = 51 với x, y, z
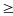 0
0
b.
Tìm giá trị nhỏ nhất, lớn nhất của các phân thức B
=
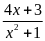
Bài
92: Tìm
giá trị nhỏ nhất của biểu thức
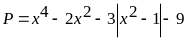 .
.
Bài
93: Tìm giá
trị lớn nhất của biểu thức
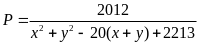
Bài
94: Cho
các số a, b,c thỏa mãn a + b + c =
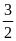 .
Tìm giá trị nhỏ nhất của biểu thức
P = a2
+ b2
+ c2
.
Tìm giá trị nhỏ nhất của biểu thức
P = a2
+ b2
+ c2
Bài
95: Cho
hai số dương
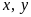 có
tổng bằng 1. Tìm giá trị nhỏ nhất của biểu thức:
có
tổng bằng 1. Tìm giá trị nhỏ nhất của biểu thức:
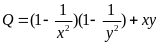
Bài
96: Tìm
giá trị nhỏ nhất của biểu thức
![]() ,
trong đó x,
y
là các số thực thoả mãn điều kiện:
,
trong đó x,
y
là các số thực thoả mãn điều kiện:
![]() .
.
Bài 97:
a)
Cho
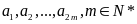 thoả mãn
thoả mãn
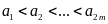 .
.
Tìm
GTNN của biểu thức
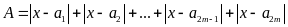 .
.
b)
Cho
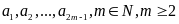 thoả mãn
thoả mãn
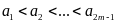 .
.
Tìm
GTNN của biểu thức
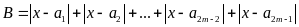 .
.
Bài 98:
Cho
m,
n
là các số thực thay đổi sao cho
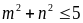 .
Hãy tìm giá trị nhỏ nhất của biểu thức:
.
Hãy tìm giá trị nhỏ nhất của biểu thức: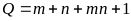 .
.
Bài
99: Tìm
giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
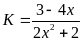
Bài
100: Cho
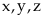 là
các số thực dương thỏa mãn:
là
các số thực dương thỏa mãn:
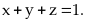
Tìm
giá trị nhỏ nhất của biểu thức:
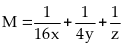
Bài
101:
Cho
các số thực dương
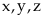 thỏa
mãn
thỏa
mãn
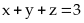
Tìm
giá trị nhỏ nhất của biểu thức
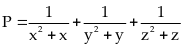
Bài
102:
Cho
hai số
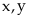 thỏa
mãn điều kiện
thỏa
mãn điều kiện
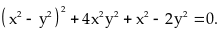 Tìm
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
Tìm
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
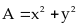
Bài
103:
Tìm
giá trị nhỏ nhất của
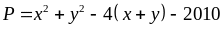
Bài
104:
Cho
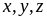 là
các số dương thỏa mãn
là
các số dương thỏa mãn
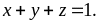
Tìm
giá trị nhỏ nhất của biểu thức :
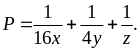
Bài
105:
Cho
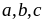 là
3 số dương thỏa mãn:
là
3 số dương thỏa mãn:
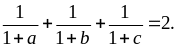 Tìm
giá trị lớn nhất của biểu thức
Tìm
giá trị lớn nhất của biểu thức
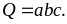
Bài
106:
Cho
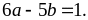 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
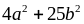
Bài
107:
Tìm giá trị nhỏ nhất của biểu thức
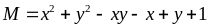
Bài
108:
Cho
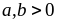 và
và
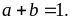 Tìm
giá trị nhỏ nhất của biểu thức:
Tìm
giá trị nhỏ nhất của biểu thức:
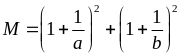
Bài 109:
Tìm giá trị nhỏ nhất của biểu thức sau:
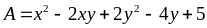
Tìm giá trị lớn nhất của biểu thức sau:
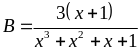
Tìm giá trị nhỏ nhất của biểu thức
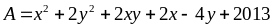
Bài
110: Tìm
giá trị nhỏ nhất của biểu thức:
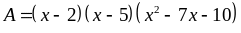
B. HƯỚNG DẪN
Bài
1: Tìm
giá trị nhỏ nhất của biểu thức
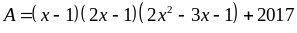
Lời giải
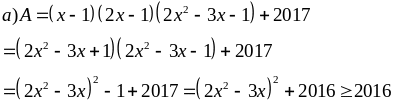
Dấu
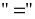 xảy
ra
xảy
ra
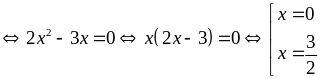
Vậy
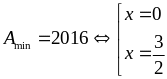
Bài
2: a) Tìm
GTLN :
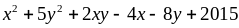
b)
Tìm GTLN :
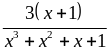
Lời giải
a)
P=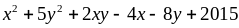
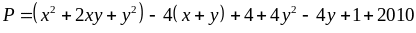
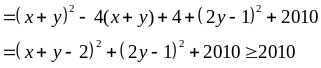
Suy
ra
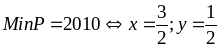
b)
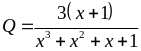
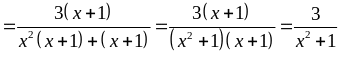
 Q
đạt GTLN
Q
đạt GTLN
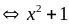 đạt
GTNN mà
đạt
GTNN mà
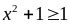
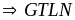 của
C là
của
C là
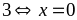
Bài
3: Cho
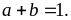 Tìm giá trị
nhỏ nhất (
Tìm giá trị
nhỏ nhất (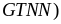 của
biểu thức
của
biểu thức
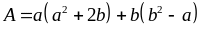
Lời giải
Do:
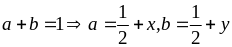 với
với
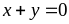
Ta
có:
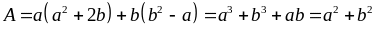
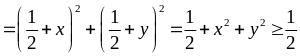
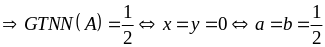
Bài
4: Cho
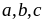 là
các số dương. Tìm giá trị nhỏ nhất của:
là
các số dương. Tìm giá trị nhỏ nhất của:
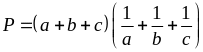
Lời giải
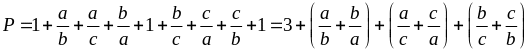
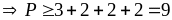
Vậy
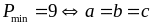
Bài
5: Cho
số thực
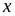 thỏa
mãn điều kiện
thỏa
mãn điều kiện
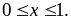 Tìm
giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm
giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
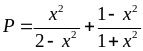
Lời giải
Đặt
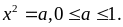 Biểu
thức đã cho trở thành:
Biểu
thức đã cho trở thành:
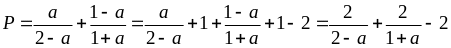
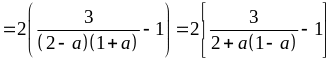
*)
Vì
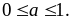
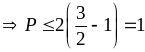
Đẳng
thức xảy ra khi
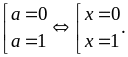
Vậy
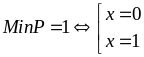
*)
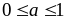 nên
nên
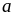 và
và
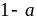 là
hai số không âm
là
hai số không âm
Áp
dụng BĐT Cô si ta có:
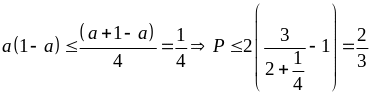
Đẳng
thức xảy ra khi
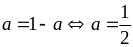 hay
hay
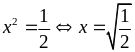
Vậy
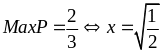
Bài
6 : Tìm
giá trị nhỏ nhất của biểu thức :
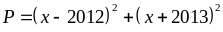
Lời giải
Ta có:
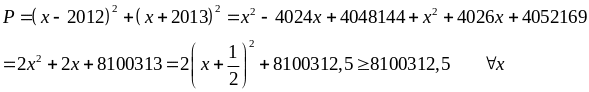
Vậy
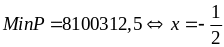
Bài
7: Tìm giá
trị nhỏ nhất của biểu thức
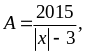 với
với
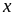 là
số nguyên.
là
số nguyên.
Lời giải
Xét
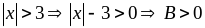
Xét
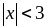 thì
do
thì
do
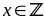 nên
nên
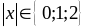
+
Khi
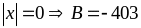
+
Khi
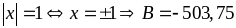
+
Khi
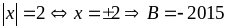
Vậy
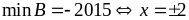
Bài 8: Tìm giá trị nhỏ nhất của các biểu thức:
a)
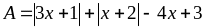 b)
b)
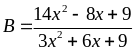
Lời giải
a)
Áp dụng tính chất
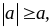 dấu
dấu
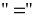 xảy
ra
xảy
ra
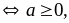 ta
có:
ta
có:
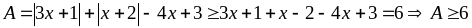
Dấu
“=” xảy ra
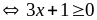 và
và
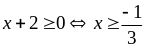 và
và
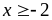
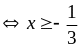
Vậy
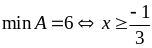
b)
Ta có
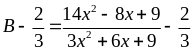
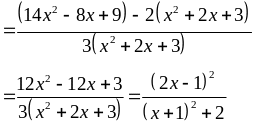
Với
mọi
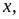 ta
có:
ta
có:
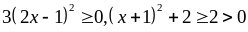
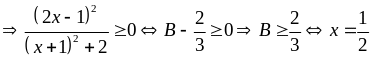
Bài
9: Tìm giá
trị nhỏ nhất của biểu thức:
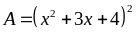
Lời giải
Ta
có:
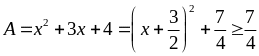
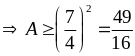 .
Dấu bằng xảy ra
.
Dấu bằng xảy ra
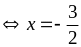
Vậy
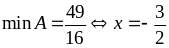
Bài
10: Tìm giá
trị nhỏ nhất của :
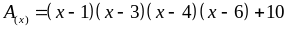
Lời giải
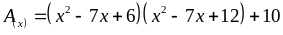
Đặt
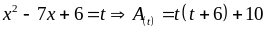
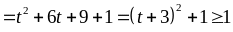
Khi
đó:
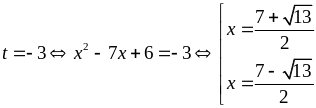
Vậy
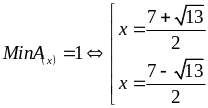
Bài
11: Tìm giá
trị nhỏ nhất của biểu thức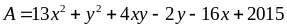
Lời giải
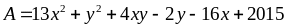
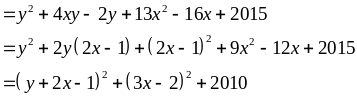
Chứng
tỏ
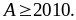 dấu
bằng xảy ra khi và chỉ khi
dấu
bằng xảy ra khi và chỉ khi
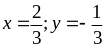
Vậy
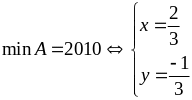
Bài
12: Tìm giá
trị nhỏ nhất và lớn nhất của
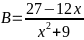
Lời giải
Ta
có:
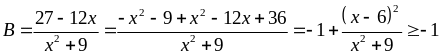
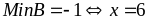
Ta
có: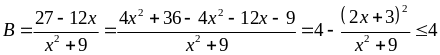
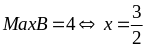
Bài
13: Tìm giá
trị nhỏ nhất của biểu thức
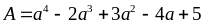
Lời giải
Biến đổi để có:
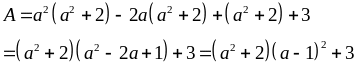
Vì
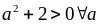 và
và
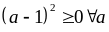 nên
nên
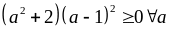
Do
đó:
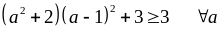
Dấu
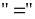 xảy
ra khi và chỉ khi
xảy
ra khi và chỉ khi
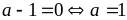
Bài
14: Tìm giá
trị nhỏ nhất của
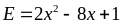
Lời giải
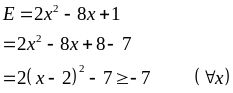
Vậy
giá trị nhỏ nhất của
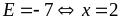
Bài
15: a) Tìm
giá trị nhỏ nhất của biểu thức sau:
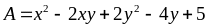
b)
Tìm giá trị lớn nhất của biểu thức sau:
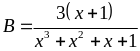
Lời giải
a) Ta có:
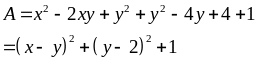
Do
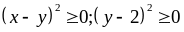 Nên
Nên
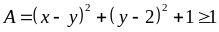
Dấu
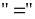 xảy
ra
xảy
ra
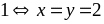
Vậy
GTNN của
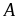 là
là
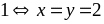
b)
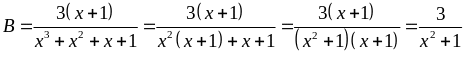
Do
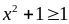 nên
nên
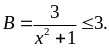 Dấu
Dấu
 xảy
ra
xảy
ra
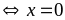
Vậy
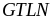 của
của
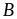 là
là
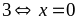
Bài
16: Tìm giá
trị nhỏ nhất của biểu thức:
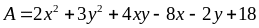
Lời giải
Ta
có:
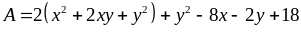
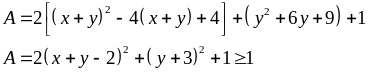
Vậy
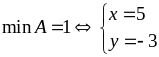
Bài
17: Tìm giá
trị lớn nhất hoặc nhỏ nhất của biểu thức sau (nếu
có):
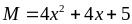
Lời giải
Ta
có
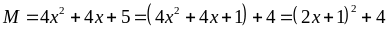
Vì
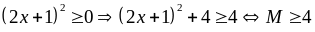
Vậy
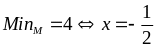
Bài
18: Tìm
giá trị nhỏ nhất của
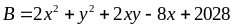
Lời giải
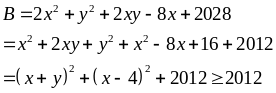
Đẳng
thức xảy ra
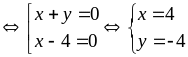
Giá
trị nhỏ nhất của B là
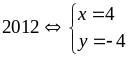
Bài
19: Cho biểu
thức
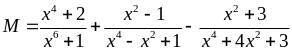
a)
Rút gọn
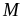 b) Tìm giá trị lớn nhất
của
b) Tìm giá trị lớn nhất
của
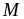
Lời giải
a)
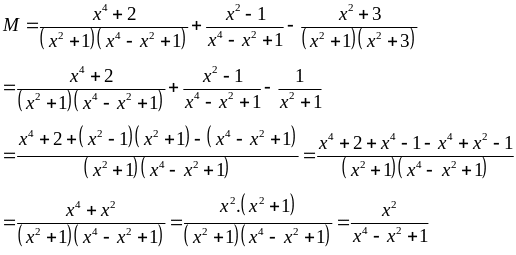
Vậy
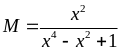 với
mọi
với
mọi
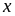
b)
Ta có :
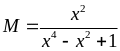 với
mọi
với
mọi
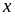
-
Nếu
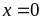 ta có
ta có
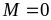
-
Nếu
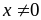 ,
chia cả tử và mẫu của
,
chia cả tử và mẫu của
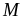 cho
cho
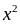 ta
có:
ta
có:
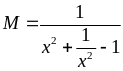
Ta
có:
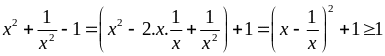
Nên
ta có:
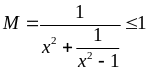 .
Dấu
.
Dấu
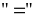 xảy
ra khi
xảy
ra khi
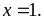
Vậy
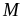 lớn
nhất là
lớn
nhất là
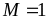 khi
khi
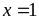
Bài
20: Cho
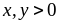 thỏa
mãn
thỏa
mãn
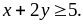 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
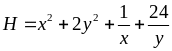
Lời giải
Ta
có:
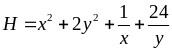
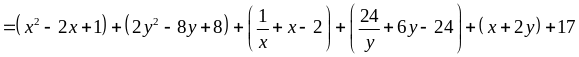
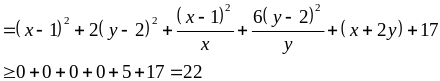
Dấu
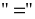 xảy
ra
xảy
ra
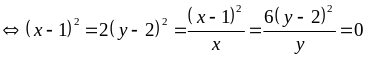 và
và
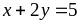
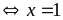 và
và
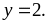 Vậy
Vậy
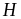 nhỏ
nhất là
nhỏ
nhất là
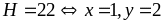
Bài 21: Tìm giá trị nhỏ nhất của biểu thức:
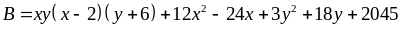
Lời giải
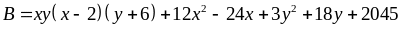
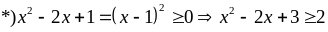 với
mọi
với
mọi

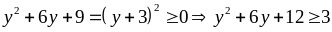 với
mọi
với
mọi
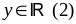
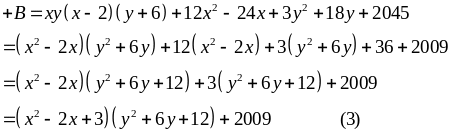
Từ
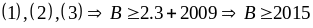
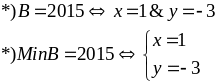
Bài
22: Tìm
giá trị nhỏ nhất của
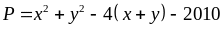
Lời giải
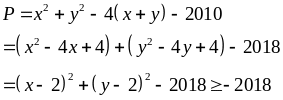
Vậy
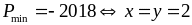
Bài
23:
Cho biểu thức
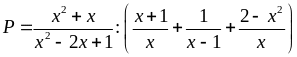
Tìm điều kiện xác định và rút gọn
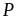
Tìm giá trị nhỏ nhất của
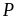 khi
khi
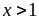
Lời giải
a)
ĐKXĐ:
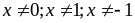
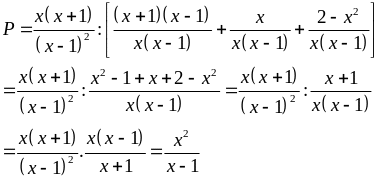
b)
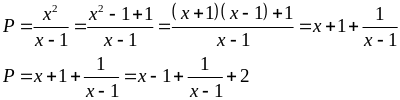
Vì
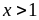 nên
nên
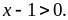 Áp
dụng BĐT Cosi ta có:
Áp
dụng BĐT Cosi ta có:
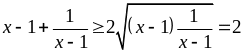
Dấu
“=” xảy ra
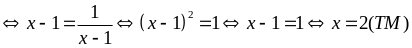
Vậy
 của
P là
của
P là
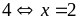
Bài
24:
Tìm
giá trị nhỏ nhất của biểu thức:
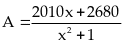
Lời giải
Ta
có:
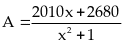
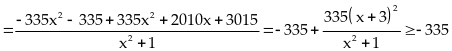
Vậy
giá trị nhỏ nhất của
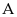 là
là
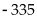 khi
khi
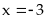
Bài
25:
Tìm giá trị nhỏ nhất của biểu thức:
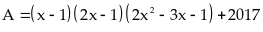
Lời giải
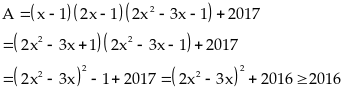
Dấu
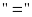 xảy
ra
xảy
ra
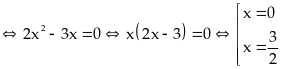
Vậy
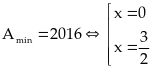
Bài
26:
Tìm giá trị lớn nhất (GTLN) của biểu thức :
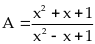
Lời giải
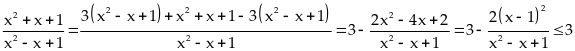 Vậy
Vậy
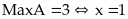
Bài 27: a) Tìm giá trị nhỏ nhất của biểu thức sau:
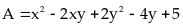
b)Tìm giá trị lớn nhất của biểu thức sau:
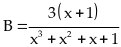
Lời giải
Ta có:
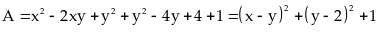
Do
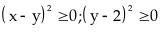 Nên
Nên
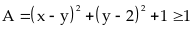
Dấu
“=” xảy ra
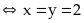
Vậy
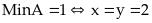
b)
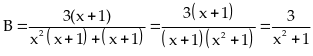
Do
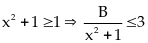 .
Đẳng thức xảy ra
.
Đẳng thức xảy ra
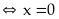
Vậy
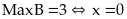
Bài
28: Tìm giá trị
nhỏ nhất của biểu thức :
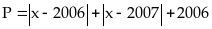
Lời giải
Ta có :
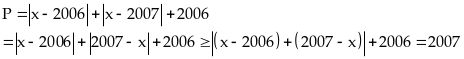
Vậy
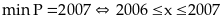
Bài
29:
Tìm giá trị nhỏ nhất của biểu thức:
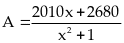
Lời giải
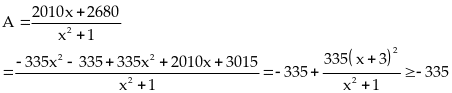
Vậy
giá trị nhỏ nhất của
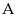 là
là
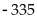 khi
khi
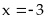
Bài
30.
Tìm giá trị nhỏ nhất của biểu thức
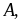 biết:
biết:
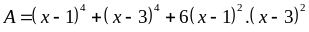
Lời giải
Đặt
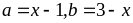 ta
có:
ta
có:
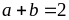
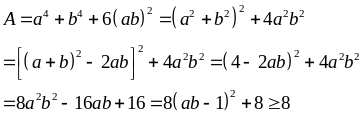
Dấu
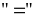 xảy
ra
xảy
ra
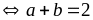 và
và
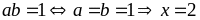
Vậy
giá trị nhỏ nhất của
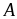 bằng 8 tại
bằng 8 tại
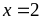
Bài 31.
Cho
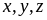 là
các số dương thỏa mãn
là
các số dương thỏa mãn
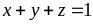
Tìm
giá trị nhỏ nhất của biểu thức:
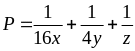
Lời giải
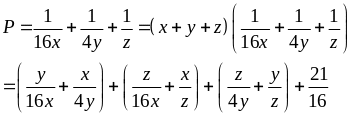
Theo
BĐT Cô si ta có:
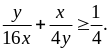 Dấu
Dấu
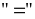 xảy
ra
xảy
ra
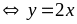
Tương
tự:
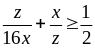 ,
dấu “=” xảy ra
,
dấu “=” xảy ra
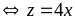
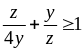 ,
dấu
,
dấu
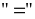 xảy
ra
xảy
ra
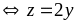
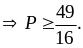 Dấu
Dấu
 xảy
ra
xảy
ra
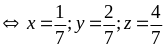
Vậy
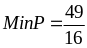 khi
với
khi
với
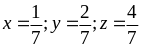
Bài
32. Tìm giá
trị nhỏ nhất :
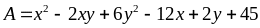
Lời giải
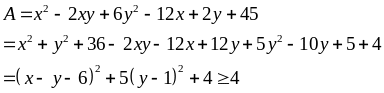
Giá
trị nhỏ nhất
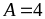 khi
khi
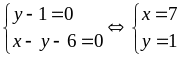
Bài
33.
Tìm giá trị lớn
nhất của biểu thức:
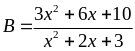
Lời giải
Ta
có:
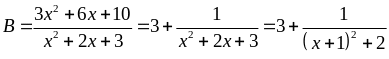
Mà
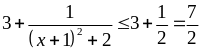
Vậy
giá trị lớn nhất của
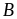 là
là
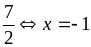
Bài 34. Cho ba số a, b, c thỏa mãn điều kiện 0 ≤ a, b, c ≤ 2 và a + b + c = 3
Tìm giá trị lớn nhất của biểu thức P = a2 + b2 + c2.
Lời giải
Từ giả thiết 0 ≤ a, b, c ≤ 2 suy ra (2 – a)(2 – b)(2 – c) + abc ≥ 0
8 – 4(a + b + c) + 2(ab + bc + ca) ≥ 0
8 – 12 + 2ab + 2bc + 2ac ≥ 0 (vì a + b + c = 3)
2ab + 2bc + 2ac ≥ 4
a2 + b2 + c2 + 2ab + 2bc + 2ac ≥ 4 + a2 + b2 + c2
( a + b + c)2 ≥ 4 + a2 + b2 + c2
a2 + b2 + c2 ≤ 5 (vì a + b + c = 3)
Dấu đẳng thức xảy ra (a; b; c) = (0; 1; 2) và các hoán vị của bộ số này.
Vậy P có GTLN nhất là 5 (a; b; c) = (0; 1; 2) và các hoán vị của bộ số này.
Bài
35. Tìm
giá trị lớn nhất và giá trị nhỏ nhất của biểu
thức:
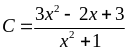 .
.
Lời giải
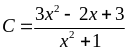 =
=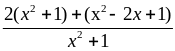 =
=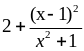 ≥ 2
≥ 2
Vậy
min C = 2
 x
= 1
x
= 1
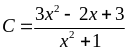 =
=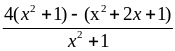 =
=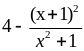 ≤ 4
≤ 4
Vậy
max C = 4
 x
= -1
x
= -1
Bài
36.
Cho
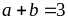 .
Tính giá trị nhỏ nhất của biểu thức
.
Tính giá trị nhỏ nhất của biểu thức
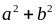
Lời giải
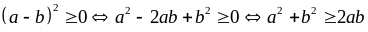 (với
mọi
(với
mọi
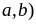
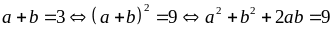
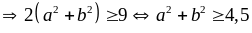
Vậy
giá trị nhỏ nhất của
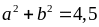
Bài
37.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu
thức:
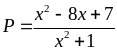
Lời giải
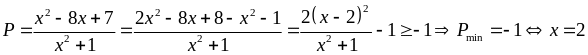
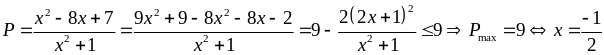
Bài
38.
Tìm giá trị lớn nhất của biểu thức
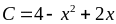
Lời giải
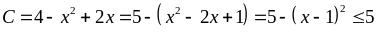
Vậy
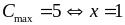
Bài
39. Cho
các số thực dương
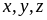 thỏa
mãn
thỏa
mãn
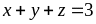
Tìm
giá trị nhỏ nhất của biểu thức
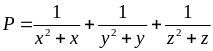
Lời giải
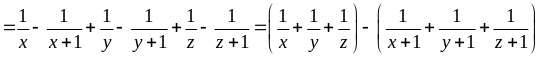
Áp
dụng BĐT
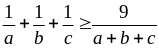 và
và
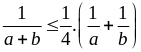 với
với
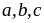 dương,
dấu bằng xảy ra
dương,
dấu bằng xảy ra
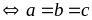
Ta
có:
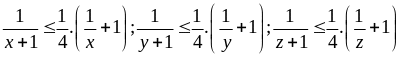
Bởi vậy :
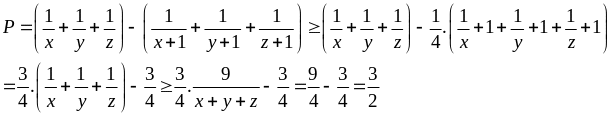
Vậy
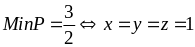
Bài
40: Cho
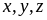 là
các số thực dương thỏa mãn:
là
các số thực dương thỏa mãn:
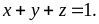
Tìm
giá trị nhỏ nhất của biểu thức:
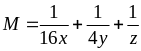
Lời giải
Vì
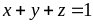 nên:
nên:
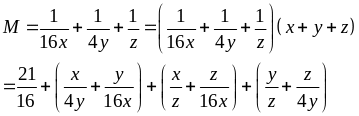
Ta có:
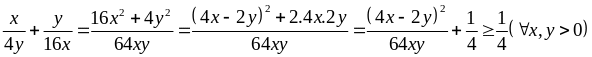
Tương
tự:
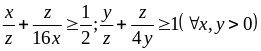
Từ
đó
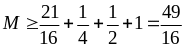 .
Dấu
.
Dấu
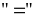 xảy
ra
xảy
ra
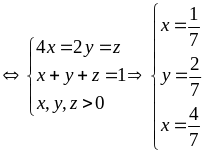
Vậy
GTNN của
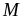 là
là
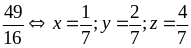
Bài
41:
Cho
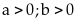 và
và
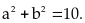 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
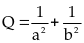
Lời giải
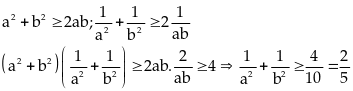
Vậy
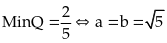
Bài 42: Tìm giá trị nhỏ nhất của biểu thức
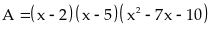
Lời giải
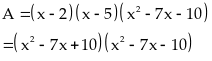
Đặt
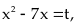 ta
có biểu thức:
ta
có biểu thức:
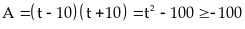
Dấu
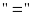 xảy
ra
xảy
ra
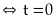
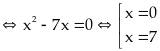
Với
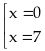 thì
thì
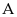 đạt
giá trị nhỏ nhất bằng
đạt
giá trị nhỏ nhất bằng
Bài
43:
Tìm giá trị nhỏ nhất của biểu thức
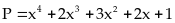
Lời giải
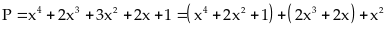
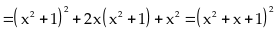
Vì
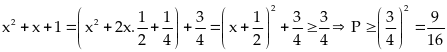
Dấu
 xảy
ra
xảy
ra
Bài
44:
Cho hai số không âm
 và
và
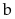 thỏa mãn:
thỏa mãn:
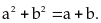 Tính
giá trị lớn nhất của biểu thức:
Tính
giá trị lớn nhất của biểu thức: 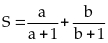
Lời giải
Ta
có:
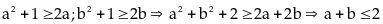
Chứng
minh được với hai số dương
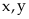 thì
thì
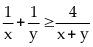
Do
đó:
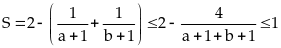
Vậy
 của
S là 1, dạt được khi
của
S là 1, dạt được khi
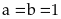
Bài
45: Cho
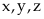 là
các số dương thỏa mãn
là
các số dương thỏa mãn
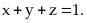 Tìm
giá trị nhỏ nhất của biểu thức
Tìm
giá trị nhỏ nhất của biểu thức
Lời giải
Ta có:
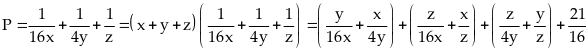 Theo
BĐT cô si ta có:
Theo
BĐT cô si ta có:
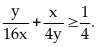 Dấu
“=” xảy ra
Dấu
“=” xảy ra
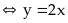
Tương
tự:
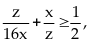 dấu
“=” xảy ra
dấu
“=” xảy ra
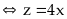
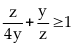 ,
dấu “=” xảy ra
,
dấu “=” xảy ra
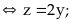
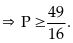 Dấu
“=” xảy ra khi
Dấu
“=” xảy ra khi
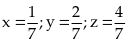
Vậy
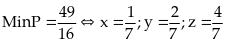
Bài
46: Tìm
giá trị nhỏ nhất của biểu thức :
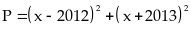
Lời giải
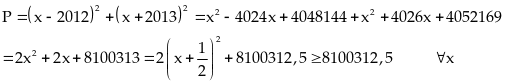
Vậy
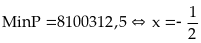
Bài 47: Tìm giá trị nhỏ nhất của biểu thức:
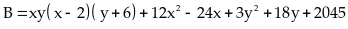
Lời giải
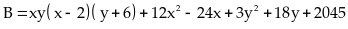
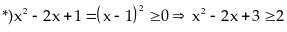 với
mọi
với
mọi

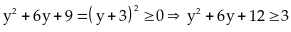 với
mọi
với
mọi
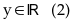
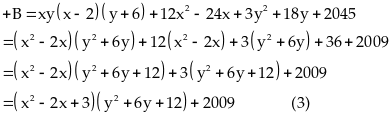
Từ
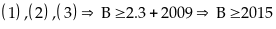
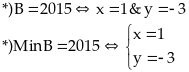
Bài
48:
Cho biểu thức
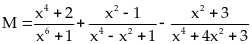
Rút gọn
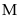
Tìm giá trị lớn nhất của
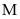
Lời giải

Vậy
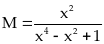 với
mọi
với
mọi
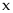
b)
Ta có :
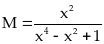 với
mọi
với
mọi
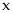
Nếu
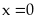 ta có
ta có
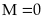
Nếu
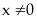 ,
chia cả tử và mẫu của
,
chia cả tử và mẫu của
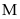 cho
cho
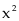 ta
có:
ta
có:
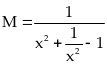
Ta
có:
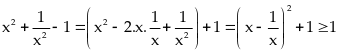
Nên
ta có:
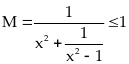 .
Dấu
.
Dấu
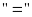 xảy
ra khi
xảy
ra khi
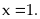
Vậy
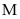 lớn
nhất là
lớn
nhất là
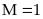 khi
khi
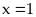
Bài
49: Cho
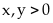 thỏa
mãn
thỏa
mãn
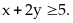 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
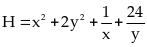
Lời giải
Ta
có:
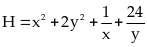
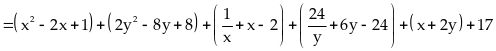
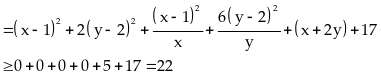
Dấu
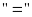 xảy
ra
xảy
ra
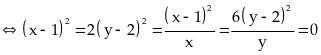 và
và
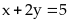
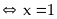 và
và
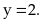 Vậy
Vậy
 nhỏ
nhất là
nhỏ
nhất là
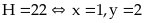
Bài
50:
Tìm giá trị nhỏ nhất của
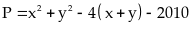
Lời giải
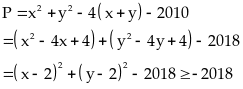
Vậy
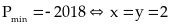
Bài
51: Cho
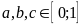 và
và
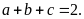 Tìm
giá trị lớn nhất của biểu thức
Tìm
giá trị lớn nhất của biểu thức
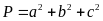
Lời giải
Vì
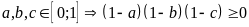
Ta
có:
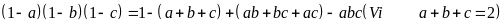
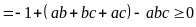

Lại
có:
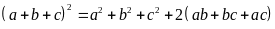
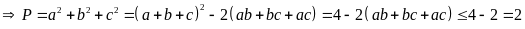
Vậy
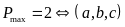 là
hoán vị của
là
hoán vị của
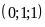
Bài
52: Tìm
giá trị nhỏ nhất của biểu thức sau:
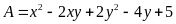
Tìm
giá trị lớn nhất của biểu thức sau:
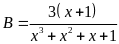
Lời giải
a) Ta có:
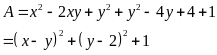
Do
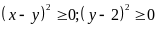
Nên
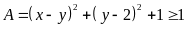
Dấu
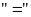 xảy
ra
xảy
ra
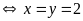
Vậy
GTNN của
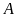 là
là
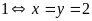
B)
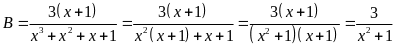
Do
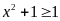 nên
nên
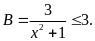 Dấu
Dấu
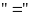 xảy
ra
xảy
ra
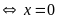
Vậy
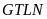 của
của
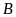 là
là
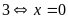
Bài
53: Tìm giá
trị nhỏ nhất của biểu thức:
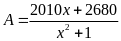
Lời giải
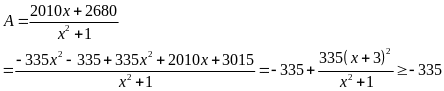
Vậy
giá trị nhỏ nhất của
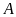 là
là
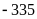 khi
khi
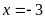
Bài
54: Tìm các
giá trị của
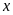 để biểu
thức:
để biểu
thức:
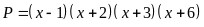 có
giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
có
giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Lời giải
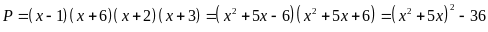
Ta
thấy
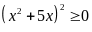 nên
nên
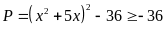
Do
dó
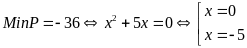
Bài
55: Tìm giá
trị nhỏ nhất của
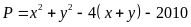
Lời giải
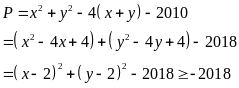
Vậy
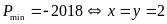
Bài
56: Tìm
giá trị nhỏ nhất của
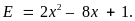
Lời giải
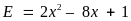
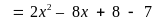
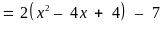
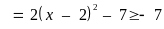
Vậy
giá trị nhỏ nhất của
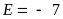 khi
khi
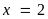
Bài
57: Tìm
giá trị nhỏ nhất của
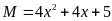
Lời giải
Ta
có :
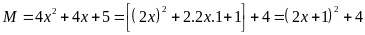
Vì
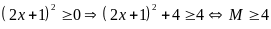
Vậy
GTNN của
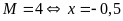
Bài
58:
Tìm
GTLN và GTNN của biểu thức:
![]() .
.
Lời giải:
HD: + Tìm GTLN:
Ta
có:
![]()
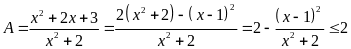
Dấu
“ =”
![]()
Suy
ra GTLN(A) = 2
![]() .
.
+ Tìm GTNN:
Ta
có:
![]()
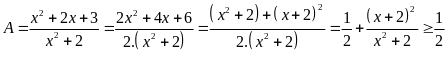
Dấu
“ =”
![]()
Suy
ra GTNN(A) =
![]()
![]()
Bài 59: Tìm giá trị của biến x để:
a)
![]() đạt giá trị lớn nhất b)
đạt giá trị lớn nhất b)
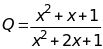 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất
Lời giải:
a)
![]() đạt giá trị lớn nhất.
đạt giá trị lớn nhất.
HD:
Ta có:
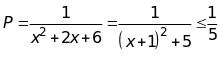 (
Vì 1 > 0 và
(
Vì 1 > 0 và
![]() )
)
Dấu
« = »
![]()
Suy
ra GTLN(P) =
![]()
![]() .
.
b)
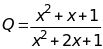 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất
HD:
ĐKXĐ:
![]()
Ta
có:
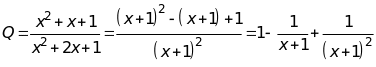
Đặt
![]() .
Ta có:
.
Ta có:
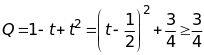
Dấu
« = »
![]()
Suy
ra GTNN(Q) =
![]()
![]()
Bài
60 :
a)
Tìm GTLN của
![]()
b)
Tìm GTNN của biểu thức
![]() , với
, với
![]()
Lời giải:
a)
Tìm GTLN của
![]()
Ta
có:
![]()
Đặt
![]() ,
khi đó:
,
khi đó:
![]()
Dấu
“=”
![]()
Suy
ra
![]()
b)Tìm
giá trị nhỏ nhất của biểu thức
![]() , với
, với
![]() .
.
Ta
có:
![]()
Dấu
“ =”
![]()
Vậy,
GTNN(B) =![]() .
.
Chú
ý: BĐT AM-GM cho 2 số
![]() không âm, ta có:
không âm, ta có:
![]() .
Dấu “=”
.
Dấu “=”![]()
*
Cách biến đổi B :
Ta viết
![]() .
.
Biến
đổi và đồng nhất thức hai vế, suy ra
![]() .
.
Bài 61: Tìm GTNN của:
a)
![]() ; b)
; b)
![]() ; c)
; c)
![]()
Lời giải:
Tìm GTNN của:
a)
Ta có:
![]()
(
Vì
![]() nên
nên
![]() ,
dùng BĐT Cô-si cho hai số dương
,
dùng BĐT Cô-si cho hai số dương
![]() và
và
![]() )
)
Dấu
« = »
![]()
Suy
ra
![]() .
.
b)
![]()
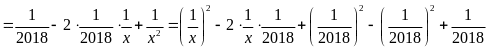
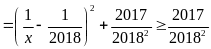
Dấu
“=”
![]() ( thỏa
( thỏa
![]() )
)
Suy
ra
![]()
![]()
c)
![]()
![]()
Dấu
“=”
![]() ( thỏa
( thỏa
![]() )
)
Suy
ra
![]() .
.
Bài
62:
Cho hai số x và y thoả mãn điều kiện:
![]()
a)
Tìm giá trị nhỏ nhất của biểu thức
![]() ;
;
b)
Tìm giá trị lớn nhất của biểu thức
![]()
Lời giải:
Tìm giá trị nhỏ nhất của biểu thức
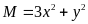
Từ
![]() ,
,
Khi
đó,
![]()
![]()
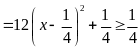
Dấu
“=”![]()
Suy
ra
![]()
Tìm giá trị lớn nhất của biểu thức
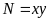
Từ
![]() ,
,
Khi
đó,
![]()
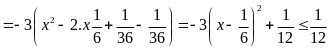
Dấu
« = »
![]()
Suy
ra
![]()
Bài
63: a)
Cho x, y là các số dương thoả mãn
![]() .
.
Tìm
giá trị nhỏ nhất của biểu thức
![]()
b)
Tìm GTLN của
![]()
Lời giải:
a)
Ta có :
![]()
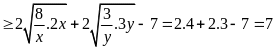
Dấu
“=”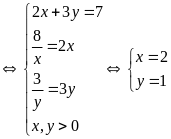
Suy
ra GTNN(Q) = 7![]() .
.
b)
Ta có:![]()
![]()
![]()
![]()
Dấu
“=”![]()
Suy
ra GTLN(A) = 1![]()
Bài
64: a)
Cho
![]() ,
tìm giá trị nhỏ nhất của biểu thức
,
tìm giá trị nhỏ nhất của biểu thức
![]()
b)
Tìm GTNN của
![]()
Lời giải:
a)
Ta có:
![]() ( Vì
( Vì
![]() )
)
![]() (
Vì
(
Vì
![]() )
)
![]()
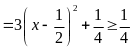
Dấu
“=”
![]()
Suy
ra
![]() .
.
b)
Tìm GTNN của
![]()
Ta
có:
![]()
![]()
![]()
Dấu
“=”
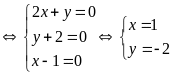
Suy
ra
![]() và
và
![]() .
.
Bài
65: a)
Tìm GTNN của![]() biết
biết
![]()
b)
Tìm GTNN của
![]()
c)
Tìm GTNN của
![]()
d)
Tìm GTLN của
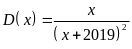 với
với
![]()
Lời giải:
a)
Tìm giá trị nhỏ nhất của:
![]() biết
biết
![]()
*
Cách 1 : Ta
có:
![]() +
+
![]() =
4
=
4
![]()
![]() +
2
+
2![]() +
+
![]() =
16 (1)
=
16 (1)
Ta
lại có:
![]()
![]()
![]() -
2
-
2![]() +
+
![]()
![]() 0
(2)
0
(2)
Từ
(1) và (2) suy ra 2![]() +
2
+
2![]()
![]() 16
16
![]()
![]() +
+
![]()
![]() 8
8
Vậy
giá trị nhỏ nhất của
![]()
*
Cách 2:
Ta có :
![]()
Suy
ra
![]()
Dấu
“=”
![]()
Vậy,
![]() .
.
b)
Ta có :
![]()
![]()
Dấu
“=”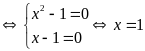
Suy
ra GTNN (B ) = 5![]()
c)
Ta có:
![]()
Đặt
![]() (
chú ý :
(
chú ý :
![]() )
)
Khi
đó,
![]()
Dấu
“=”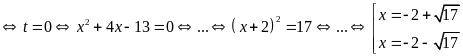
d)
Tìm giá trị của
![]() để biểu thức sau đạt GTLN:
để biểu thức sau đạt GTLN:
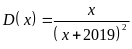 với
với
![]()
*Cách
1: Đặt
![]()
Khi
đó
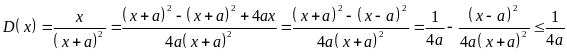
(
Vì
![]() ).
).
Dấu
“=”![]() .
.
Suy
ra
![]() .
.
*Cách
2: Đặt
![]()
Ta
có:
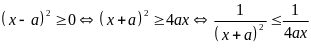 ( Vì
( Vì
![]() nên
nên
![]() )
)
Suy
ra
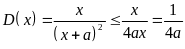 ( Vì
( Vì
![]() )
)
Dấu
“=”![]() .
.
Suy
ra
![]() .
.
Bài
66:
Tìm
giá trị nhỏ nhất của
![]() và các giá trị của
và các giá trị của
![]() tương ứng.
tương ứng.
Lời giải:
Tìm
giá trị nhỏ nhất của
![]() và các giá trị của
và các giá trị của
![]() tương ứng.
tương ứng.
Ta
biết:
![]() .
.
Đặt:
![]() .
.
Khi
đó biểu thức (*) viết thành:
![]() .
.
Dấu
“=” xảy ra
![]()
![]() .
.
*)
![]() .
.
*)
![]() .
.
Vậy
![]()
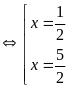
Bài
67: Cho
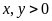 thỏa
mãn
thỏa
mãn
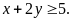 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
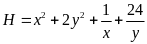 GTLN
GTLN
Lời giải
Ta
có:
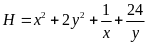
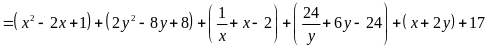
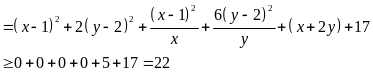
Dấu
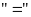 xảy
ra
xảy
ra
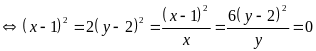 và
và
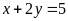
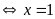 và
và
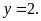 Vậy
Vậy
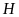 nhỏ
nhất là
nhỏ
nhất là
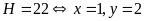
Bài
68: Cho hai
số không âm
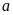 và
và
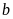 thỏa mãn:
thỏa mãn:
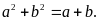 Tính
giá trị lớn nhất của biểu thức:
Tính
giá trị lớn nhất của biểu thức:
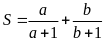
Lời giải
Ta
có:
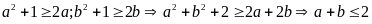
Chứng
minh được với hai số dương
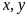 thì
thì
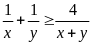
Do
đó:
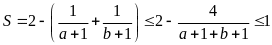
Vậy
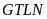 của
S là 1, dạt được khi
của
S là 1, dạt được khi
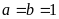
Bài
69: Cho hai
số dương
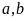 thỏa
mãn:
thỏa
mãn:
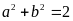
Tìm
giá trị nhỏ nhất của
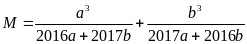
Lời giải
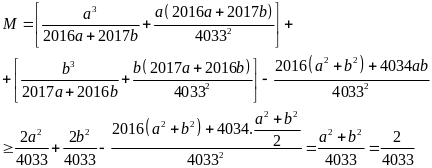
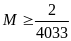 .
Dấu
.
Dấu
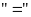 xảy
ra
xảy
ra
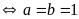
Vậy
GTNN của
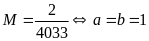
Bài
70: Cho
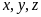 là
các số thực không âm. Tìm giá trị nhỏ nhất của
:
là
các số thực không âm. Tìm giá trị nhỏ nhất của
: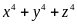 biết
biết
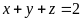
Lời giải
Áp dụng công thức Bunhiacopski ta có:
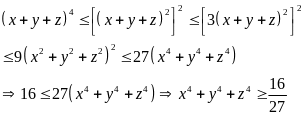
Vậy
GTNN của
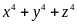 là
là
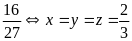
Bài
71: Tìm các
giá trị của
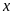 để
biểu thức:
để
biểu thức: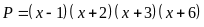 có
giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
có
giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Lời giải
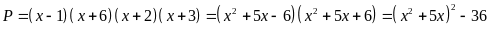
Ta
thấy
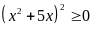 nên
nên
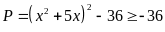
Do
dó
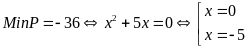
Bài
72: Tìm giá
trị nhỏ nhất của biểu thức
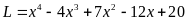
Lời giải
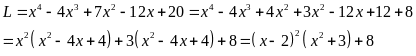
Do
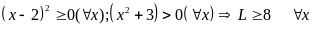
Đẳng
thức xảy ra
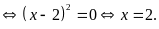 Vậy với
Vậy với
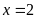 thì
L có giá trị nhỏ nhất.
thì
L có giá trị nhỏ nhất.
Giá trị nhỏ nhất của L là 8
Bài
73: Tìm giá
trị nhỏ nhất của biểu thức
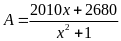 .
.
Lời giải
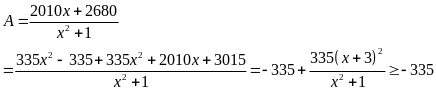
Vậy
GTNN của
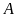 là
là
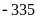 khi
khi
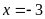
Bài 74: Tìm giá trị nhỏ nhất của biểu thức:
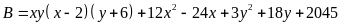
Lời giải
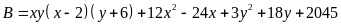
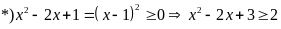 với
mọi
với
mọi

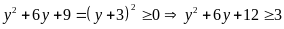 với
mọi
với
mọi
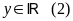
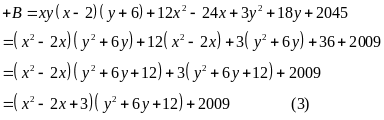
Từ
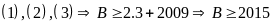
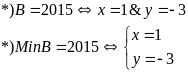
Bài
75: Cho
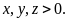 Tìm
giá trị nhỏ nhất của biểu thức :
Tìm
giá trị nhỏ nhất của biểu thức :
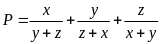
Lời giải
Đặt
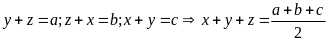
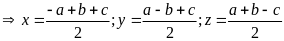
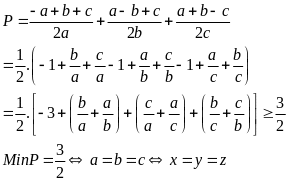
Bài
76:
Tìm
GTLN và GTNN của biểu thức:
![]() .
.
Lời giải
+ Tìm GTLN:
Ta
có:
![]()
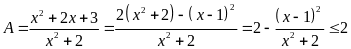
Dấu
“ =”
![]()
Suy
ra GTLN(A) = 2
![]() .
.
+ Tìm GTNN:
Ta
có:
![]()
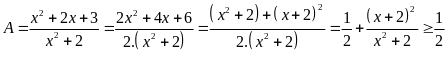
Dấu
“ =”
![]()
Suy
ra GTNN(A) =
![]()
![]()
Bài 77: Tìm giá trị của biến x để:
a)
![]() đạt giá trị lớn nhất b)
đạt giá trị lớn nhất b)
![]() đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất
Lời giải
a)
Ta
có:
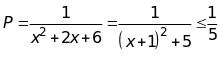 (
Vì 1 > 0 và
(
Vì 1 > 0 và
![]() )
)
Dấu
« = »
![]()
Suy
ra GTLN(P) =
![]()
![]() .
.
b)
ĐKXĐ:
![]()
Ta
có:
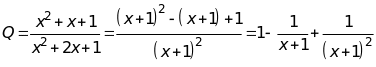
Đặt
![]() .
Ta có:
.
Ta có:
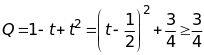
Dấu
« = »
![]()
Suy
ra GTNN(Q) =
![]()
![]()
Bài
78:
a) Tìm GTLN của
![]()
b)
Tìm GTNN của biểu thức
![]() , với
, với
![]()
Lời giải
a)
Tìm GTLN của
![]()
Ta
có:
![]()
Đặt
![]() ,
khi đó:
,
khi đó:
![]()
Dấu
“=”
![]()
Suy
ra
![]()
b)Tìm
giá trị nhỏ nhất của biểu thức
![]() , với
, với
![]() .
.
Ta
có:
![]()
Dấu
“ =”
![]()
Vậy,
GTNN(B) =![]() .
.
Bài 79: Tìm GTNN của:
a)
![]() ; b)
; b)
![]() ; c)
; c)
![]()
Lời giải
a)
Ta có:
![]()
(
Vì
![]() nên
nên
![]() ,
dùng BĐT Cô-si cho hai số dương
,
dùng BĐT Cô-si cho hai số dương
![]() và
và
![]() )
)
Dấu
« = »
![]()
Suy
ra
![]() .
.
b)Ta
có
![]()
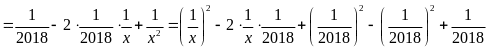
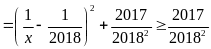
Dấu
“=”
![]() ( thỏa
( thỏa
![]() )
)
Suy
ra
![]()
![]()
c)
![]()
![]()
Dấu
“=”
![]() ( thỏa
( thỏa
![]() )
)
Suy
ra
![]() .
.
Bài
80:
Cho
hai số x và y thoả mãn điều kiện:
![]()
Tìm giá trị nhỏ nhất của biểu thức
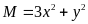 ;
;Tìm giá trị lớn nhất của biểu thức
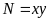
Lời giải
Tìm giá trị nhỏ nhất của biểu thức
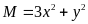
Từ
![]() ,
,
Khi
đó,
![]()
![]()
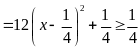
Dấu
“=”![]()
Suy
ra
![]()
Tìm giá trị lớn nhất của biểu thức
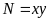
Từ
![]() ,
,
Khi
đó,
![]()
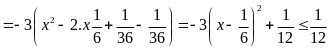
Dấu
« = »
![]()
Suy
ra
![]()
Bài
81:
a)
Cho x, y là các số dương thoả mãn
![]() .
Tìm giá trị nhỏ nhất của biểu thức
.
Tìm giá trị nhỏ nhất của biểu thức
![]()
Tìm GTLN của
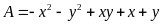
Lời giải
a)
Ta có :
![]()
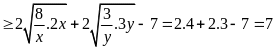
Dấu
“=”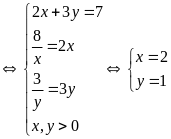
Suy
ra GTNN(Q) = 7![]() .
.
b)
Ta có:![]()
![]()
![]()
![]()
Dấu
“=”![]()
Suy
ra GTLN(A) = 1![]()
Bài
82:
a)
Tìm GTNN của![]() biết
biết
![]()
b)
Tìm GTNN của
![]()
c)
Tìm GTNN của
![]()
d)
Tìm GTLN của
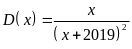 với
với
![]()
Lời giải
a)
*
Cách 1 : Ta
có:
![]() +
+
![]() =
4
=
4
![]()
![]() +
2
+
2![]() +
+
![]() =
16 (1)
=
16 (1)
Ta
lại có:
![]()
![]()
![]() -
2
-
2![]() +
+
![]()
![]() 0
(2)
0
(2)
Từ
(1) và (2) suy ra 2![]() +
2
+
2![]()
![]() 16
16
![]()
![]() +
+
![]()
![]() 8
8
Vậy
giá trị nhỏ nhất của
![]()
*
Cách 2:
Ta có :
![]()
Suy
ra
![]()
Dấu
“=”
![]()
Vậy,
![]() .
.
b)
Ta có :
![]()
![]()
Dấu
“=”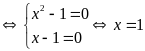
Suy
ra GTNN (B ) = 5![]()
c)
Ta có:
![]()
Đặt
![]() (
chú ý :
(
chú ý :
![]() )
)
Khi
đó,
![]()
Dấu
“=”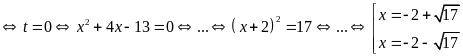
d)
Tìm giá trị của
![]() để biểu thức sau đạt GTLN:
để biểu thức sau đạt GTLN:
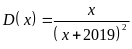 với
với
![]()
*Cách
1: Đặt
![]()
Khi
đó
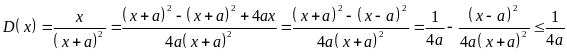
(
Vì
![]() ).
).
Dấu
“=”![]() .
.
Suy
ra
![]() .
.
*Cách
2: Đặt
![]()
Ta
có:
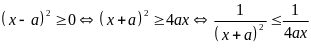 ( Vì
( Vì
![]() nên
nên
![]() )
)
Suy
ra
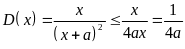 ( Vì
( Vì
![]() )
)
Dấu
“=”![]() .
.
Suy
ra
![]() .
.
Bài
83:
:
a) Cho
![]() ,
tìm giá trị nhỏ nhất của biểu thức
,
tìm giá trị nhỏ nhất của biểu thức
![]()
b)
Tìm GTNN của
![]()
Lời giải
a)
Ta có:
![]() ( Vì
( Vì
![]() )
)
![]() (
Vì
(
Vì
![]() )
)
![]()
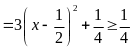
Dấu
“=”
![]()
Suy
ra
![]() .
.
b)
Tìm GTNN của
![]()
Ta
có:
![]()
![]()
![]()
Dấu
“=”
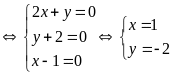
Suy
ra
![]() và
và
![]() .
.
Bài
84:
Tìm giá trị nhỏ nhất của
![]() và các giá trị của
và các giá trị của
![]() tương ứng.
tương ứng.
Lời giải
Ta
biết:
![]() .
.
Đặt:
![]() .
.
Khi
đó biểu thức (*) viết thành:
![]() .
.
Dấu
“=” xảy ra
![]()
![]() .
.
*)
![]() .
.
*)
![]() .
.
Vậy
![]()
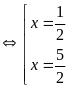
Bài
85:
Cho
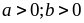 và
và
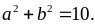 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
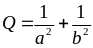
Lời giải
Ta có:
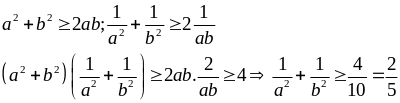
Vậy
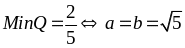
Bài
86: Tìm
giá trị nhỏ nhất của biểu thức
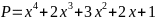
Lời giải
Ta
có:
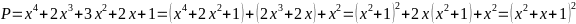
Vì
x2
+
x + 1 =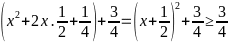
Suy
ra :
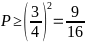
Dấu
bằng xảy ra khi và chỉ khi
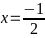
Bài 87: Cho hai số không âm a và b thỏa mãn: a2 + b2 = a + b. Tính giá trị lớn nhất của biểu thức:
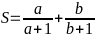
Lời giải
Ta
có:
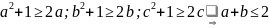
Chứng
minh được với hai số dương x,y thì
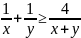
Do
đó:
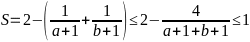
Vậy GTLN của S là 1, dạt được khi a = b = 1
Bài 88: Cho x,y,z là các số dương thỏa mãn x + y + z =1. Tìm giá trị nhỏ nhất của biểu thức :
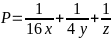
Lời giải
Ta có:
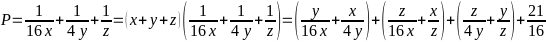
Theo
BĐT cô si ta có :
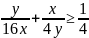 .
Dấu bằng xảy ra khi và chỉ khi y = 2x
.
Dấu bằng xảy ra khi và chỉ khi y = 2x
Tương
tự :
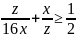 .
Dấu bằng xảy ra khi và chỉ khi z = 4x
.
Dấu bằng xảy ra khi và chỉ khi z = 4x
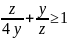 . Dấu bằng xảy ra khi và chỉ khi z = 2y
. Dấu bằng xảy ra khi và chỉ khi z = 2y
Suy
ra:
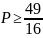 .
Dấu “=” xảy ra khi
.
Dấu “=” xảy ra khi
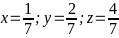
Vậy:
Min P =
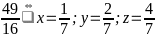
Bài
89: Tìm
giá trị nhỏ nhất của biểu thức :
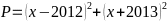
Lời giải
Ta có:
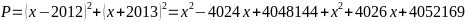

Vậy
Min P = 8100312,5
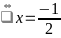
Bài
90: Tìm
giá trị nhỏ nhất của biểu thức
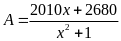
Lời giải
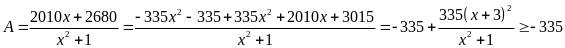
Vậy
giá trị nhỏ nhất của A là
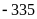 khi
khi
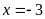
Bài
91: a. Tìm
giá trị lớn nhất của tổng x + y + z biết rằng x + 5y =
21 và 2x + 3z = 51 với x, y, z
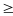 0
0
b.
Tìm giá trị nhỏ nhất, lớn nhất của các phân thức B
=
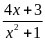
Lời giải
a) Cộng vế với vế của các đẳng thức x + 5y = 21 và 2x + 3z =51 ta được
3(x + y + z) + 2y = 72
Như
vậy 3(x + y + z) lớn nhất khi và chỉ khi 2y nhỏ nhất .
Mặt
khác y
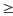 0 nên 2y nhỏ nhất khi y = 0
0 nên 2y nhỏ nhất khi y = 0
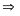 x = 21 và z = 3
x = 21 và z = 3
Do
đó 3(x + y + z) lớn nhất bằng 72
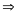 x + y + z lớn nhất bằng 24 khi x = 21; y = 0 và z = 3
x + y + z lớn nhất bằng 24 khi x = 21; y = 0 và z = 3
b)
Ta có
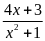 =
=
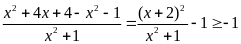
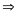 minB = -1 với x = -2
minB = -1 với x = -2
Vậy giá trị nhỏ nhất của B là B = -1 khi x = -2
Mặt
khác ta lại có
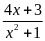 =
=
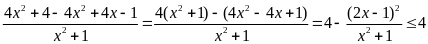
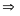 maxB
= 4 với x =
maxB
= 4 với x =
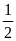
Vậy
giá trị lớn nhất của B là B = 4 khi x =
Bài
92: Tìm
giá trị nhỏ nhất của biểu thức
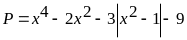 .
.
Lời giải
Ta
có
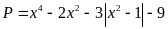 =
=
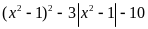
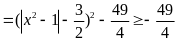
Đẳng
thức xảy ra khi
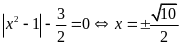
Vậy
Min P =
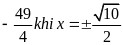
Bài
93: Tìm
giá trị lớn nhất của biểu thức
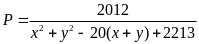
Lời giải
Ta
có
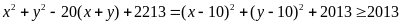 với mọi x, y.
với mọi x, y.
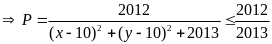
P
=
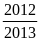 khi x = 10 và y = 10
khi x = 10 và y = 10
Vậy
Max P
=
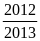 khi x = 10 và y = 10.
khi x = 10 và y = 10.
Bài
94: Cho
các số a, b,c thỏa mãn a + b + c =
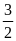 .
Tìm giá trị nhỏ nhất của biểu thức
P = a2
+ b2
+ c2
.
Tìm giá trị nhỏ nhất của biểu thức
P = a2
+ b2
+ c2
Lời giải
Ta
có:
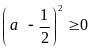 với mọi a
với mọi a
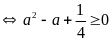 với
mọi a
với
mọi a
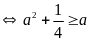 với
mọi a (1)
với
mọi a (1)
Tương
tự:
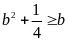 với mọi b (2)
với mọi b (2)
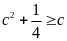 với
mọi c (3)
với
mọi c (3)
Cộng vế với vế của (1), (2) và (3) ta được :
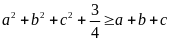 .
.
Vì
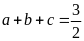 nên: P =
nên: P =
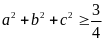
Dấu
“=” xảy ra khi a = b = c =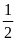 .
.
Vậy
giá trị nhỏ nhất của biểu thức P là
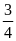 đạt
được khi và chỉ khi a = b = c =
đạt
được khi và chỉ khi a = b = c =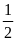 .
.
Bài
95: Cho
hai số dương
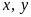 có
tổng bằng 1. Tìm giá trị nhỏ nhất của biểu thức:
có
tổng bằng 1. Tìm giá trị nhỏ nhất của biểu thức:
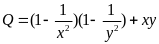
Lời giải
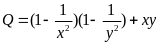
=
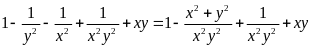
=
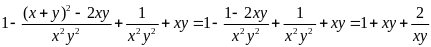
Áp
dụng BĐT AM-GM ta có
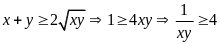 (*)
(*)
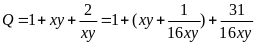
Áp dụng BĐT AM-GM và kết hợp (*) ta có:
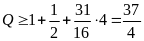
Đẳng
thức xảy ra
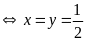 .
Vậy
.
Vậy
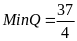 khi
khi
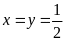 .
.
Bài 96:
Tìm
giá trị nhỏ nhất của biểu thức
![]() ,
trong đó x,
y
là các số thực thoả mãn điều kiện:
,
trong đó x,
y
là các số thực thoả mãn điều kiện:
![]() .
.
Lời giải
Tìm
giá trị nhỏ nhất của biểu thức
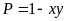 ,
trong đó x,
y
là các số thực thoả mãn điều kiện:
,
trong đó x,
y
là các số thực thoả mãn điều kiện:
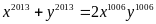 .
.
Ta
có:
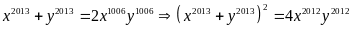 (2)
(2)
Mặt
khác:
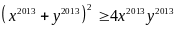 (3)
(3)
Từ
(2) và (3) suy ra:
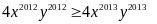
Hay
:
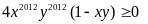 .Do
đó
.Do
đó
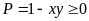 .
.
Đẳng
thức xảy ra khi:
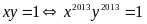 (4).
(4).
Từ
(1) và (4) ta có:
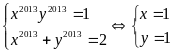 .
.
Vậy Min (P) = 0 khi x = y =1.
Bài 97:
a)
Cho
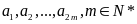 thoả mãn
thoả mãn
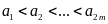 .
.
Tìm
GTNN của biểu thức
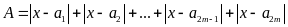 .
.
b)
Cho
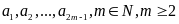 thoả mãn
thoả mãn
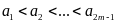 .
.
Tìm
GTNN của biểu thức
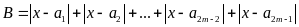 .
.
Lời giải
a)
Ta có:
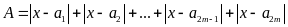
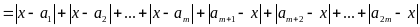
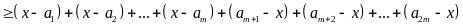
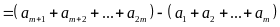
Dấu
“=”
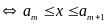 .
.
Vậy,
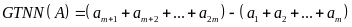 .
Dấu
“=”
.
Dấu
“=”
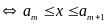 .
.
b)
Ta có: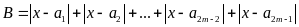
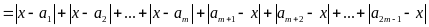
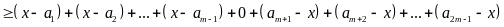
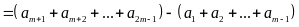
Dấu
“=”
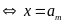 .
.
Vậy,
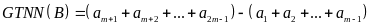 .
Dấu “=”
.
Dấu “=”
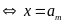 .
.
Bài
98: Cho
m,
n
là các số thực thay đổi sao cho
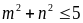 .
Hãy tìm giá trị nhỏ nhất của biểu thức:
.
Hãy tìm giá trị nhỏ nhất của biểu thức: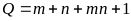 .
.
Lời giải
Cho
m,
n
là các số thực thay đổi sao cho
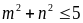 (1). Hãy tìm giá trị nhỏ nhất của biểu thức:
(1). Hãy tìm giá trị nhỏ nhất của biểu thức: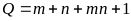 (2).
(2).
Từ
(2) ta có:
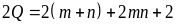
Do
đó:
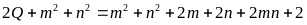
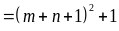
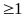
Suy
ra: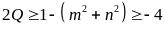 (do (1))
(do (1))
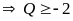 .
.
Dấu
“=” xảy ra
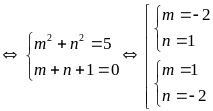 .
.
Vậy Min Q = -2 khi m =-2, n =1 hoặc m =1, n = -2.
Bài 99:
Tìm
giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
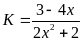
Lời giải
Ta
có:
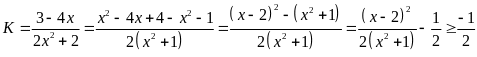
Dấu
“=”
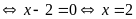
Suy
ra
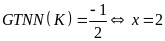
Ta
có:

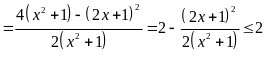
Dấu
“=”
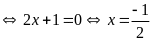
Suy
ra
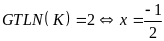
Bài 100:
Cho
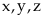 là
các số thực dương thỏa mãn:
là
các số thực dương thỏa mãn:
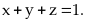
Tìm
giá trị nhỏ nhất của biểu thức:
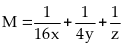
Lời giải
Vì
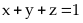 nên:
nên:
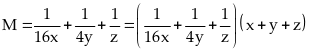
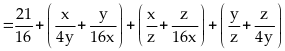
Ta
có:
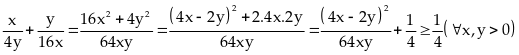
Tương
tự:
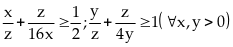
Từ
đó
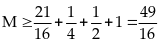 .
Dấu
.
Dấu
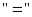 xảy
ra
xảy
ra
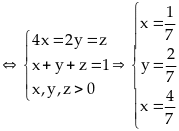
Vậy
GTNN của
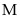 là
là
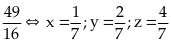
Bài
101:
Cho
các số thực dương
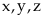 thỏa
mãn
thỏa
mãn
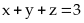
Tìm
giá trị nhỏ nhất của biểu thức
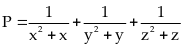
Lời giải
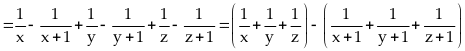
Áp
dụng BĐT
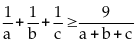 và
và
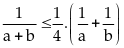 với
với
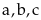 dương,
dấu bằng xảy ra
dương,
dấu bằng xảy ra
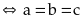
Ta
có:
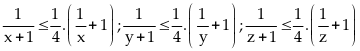
Bởi vậy :
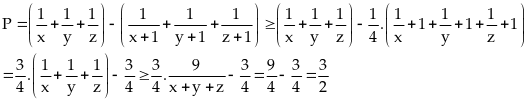
Vậy
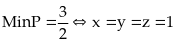
Bài
102:
Cho
hai số
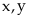 thỏa
mãn điều kiện
thỏa
mãn điều kiện
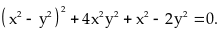 Tìm
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
Tìm
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
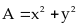
Lời giải
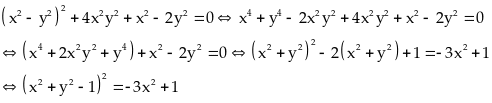
Ta
có:
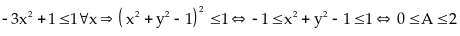
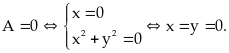 Vậy
Vậy
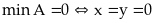
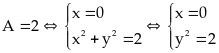 .
Vậy
.
Vậy
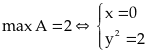
Bài
103:
Tìm
giá trị nhỏ nhất của
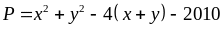
Lời gải
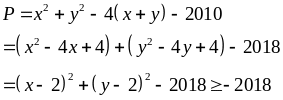
Vậy
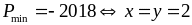
Bài
104: Cho
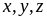 là
các số dương thỏa mãn
là
các số dương thỏa mãn
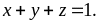
Lời gải
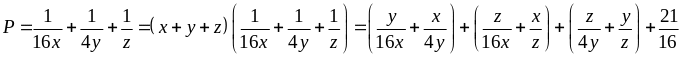 Theo
BĐT cô si ta có:
Theo
BĐT cô si ta có:
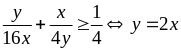
Tương
tự
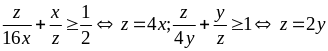
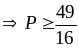 .
Dấu bằng xảy ra khi
.
Dấu bằng xảy ra khi
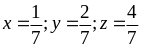
Bài
105:
Cho
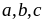 là
3 số dương thỏa mãn:
là
3 số dương thỏa mãn:
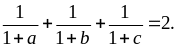 Tìm
giá trị lớn nhất của biểu thức
Tìm
giá trị lớn nhất của biểu thức
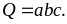
Lời gải
Ta
có:
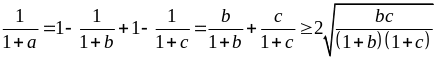
Tương
tự:
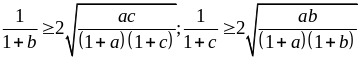
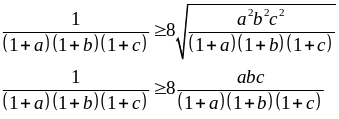
Dấu
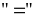 xảy
ra
xảy
ra
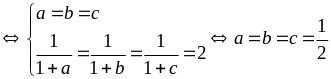
Bài
106:
Cho
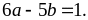 Tìm
giá trị nhỏ nhất của
Tìm
giá trị nhỏ nhất của
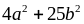
Lời gải
Đặt
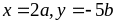 .
Áp dụng bất đẳng thức Bunhiacopxki ta có:
.
Áp dụng bất đẳng thức Bunhiacopxki ta có:
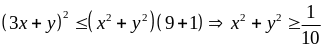 hay
hay
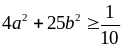 Dấu bằng xảy ra
Dấu bằng xảy ra
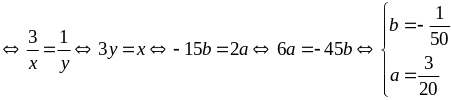
Bài
107: Tìm
giá trị nhỏ nhất của biểu thức
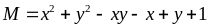
Lời giải
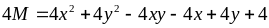
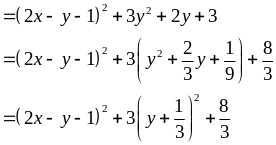
Giá
trị nhỏ nhất của
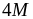 là
là
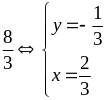
Nên
giá trị nhỏ nhất của
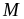 là
là
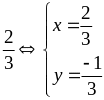
Bài
108: Cho
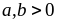 và
và
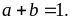 Tìm
giá trị nhỏ nhất của biểu thức:
Tìm
giá trị nhỏ nhất của biểu thức:
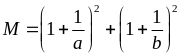
Lời giải
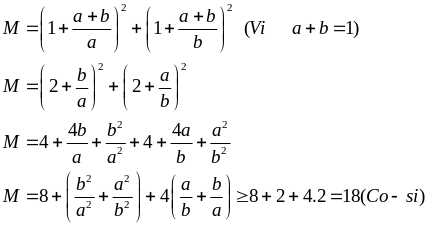
Dấu
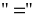 xảy
ra
xảy
ra
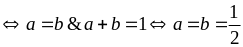
Vậy
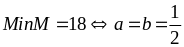
Bài 109:
Tìm giá trị nhỏ nhất của biểu thức sau:
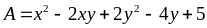
Tìm giá trị lớn nhất của biểu thức sau:
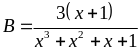
Tìm giá trị nhỏ nhất của biểu thức
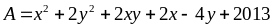
Lời giải
Ta có:
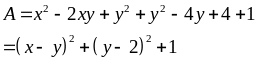
Do
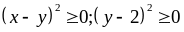
Nên
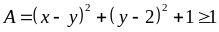
Dấu
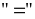 xảy
ra
xảy
ra
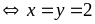
Vậy
GTNN của
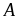 là
là
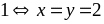
Do
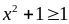 nên
nên
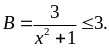 Dấu
Dấu
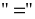 xảy
ra
xảy
ra
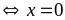
Vậy
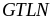 của
của
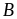 là
là
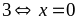
Ta có:
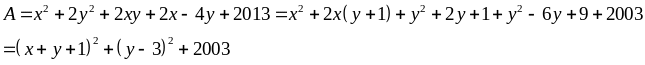 Nhận
thấy với mọi
Nhận
thấy với mọi
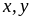 ta
có:
ta
có:
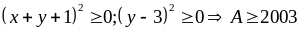
Dấu
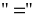 xảy
ra khi
xảy
ra khi
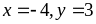
Vậy
Giá trị nhỏ nhất của
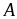 là
là
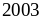 đạt
được khi
đạt
được khi
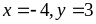
Bài 110: Tìm giá trị nhỏ nhất của biểu thức
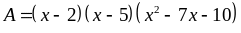
Lời giải
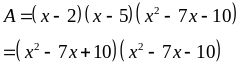
Đặt
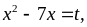 ta
có biểu thức:
ta
có biểu thức:
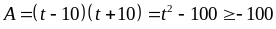
Dấu
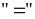 xảy
ra
xảy
ra
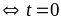
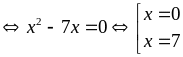
Với
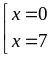 thì
thì
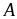 đạt
giá trị nhỏ nhất bằng
đạt
giá trị nhỏ nhất bằng
Kết thúc phần Ôn Thi HSG Đại Số 8 về Giá Trị Lớn Nhất và Nhỏ Nhất có Lời Giải Chi Tiết, chúng ta đã hoàn thành một giai đoạn quan trọng trong quá trình ôn tập và chuẩn bị cho kỳ thi Học Sinh Giỏi môn Đại Số. Phần này đã giúp chúng ta rèn luyện kỹ năng tìm giá trị lớn nhất và nhỏ nhất của biểu thức, một trong những nội dung quan trọng trong chương trình học môn Toán.
Ngoài Giá Trị Lớn Nhất Nhỏ Nhất Ôn Thi HSG Đại Số 8 Có Lời Giải Chi Tiết thì các tài liệu học tập trong chương trình 8 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm