Định lý Pytago trong tam giác vuông là gì và những dạng bài cơ bản

Định lý Pitago là một kiến ​​thức vô cùng quan trọng, đặt nền tảng cho các em giải các bài tập phức tạp sau này. Vì vậy, hãy tập trung học và ghi chép cẩn thận. Hôm nay, các em sẽ cùng trangtailieu.com tìm hiểu định lý Pitago và cách tính các cạnh còn lại của tam giác vuông khi biết số đo 2 cạnh của tam giác vuông.

Lý thuyết cần nhớ bài Định lý pytago

Định lý pytago là gì?

Định lý Pytago (hay còn gọi là định lý Pythagoras theo tiếng Anh) là một liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Định lý pytago thuận phát biểu rằng trong 1 tam giác vuông: Bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc vuông.

Định lý có thể viết thành một phương trình liên hệ giữa độ dài của các cạnh là a, b và c, thường gọi là công thức Pytago: ΔABC vuông tại A thì ta có:

BC2 = AB2 + AC2

Ví dụ bài tập:

Cho tam giác ABC vuông tại A có AB= 6cm, AC= 8cm. Tính BC

Áp dụng định lý Pitago trong tam giác vuông ABC, ta có: BC2=AB2+AC2

Nên BC2=62+82=36+64=100

Vậy BC=10 cm

Chú ý: Dựa vào định  Pytago, khi ta biết độ dài 2 cạnh của tam giác vuông, ta sẽ tính được độ dài cạnh còn lại

Cách chứng minh định lý pitago lớp 7

Ta có thể chứng minh định lý Pitago đơn giản qua hình dưới đây:

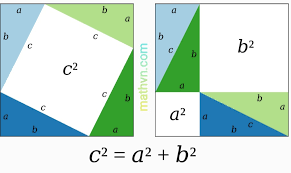
Cách chứng minh định lý pitago

Ở hình trên ta có 2 hình vuông lớn có diện tích bằng nhau là: (a+b)2. Trong mỗi hình lại có 4 tam giác vuông bằng nhau có diện bằng nhau là 1/2(a.b). Do đó diện tích khoảng trắng của 2 hình sẽ bằng nhau. Như vậy, diện tích của hình vuông c sẽ bằng tổng diện tích của 2 hình vuông a và b nên ta có: C2 = A2 + B2

Chứng minh định lý Pytago đảo

Định nghĩa: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông. Định lý Pytago đảo được sử dụng rất phổ biến cũng như gồm nhiều ứng dụng trong thực tiễn. 

>>> Mẹo ghi nhớ:

+Trong tam giác vuông, bình phương cạnh huyền bằng bình phương các cạnh góc vuông

+Ngược lại, nếu 1 tam giác có một cạnh bằng bình phương 2 cạnh còn lại thì đó là tam giác vuông, cạnh đó được gọi là cạnh huyền

Bài tập ứng dụng Định lý Pitago

Bài tập 1:

Xét tam giác ABC vuông tại A, cho bảng sau, tính chiều dài cạnh huyền BC.

AB	3	5	11	9	18	6	7
AC	4	7	6	17	6	12	4
BC	?	?	?	?	?	?	?

Lời giải:

Vì tam giác ABC vuông tại A, theo định lý Pytago ta có:

BC2 = AC2 + AB2 

=> BC = √(AC2 + BC2)

AB	3	5	11	9	18	6	7
AC	4	7	6	17	6	12	4
BC	5	8,6	12,5	19,2	19	13	8,1

Bài tập 2:

Xét tam giác ABC vuông tại A:

1. Biết chiều dài cạnh AB = 4 cm, chiều dài cạnh BC = 6 cm, tính chiều dài cạnh AC
2. Biết chiều dài cạnh AC = 2 cm, chiều dài cạnh BC = 7 cm, tính chiều dài cạnh AB
3. Biết chiều dài cạnh AB = 3 cm, chiều dài cạnh AC = 5 cm, tính chiều dài cạnh BC

Lời giải

1. Ta có: BC² = AC² + AB² 

=> AC² = BC² – AB² 

=> AC² = 6² – 4² 

=> AC = √20

Vậy chiều dài của cạnh AC là √20 cm

2. Ta có BC² = AC² + AB² 

=> AB² = BC² – AC² 

=> AB² = 7² – 2 ²

=> AB = √45

Vậy chiều dài cạnh AB = √45 cm

3. Ta có: BC² = AC² + AB² 

=> BC² = 3² + 5²

=> BC = √34

Vậy chiều dài cạnh BC là√34

Bài tập 3:

Tính chiều dài cạnh huyền của các tam giác sau, biết:

1. Tam giác MNO vuông tại M có cạnh MO = 4 cm, cạnh MN = 5 cm
2. Tam giác PQR vuông tại P có cạnh PQ = 7 cm, cạnh PR = 6 cm
3. Tam giác BCD vuông tại B có cạnh BC = 8 cm, cạnh BD = 2 cm
4. Tam giác IKL vuông tại I có cạnh IL = 4,5 cm, cạnh IK = 8 cm

Lời giải:

1. Vì tam giác MNO vuông tại M, NO là cạnh góc vuông, do đó, ta áp dụng định lý Pytago trong tam giác vuông:

NO2 = MN2 + MO2

=> NO2 = 42 + 52

=> NO2 = 41

=> NO = √41

=> NO = 6,4

Vậy chiều dài cạnh NO của tam giác MNO là 6,4 cm

1. Vì tam giác PQR vuông tại P, QR là cạnh góc vuông, do đó, ta áp dụng định lý Pytago trong tam giác vuông:

QR2 = PQ2 + PR2

=> QR2 = 72 + 62

=> QR2 = 85

=> QR = √85

=> QR = 9,2

Vậy chiều dài cạnh QR của tam giác PQR là 9,2 cm

1. Vì tam giác BCD vuông tại B, CD là cạnh góc vuông, do đó, ta áp dụng định lý Pytago trong tam giác vuông:

CD2 = BC2 + BD2

=> CD2 = 82 + 22

=> CD2 = 70

=> CD = √70

=> CD = 8,4

Vậy chiều dài cạnh CD của tam giác BCD là 8,4 cm

1. Vì tam giác IKL vuông tại I, KL là cạnh góc vuông, do đó, ta áp dụng định lý Pytago trong tam giác vuông:

KL2 = IL2 + IK2

=> KL2 = 4,52 + 82

=> KL2 = 84,25

=>KL = √84,25

=> KL = 9,2

Vậy chiều dài cạnh CD của tam giác BCD là 9,2 cm

Bài 53 sách giáo khoa:

1. Vì x là cạnh huyền của tam giác, áp dụng định lý Pytago ta có

x² = 12² + 5²

=> x² = 169

=> x = 13

Vậy chiều dài của x là 13

1. Vì x là cạnh huyền của tam giác, áp dụng định lý pytago ta có

x² = 1² + 2 ² 

=> x² = 5

=> x = √5 = 2,34

Vậy chiều dài của x là 2,34

1. Vì x là cạnh góc vuông, áp dụng định lý Pytago ta có

29² = x² + 21²

=> x²  = 29² – 21²

=> x²  = 841 – 441

=> x² = 400

=> x = 20

Vậy chiều dài của x là 20

1. Vì x là cạnh góc vuông, áp dụng định lý Pytago ta có:

=> x²  = √7² + 3²

=> x²  = 7 + 9

=> x = 4

Vậy chiều dài của x là 4

Hi vọng nội dung khóa học của Trang Tài Liệu có thể giúp các em nắm vững kiến ​​thức về Định lý Pitago. Đặc biệt, để tiếp thu kiến ​​thức của bài học này một cách hiệu quả, các em học sinh nên củng cố lại kiến ​​thức đã học bằng cách ôn tập và giải bài tập về tam giác vuông. Hoặc các bạn có thể tham khảo trọn bộ khóa học nâng cao để làm quen với các dạng câu hỏi và đạt điểm cao trong kỳ thi. Theo dõi Trang Tài Liệu thường xuyên để cập nhật các khóa học bổ ích.