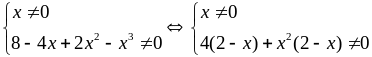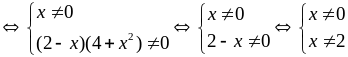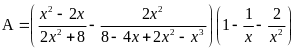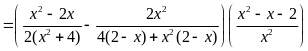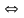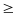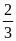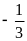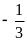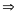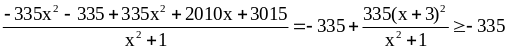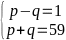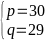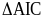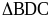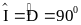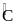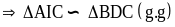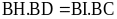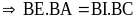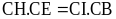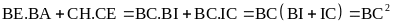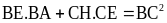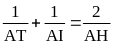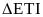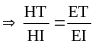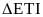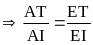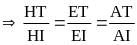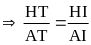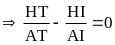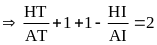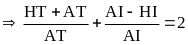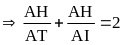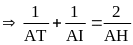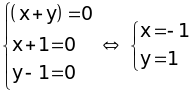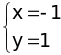Đề Thi HSG Toán 8 THCS Gia Trấn 2022 có đáp án
Đề Thi HSG Toán 8 THCS Gia Trấn 2022 Có Đáp Án – Toán 8 được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
ĐỌC THÊM
Trong bài viết hôm nay, chúng ta sẽ cùng tìm hiểu về Đề Thi HSG (Học sinh giỏi) môn Toán lớp 8 tại Trường THCS Gia Trấn năm 2022. Đây là một bộ đề thi đặc biệt dành cho những học sinh có khả năng xuất sắc và đam mê Toán học.
Bộ đề thi này bao gồm một loạt câu hỏi và bài tập Toán học đòi hỏi sự tư duy sắc bén, khả năng giải quyết vấn đề và kỹ năng tính toán chính xác. Các câu hỏi và bài tập được lựa chọn một cách kỹ lưỡng để thách thức tối đa khả năng hiểu biết và ứng dụng kiến thức của các em học sinh.
Đề thi HSG Toán 8 THCS Gia Trấn 2022 không chỉ kiểm tra khả năng giải quyết bài toán, mà còn đánh giá sự hiểu biết sâu sắc về các khái niệm, quy tắc và phương pháp trong môn Toán học. Nó là một cơ hội để các em thể hiện khả năng và tiềm năng của mình trong lĩnh vực này.
Đáp án chi tiết kèm theo đề thi sẽ giúp các em học sinh tự kiểm tra và đánh giá năng lực của mình. Nó cũng là một công cụ hữu ích để làm rõ các phương pháp và quy trình giải quyết bài toán, từ đó nâng cao khả năng giải quyết vấn đề và cải thiện kỹ năng Toán học của mỗi học sinh.
Qua đề thi HSG Toán 8 THCS Gia Trấn 2022, các em học sinh sẽ có cơ hội rèn luyện và nâng cao khả năng toán học của mình. Hãy dành thời gian làm bài, tìm hiểu từng câu hỏi và bài tập, và sử dụng đáp án chi tiết để tự đánh giá và cải thiện năng lực của mình.
Hãy sẵn sàng đối mặt với những thử thách và khám phá những giải pháp sáng tạo trong môn Toán học. Mời các em cùng khám phá và trải nghiệm Đề Thi HSG Toán 8 THCS Gia Trấn 2022 để phát triển khả năng và đạt được thành tích cao trong lĩ
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
TRƯỜNG THCS GIA TRẤN
|
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 8 Năm 2022 MÔN: TOÁN Thời gian làm bài: 150 phút. (Đề thi gồm 05 câu, 01 trang) |
Câu 1 (4,0 điểm):
Phân tích đa thức thành nhân tử:
6x2 – 5x +1
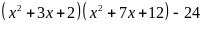
Cho biểu thức:
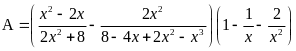 .
.
a) Tìm x để giá trị của A được xác định. Rút gọn biểu thức A.
b) Tìm giá trị nguyên của x để A nhận giá trị nguyên.
Câu 2 (3,5 điểm):
1. Giải các phương trình:
a) 4x – 12.2x + 32 = 0
b)
![]()
2.Tìm giá trị nhỏ nhất của biểu thức: A = 13x2 + y2 + 4xy – 2y – 16x + 2026
Câu 3 (4,0 điểm)
1. Cho đa thức bậc hai P(x)=ax2+bx+c.Tìm a; b; c biết P(0)=37; P(1)=14; P(2)=2011
2.
Tìm giá trị nhỏ nhất của biểu thức
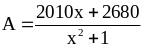 .
.
3, Tìm số tự nhiên n để n-18 và n +41 là hai số chính phương?
Câu
4
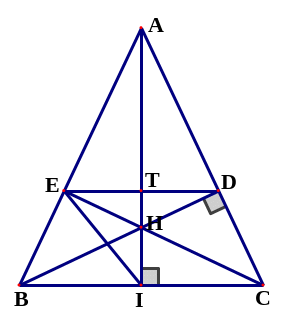
(6,0 điểm). Cho
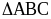 cân tại A, hai đường cao AI và BD cắt nhau tại H.
cân tại A, hai đường cao AI và BD cắt nhau tại H.
a) Chứng minh: Tam giác AIC đồng dạng với tam giác BDC
b)
Gọi E giao điểm của CH và AB. Chứng minh:
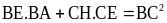
c)
Gọi T là giao điểm của DE và AH. Chứng minh:
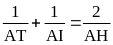
Câu 5 (2,0 điểm).
Tìm các cặp số nguyên x, y thỏa mãn:
5x2 + 5y2 + 8xy + 2x - 2y + 2 = 0
Chứng minh rằng: 8351634 + 8241142 chia hết cho 26
---------- Hết ----------
|
HƯỚNG DẪN CHẤM ĐỀ THI HỌC SINH GIỎI LỚP 8 Năm 2022 MÔN: TOÁN (Hướng dẫn chấm gồm 05 trang) |
I. Hướng dẫn chung
1. Bài làm của học sinh đúng đến đâu cho điểm đến đó.
2. Học sinh có thể sử dụng kết quả câu trước để làm câu sau.
3. Với bài hình, nếu hình vẽ sai hoặc không vẽ hình thì không chấm. Lời giải không khớp với hình vẽ thì không cho điểm.
4. Học sinh làm bài không theo cách nêu trong đáp án mà đúng thì cho đủ điểm thành phần như hướng dẫn.
II. Hướng dẫn chi tiết:
Câu |
Đáp án |
Điểm |
1 (4,0 điểm) |
1. ( 2 điểm): Mỗi ý đúng 1 điểm a. 6x2 – 5x +1 = 6x2 – 3x -2x +1 =3x(2x - 1) -(2x - 1) = (3x - 1)(2x - 1) |
0,5 0,25 0,25 |
b. = (x+1)(x+2)(x+3)(x+4)-24 = (x+1)(x+4)(x+2)(x+3) -24 = (x2+5x+4)(x2+5x+6)-24 Đặt x2+5x+4=a ta có: a(a+2)-24 =a2+2a-24=(a+6)(a-4) =(x2 +5x+12)(x2+5x-2) |
0.25
0,25
0,25 0,25 |
|
2.a. ( 1,5 điểm) +
A
xác định
Vậy
ĐKXĐ
:
+ Rút gọn A: |
0,5 |
|
|
|
|
b. ( 0,5 điểm)Tìm giá trị nguyên của x để A nhận giá trị nguyên. *
2
* Ta thấy x = 1 hoặc x = -1 (TMĐKXĐ) Vậy
A=
|
0,25
0,25
0,25
0,25
0,25
0,25 |
|
2 (3,5 điểm) |
1) ý a 1,0 điểm; ý b 1,5 điểm
a)
4x
– 12.2x
+32 = 0
HS lập bảng để phân ra các trường hợp *
Với x < 0 phương trình đã cho trở thành: - 2x + 4 =
4
*
Với
* Với 1 < x < 2 phương trình đã cho trở thành : -4x
+ 8 = 4
*
Với
Vậy
nghiệm của phương trình là các giá trị x thoả mãn
x =4;
2 , ( 1điểm) A = 13x2 + y2 + 4xy - 2y - 16x + 2026 = y2 + 4xy - 2y + 13x2 - 16x + 2026 = y2 + 2y(2x - 1) + (2x -1)2 + 9x2 - 12 x + 4+2022 = (y + 2x - 1)2 + (3x - 2)2 + 2022 Chứng
tỏ A
Vậy
giá trị nhỏ nhất của A = 2022 khi x =
|
0,25 0,25 0,25 0,25
0,25
0,25
0,5
0,25
0,25
0,25
0,25
0,25 0,25 0,25
0,25 |
3 (4,0 điểm) |
1.( 1.5 điểm) P(x)=ax2 + bx + c P(0)=
37
P(1)
= 14
P(2)
= 2011
Từ
(1) và (2)
|
0.25 0.25 0,25 0,25 0,5 |
2, (1 điểm)
=
Vậy giá trị nhỏ nhất của A là – 335 khi x = – 3 |
0,25
0,25
0,25 0,25 |
|
3.( 1.5 điểm) Để n+18 và n-41 là hai số chính phương thì n +18 = p2, n – 41 = q2 (p,q ϵ N) → p2 – q2 = 59 =1.59 (p-q)(p+q) = 1.59 Từ p = 30 → n+18=302 =900 n = 882 Với n= 882 → n – 41 = 841= 292 Vậy n=882 là số tự nhiên cần tìm |
0,25
0,25
0,25
0,25
0,25 |
|
4 (6,0 điểm) |
- Vẽ hình đúng để làm được ý a
|
0,25
|
a) (0,75 điểm) Xét
|
|
|
|
0,25 |
|
|
0,25 |
|
|
0,25 |
|
b) (2,5 điểm) -
Chứng minh được:
|
0,5 |
|
|
0,5 |
|
|
0,25 |
|
-
Chứng minh được:
|
0,5 |
|
|
0,5 |
|
Vậy
|
0,25 |
|
c) (2,5 điểm) Gọi
T là giao điểm của DE và AH. Chứng minh:
|
|
|
-
Chứng minh được
|
0,5 |
|
-
Chứng minh được EA là phân giác trong, ngoài của
|
0,25 |
|
|
0,25 |
|
|
0,25 |
|
|
0,25 |
|
|
0,25 |
|
|
0,25 |
|
|
|
|
|
0,25 |
|
|
0,25 |
|
5 (2,0 điểm) |
1, ( 1 điểm) 5x2 + 5y2 + 8xy + 2x - 2y + 2 = 0 (4x2 + 8xy + 4y2) + (x2+ 2x + 1) + (y2 - 2y + 1) = 0 4 (x + y)2 + (x + 1)2 + (y - 1)2 = 0 Vì 4 (x + y)2 0 ; (x + 1)2 0 ; (y - 1)2 0 với mọi giá trị x, y Nên 4 (x + y)2 + (x + 1)2 + (y - 1)2 0 với x, y. 4 (x + y)2 + (x + 1)2 + (y - 1)2 = 0 Vậy
|
0,25
0,25
0,25
0,25
|
2, ( 1 điểm) 8351 là số lẻ 8351634 là số lẻ 8241 là số lẻ 8241142 là số lẻ Do
đó: 8351634
+
8241142
là số chẵn
(8351634
+ 8241142)
Mặt
khác: (83512
+ 1)
Áp
dụng: (an
- bn)
8351634 + 8241142 = [(83512)317 - (-1)317] + [8241142 - (-1)142] Chia
hết cho 13 vì [(83512)317
- (-1)317]
và
[8241142
- (-1)142]
2 và 13 là số nguyên tố cùng nhau, 2. 13 = 26 Do đó 8351634 + 8241142 chia hết cho 26 |
0,25
0,25
0,25
0,25
|
|
|
|
---------------Hết---------------
Ngoài Đề Thi HSG Toán 8 THCS Gia Trấn 2022 Có Đáp Án – Toán 8 thì các đề thi trong chương trình lớp 8 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.