20 Đề Thi HSG Toán 8 Có Lời Giải
20 Đề Thi HSG Toán 8 Có Lời Giải được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
Trong cuộc hành trình khám phá vẻ đẹp của toán học, việc ôn tập và thử sức qua các đề thi HSG Toán 8 là một phần quan trọng để nắm vững kiến thức và rèn luyện kỹ năng giải quyết vấn đề. Tuy nhiên, tìm kiếm tài liệu đầy đủ, chất lượng và có lời giải chi tiết không phải lúc nào cũng dễ dàng.
Với mong muốn giúp đỡ các em học sinh lớp 8, chúng tôi xin giới thiệu Trang tài liệu chứa 20 Đề Thi HSG Toán 8 Có Lời Giải. Tại đây, các em sẽ tìm thấy những bộ đề thi đa dạng và được chọn lọc kỹ càng từ các kỳ thi HSG Toán 8 trước đây. Đặc biệt, mỗi đề thi đi kèm với lời giải chi tiết, giúp các em hiểu rõ từng bước giải quyết vấn đề và áp dụng lý thuyết vào thực tế.
Trang tài liệu này đã được tổ chức một cách khoa học, nhằm giúp các em dễ dàng tìm kiếm và ôn tập từng chủ đề và mức độ khó. Các đề thi được biên soạn bởi những chuyên gia có kinh nghiệm, đảm bảo tính thực tế và phù hợp với nội dung kiểm tra. Lời giải chi tiết không chỉ giúp các em kiểm tra và đánh giá năng lực của mình, mà còn cung cấp những gợi ý và phương pháp giải quyết bài tập, giúp các em nắm vững kiến thức và kỹ năng trong môn Toán.
Hãy truy cập Trang tài liệu 20 Đề Thi HSG Toán 8 Có Lời Giải để tìm hiểu thêm về những bài tập thú vị và cải thiện khả năng giải quyết vấn đề của mình. Chúng tôi tin rằng, với sự cống hiến và ôn tập đều đặn, các em học sinh sẽ tiến xa trên con đường học tập và đạt được thành công trong môn Toán. Hãy bắt đầu hành trình của bạn ngay bây giờ và khám phá vẻ đẹp của toán học thông qua những đề thi HSG Toán 8!
Đề thi tham khảo
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
ĐỀ 1 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1
a) Tìm x,
y, z thỏa mãn phương trình sau
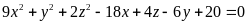 .
.
b) Giải
phương trình

Câu 2
a) Giải
phương trình
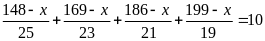
b) Chứng
minh rằng
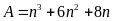 chia hết cho 48 với n chẵn.
chia hết cho 48 với n chẵn.
Câu 3
a) Tìm các giá trị của x để biểu thức:
 có giá
trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
có giá
trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
b) Chứng minh rằng nếu tổng của hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 3.
Câu 4
Cho hình vuông ABCD, M là
một điểm tuỳ ý trên đường chéo BD. Kẻ
 ,
,
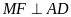 .
.
a) Chứng minh
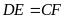
b) Chứng minh ba đường thẳng DE, BF, CM đồng quy.
c) Xác định vị trí của điểm M để diện tích tứ giác AEMF lớn nhất.
Câu 5
a) Chứng
minh rằng
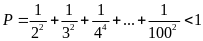
b) Cho a,
b, c là ba số khác 0 thoả mãn
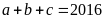 và
và
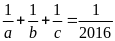
Chứng minh rằng trong ba số a, b, c tồn tại hai số đối nhau.
ĐÁP ÁN
Câu 1 (2 điểm).
a) Tìm x,
y, z thỏa mãn phương trình sau:
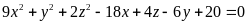 .
.
Ta có:
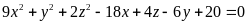

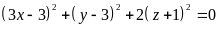
Vì
 với mọi x, y, z nên:
với mọi x, y, z nên:

b) Giải
phương trình:

Hướng dẫn

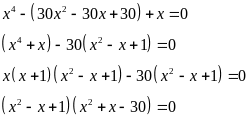
Ta có:
 với mọi
x nên suy ra:
với mọi
x nên suy ra:
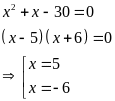
Câu 2.
Giải phương trình:
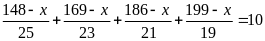
Hướng dẫn
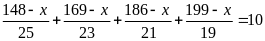
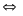
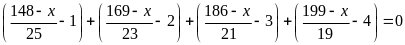
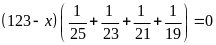
Vì
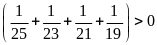 nên 123 – x = 0, suy ra x = 123.
nên 123 – x = 0, suy ra x = 123.
Chứng minh rằng:
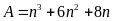 chia hết cho 48 với n chẵn.
chia hết cho 48 với n chẵn.
Hướng dẫn
 chia hết
cho 48 với n chẵn
chia hết
cho 48 với n chẵn
Ta có:

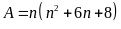

Vì n là
số chẵn nên đặt
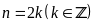 ,
khi đó:
,
khi đó:
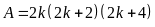
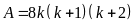

Vì
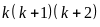 là tích của 3 số tự nhiên liên tiếp nên:
là tích của 3 số tự nhiên liên tiếp nên:
- Tồn
tại một số là bội của 2 nên
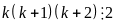 nên
nên
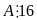
- Tồn
tại một số là bội của 3 nên
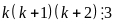
Vậy A
chia hết cho 3, 16 mà
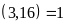 nên
nên
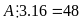 .
.
Câu 3 (2 điểm).
a) Tìm các giá trị của x để biểu thức:
 có giá
trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
có giá
trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
b) Chứng minh rằng nếu tổng của hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 3.
Hướng dẫn


Vì
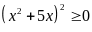 nên
nên
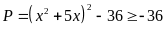 Do đó Min P
=
-36 khi
Do đó Min P
=
-36 khi
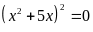 .
.
Từ đó ta tìm được x = 0 hoặc x = -5 thì min P = -36.
b) Gọi hai số phải tìm là a và b, ta có a + b chia hết cho 3.
Ta có:
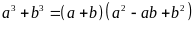
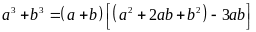
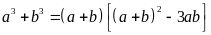
Vì
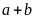 chia hết cho 3 nên
chia hết cho 3 nên
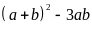 chia hết cho 3;
chia hết cho 3;
Do vậy
 chia hết cho 9.
chia hết cho 9.
Câu 4 (3 điểm).
Cho hình vuông ABCD, M là
một điểm tuỳ ý trên đường chéo BD. Kẻ ME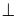 AB,
MF
AB,
MF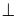 AD.
AD.
a )
Chứng minh:
)
Chứng minh:
b) Chứng minh ba đường thẳng: DE, BF, CM đồng quy.
c) Xác định vị trí của điểm M để diện tích tứ giác AEMF lớn nhất.
Hướng dẫn
a) Chứng
minh:

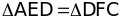
 đpcm.
đpcm.
b) DE, BF,
CM là ba đường cao của
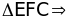 đpcm.
đpcm.
c) Có Chu vi hình chữ nhật AEMF = 2a không đổi
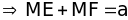 không đổi
không đổi
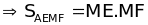 lớn nhất
lớn nhất

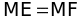 (AEMF là hình vuông)
(AEMF là hình vuông)
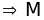 là trung
điểm của BD.
là trung
điểm của BD.
Câu 5.
Chứng minh rằng:
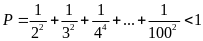
Hướng dẫn
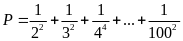
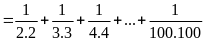



ĐỀ 2 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1
a) Phân
tích đa thức sau thành nhân tử
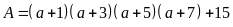
b) Cho
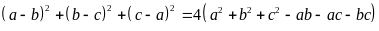
Chứng
minh rằng
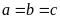 .
.
Câu 2. Tìm
giá trị nhỏ nhất của biểu thức
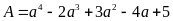 .
.
Câu 3. Tìm
số
dư trong phép
chia của
biểu
thức
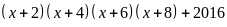 cho đa
thức
cho đa
thức
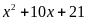 .
.
Câu 4. Cho
tam giác ABC vuông cân tại A, các điểm D, E theo thứ tự
di chuyển trên AB, AC sao cho
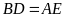 .
Xác định vị trí của điểm D, E sao cho:
.
Xác định vị trí của điểm D, E sao cho:
a) DE có độ dài nhỏ nhất.
b) Tứ giác BDEC có diện tích nhỏ nhất.
Câu 5
a) Tìm tất cả các tam giác vuông có số đo các cạnh là các số nguyên dương và số đo diện tích bằng số đo chu vi.
b) Chứng
minh rằng nếu a, b, c là số đo ba cạnh của một tam giác
vuông, với a là độ dài cạnh huyền thì thì các số
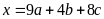 ;
;
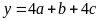 ;
;
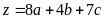 cũng là số đo ba cạnh của một tam giác vuông khác.
cũng là số đo ba cạnh của một tam giác vuông khác.
Câu 6
a) Tìm các
số x, y nguyên dương biết
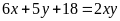
b) Tìm các
số nguyên x, y biết
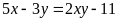
ĐÁP ÁN
Câu 1
a)
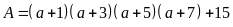
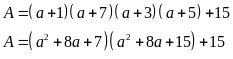
Đặt
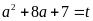 ,
ta có:
,
ta có:

Do đó
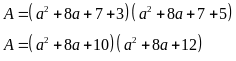
 .
.
b) Ta có:
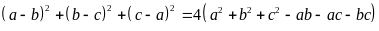
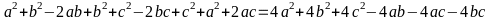
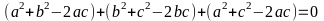
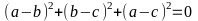
Vì
 ;
;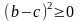 ;
;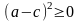 ;
với mọi a, b, c
;
với mọi a, b, c
nên (*)
xảy ra khi và chỉ khi
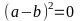 ;
; và
và

Vậy
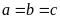 .
.
Câu 2
Ta có:
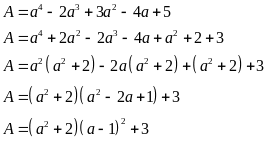
Vì
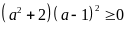 với mọi a nên
với mọi a nên
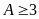
Vậy giá
trị nhỏ nhất của
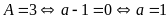 .
.
Câu 3 (2 điểm).
Tìm
số
dư trong phép
chia của
biểu
thức
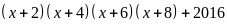 cho đa
thức
cho đa
thức
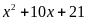 .
.
Hướng dẫn
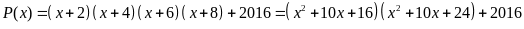
Đặt
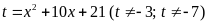 ,
biểu thức P(x) được viết lại:
,
biểu thức P(x) được viết lại:
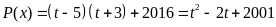
Do đó
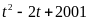 cho ta số dư là
cho ta số dư là
 .
.
Câu 4 (3 điểm).
Cho tam giác ABC vuông cân tại A, các điểm D, E theo thứ tự di chuyển trên AB, AC sao cho BD = AE. Xác định vị trí của điểm D, E sao cho:
a) DE có độ dài nhỏ nhất.
b) Tứ giác BDEC có diện tích nhỏ nhất.
Hướng dẫn

a) Đặt
AB = AC = a, DB = AE = x ( )
)
Ta có:
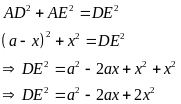
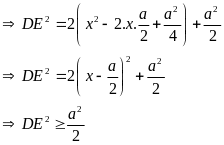
Vậy DE
nhỏ nhất bằng

Khi đó D, E lần lượt là trung điểm của AB, AC.
b) Diện
tích của tam giác ABC là:

Diện tích
tam giác ADE là:
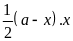
Khi đó diện tích của tứ giác BDEC là:
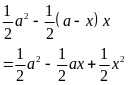

Vậy diện
tích của tứ giác BDEC nhỏ nhất bằng
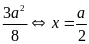
Khi đó D, E lần lượt là trung điểm của AB, AC.
Câu 5
a) Tìm tất cả các tam giác vuông có số đo các cạnh là các số nguyên dương và số đo diện tích bằng số đo chu vi.
Hướng dẫn
a) Gọi các cạnh của tam giác vuông là x, y, z trong đó cạnh huyền là z.
Theo đề bài ta có:
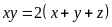 (1) và
(1) và
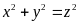
Từ
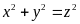
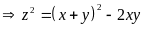 thay vào (1) ta có:
thay vào (1) ta có:
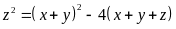
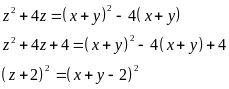
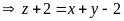
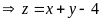 thay vào
(1) ta được:
thay vào
(1) ta được:

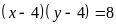
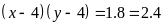
Từ đó tìm được các giá trị của x, y, z là:
(x = 5, y = 12, z = 13); (x = 12, y = 5, z=13)
(x = 6, y = 8, z = 10); (x = 8, y = 6, z = 10)
b) Theo đề
bài ta có
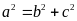
Ta có:
 mà
mà
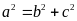
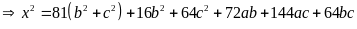
 (1)
(1)
 mà
mà
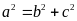
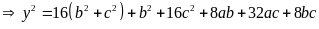
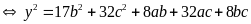 (2)
(2)
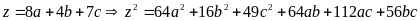 mà
mà
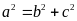
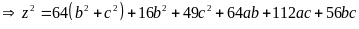
 (3)
(3)
Từ (2) và
(3) ta có
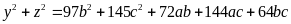 (4)
(4)
Từ (1) và
(4) suy ra
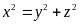
Vậy x, y, z cũng là độ dài ba cạnh của một tam giác vuông
ĐỀ 3 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1. Phân tích đa thức sau thành nhân tử
a)
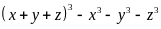
b)
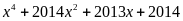
Câu 2
a) Tìm x,
biết:
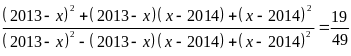
b) Chứng
minh rằng với mọi số nguyên n ta có
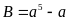 chia hết cho 30.
chia hết cho 30.
Câu 3
Cho tam giác ABC vuông tại A, D là điểm di động trên cạnh BC. Gọi E, F lần lượt là hình chiếu vuông góc của điểm D lên AB, AC.
a) Xác định vị trí của điểm D để tứ giác AEDF là hình vuông.
b) Xác định vị trí của điểm D sao cho 3AD + 4EF đạt giá trị nhỏ nhất.
Câu 4
Tìm tất cả các số chính phương gồm 4 chữ số biết rằng khi ta thêm 1 đơn vị vào chữ số hàng nghìn, thêm 3 đơn vị vào chữ số hàng trăm, thêm 5 đơn vị vào chữ số hàng chục, thêm 3 đơn vị vào chữ số hàng đơn vị ta vẫn được một số chính phương.
Câu 5
Cho a, b dương
và
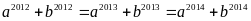 .
Tính
.
Tính
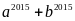
ĐÁP ÁN
Câu 1 (2 điểm). Phân tích đa thức sau thành nhân tử:
a)
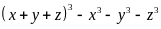
b)
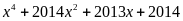
Hướng dẫn
a)
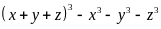
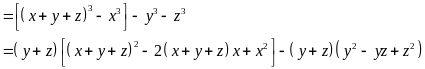
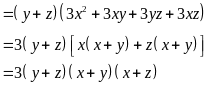
b)
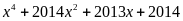

Câu 2 (2 điểm).
a) Tìm x,
biết:
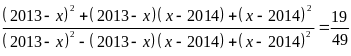 .
.
b) Chứng
minh rằng với mọi số nguyên n ta có:
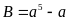 chia hết cho 30.
chia hết cho 30.
Hướng dẫn
a) ĐKXĐ:
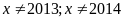
Đặt

Ta có:
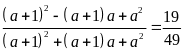

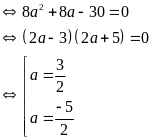
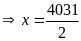 hoặc
hoặc
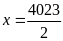 .
.
b) Ta có:
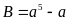

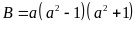
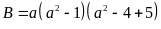
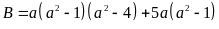

Vì
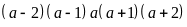 là tích của 5 số tự nhiên liên tiếp nên tồn tại
một số là bội của 5, do đó
là tích của 5 số tự nhiên liên tiếp nên tồn tại
một số là bội của 5, do đó
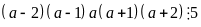 (1)
(1)
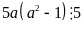 (2)
(2)
Từ (1)
và (2) suy ra
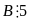
Câu 3 (2 điểm).
Cho tam giác ABC vuông tại A, D là điểm di động trên cạnh BC. Gọi E, F lần lượt là hình chiếu vuông góc của điểm D lên AB, AC.
a) Xác định vị trí của điểm D để tứ giác AEDF là hình vuông.
b) Xác định vị trí của điểm D sao cho 3AD + 4EF đạt giá trị nhỏ nhất.
Hướng dẫn

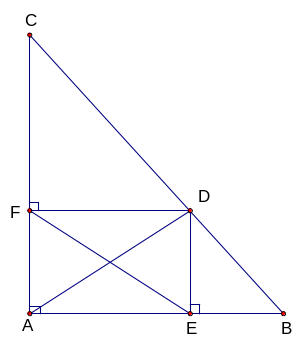
a) Tứ giác AEDF là hình
chữ nhật (vì
 )
)
Để tứ giác AEDF là hình
vuông thì AD là tia phân giác của
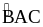 .
.
b) Do tứ giác AEDF là hình chữ nhật nên AD = EF
Suy ra 3AD + 4EF = 7AD
3AD + 4EF nhỏ nhất
 AD
nhỏ nhất,
AD nhỏ nhất khi D là hình chiếu của A trên BC.
AD
nhỏ nhất,
AD nhỏ nhất khi D là hình chiếu của A trên BC.
Câu 4 (2 điểm).
Tìm tất cả các số chính phương gồm 4 chữ số biết rằng khi ta thêm 1 đơn vị vào chữ số hàng nghìn , thêm 3 đơn vị vào chữ số hàng trăm, thêm 5 đơn vị vào chữ số hàng chục, thêm 3 đơn vị vào chữ số hàng đơn vị , ta vẫn được một số chính phương.
Hướng dẫn
Gọi số
phải tìm là
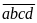 với
với
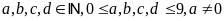
Theo đề bài ta có:
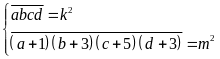
Suy ra:
 với
với
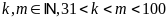
Do đó
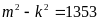
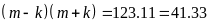
Vì
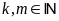 nên
nên
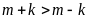 .
.
Do đó:
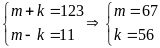 hoặc
hoặc
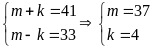
Kết luận
đúng
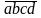 = 3136
= 3136
Câu 5 (2 điểm)
Cho a, b dương
và
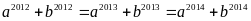 .
.
Tính
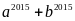 .
.
Hướng dẫn
Ta có:
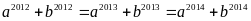

 (vì
(vì
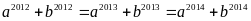 )
)
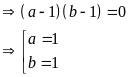
Với a = 1
thì
 hoặc
hoặc
 (loại)
(loại)
Với b = 1
thì
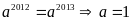 hoặc
hoặc
 (loại)
(loại)
Vậy a = 1, b = 1
Do đó
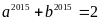 .
.
ĐỀ 4 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1
a) Tìm
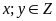 thoả
mãn
thoả
mãn
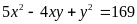 .
.
b) Chứng
minh rằng với mọi số nguyên n thì biểu thức:
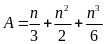 có giá trị là một số nguyên.
có giá trị là một số nguyên.
Câu 2
a) Cho hai
số
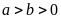 .
So sánh hai số
.
So sánh hai số
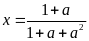 và
và
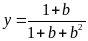 .
.
b) Tìm
x, biết
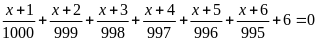 .
.
Câu 3
Gọi M, N theo thứ tự là trung điểm các cạnh AB, BC của hình vuông ABCD. Các đường thẳng DN và CM cắt nhau tại I. Chứng minh tam giác AID là tam giác cân.
Câu 4
Tìm cặp
số nguyên
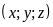 thỏa mãn phương trình:
thỏa mãn phương trình:
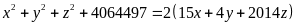
Câu 5.
Chứng minh
rằng nếu n là số tự nhiên sao cho
 và
và
 đều là các số chính phương thì n là bội số của 24.
đều là các số chính phương thì n là bội số của 24.
ĐÁP ÁN
Câu 1 (2 điểm).
a) Tìm
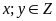 thoả
mãn:
thoả
mãn:
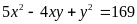 .
.
b) Chứng
minh rằng với
mọi số nguyên n thì biểu thức:
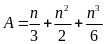 có giá trị là một số nguyên.
có giá trị là một số nguyên.
Hướng dẫn
a) Ta có:
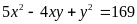
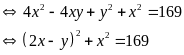

Từ (I) ta có:
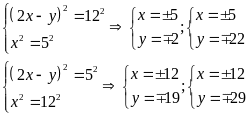
Từ (II) ta có:
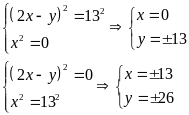
Vậy
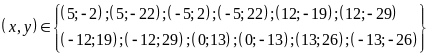
b) Ta có:
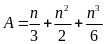

Vì
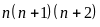 là tích của ba số tự nhiên liên tiếp nên
là tích của ba số tự nhiên liên tiếp nên
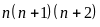
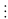 3
và
3
và
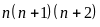
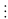 2
mà
2
mà
 .
Do
đó
.
Do
đó
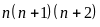
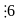 .
.
Hay A là một số nguyên.
Câu 2 (2 điểm).
a) Cho hai
số
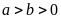 .
So sánh hai số
.
So sánh hai số
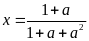 và
và
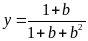 .
.
b) Tìm
x, biết:
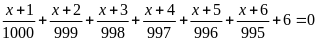
Hướng dẫn
Vì
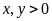 ,
ta có:
,
ta có:
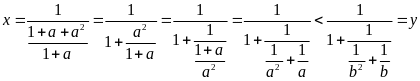
Vì
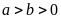 nên
nên
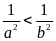 và
và
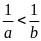 .
.
Vậy
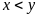 .
.
b) Ta có:
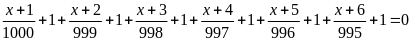
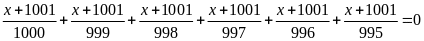
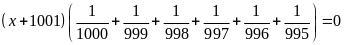
Vì
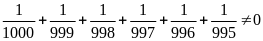 nên
nên
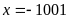 .
.
Câu 3.
Câu 3
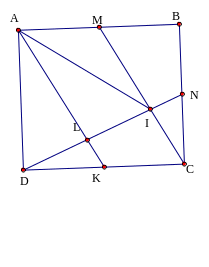
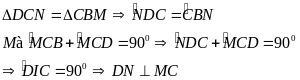
goi K là
trung điểm của DC nên AM=KC,
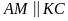
Nên AMCK là hình bình hành
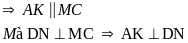
Hay
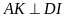 (1)
(1)
Goi L là
giao điiểm của DN và AK. K là trung điểm của DC và
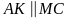
suy ra AK đi qua trung điểm của DI nên L là trung điểm của DI (2)
Từ (1) và (2) suy ra tam giác AID cân tại A
Câu 4.
Đặt
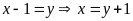 .
Ta có:
.
Ta có:
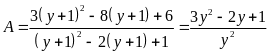
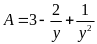
Đặt
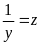
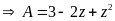
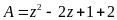
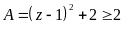
Vậy min
 .
.
ĐỀ 5 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1
a) Phân tích đa thức sau
thành nhân tử
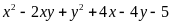
b) Chứng minh
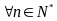 thì
thì
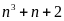 là hợp số.
là hợp số.
c) Cho hai số chính phương liên tiếp. Chứng minh rằng tổng của hai số đó cộng với tích của chúng là một số chính phương lẻ.
Câu 2
a) Giải
phương trình
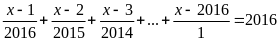
b) Cho
 .
Tính
.
Tính

Câu 3
a)
Tìm giá trị nhỏ nhất của biểu thức
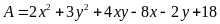
b) Cho a; b; c là ba cạnh của tam giác.
Chứng
minh
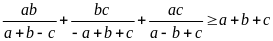
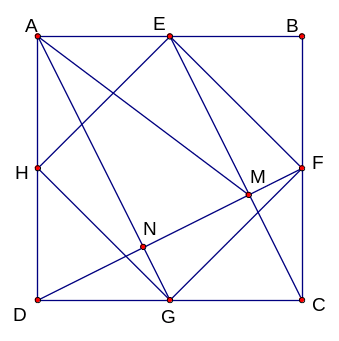
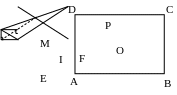
Câu 4. Cho hình vuông ABCD có cạnh bằng a. Gọi E; F; G; H lần lượt là trung điểm của các cạnh AB, BC; CD; DA. M là giao điểm của CE và DF.
a) Chứng minh: Tứ giác EFGH là hình vuông.
b) Chứng
minh
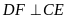 và
và
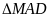 cân.
cân.
c) Tính
diện tích
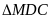 theo a.
theo a.
Bài tập tương tự câu 1b)
1. Tìm số tự nhiên n để
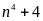 là số nguyên tố.
là số nguyên tố.
2. Cho biểu thức
 .
Tìm số tự nhiên n để biểu thức trên là số nguyên tố
.
Tìm số tự nhiên n để biểu thức trên là số nguyên tố
ĐÁP ÁN
Câu |
Ý |
Nội dung |
Điểm |
Câu 1 3 điểm |
a. 1 điểm |
= (x - y)2 +4(x - y) - 5 = (x - y)2 + 4(x - y)2 + 4 -9 = (x - y + 2)2 - 32 = ( x - y + 5)(x - y -1) |
0.5 0,5 |
b. 1 điểm |
Ta có: n3 + n + 2 = n3 + 1+ n+1= (n + 1)( n2 - n + 1) + (n + 1) =(n+1)( n2 - n + 2) Do
|
0.25 0,25 0.5 |
|
c. 1 điểm |
Gọi hai số lần lượt là a2 và (a+1)2 Theo bài ra ta có: a2 + (a + 1)2 + a2( a + 1)2 = a4 +2a3 + 3a2 + 2a + 1 = (a4 + 2a3 + a2) + 2(a2 + a) + 1 = (a2 + a)2 + 2(a + 1) + 1 =
( a2
+ a + 1)2
là một số chính phương lẻ vì a2
+
a = a(a + 1) là số chẵn
|
0.25 0.25 0.25
0.25 |
|
Câu 2 2 điểm |
a. 1.5 điểm |
Phương trình đã cho tương đương với:
|
0.5 0. 5
0. 5 |
b. 0.5 điểm |
a2
+
b2
+
c2
= a3
+ b3
+ c3
= 1
|
0.25
0.25
|
|
Câu 3 1.5 điểm |
a. 1 điểm |
Ta có: A = 2(x2 + 2xy + y2) + y2 -8x -2y + 18 A = 2[(x+y)2 - 4(x + y) +4] + ( y2 + 6y +9) + 1 A
= 2(x + y - 2)2
+ (y+3)2
+ 1
Vậy minA = 1 khi x = 5; y = -3 |
0.25 0.25 0.25 0.25 |
b. 0.5 điểm |
vì a; b; c là ba cạnh của tam giác nên: a + b - c > 0; - a + b + c > 0; a - b + c > 0. Đặt x = - a + b + c >0; y = a - b + c >0; z = a + b - c >0 ta
có: x + y + z = a + b + c;
Mà x + y + z = a + b + c nên suy ra điều phải chứng minh |
0.25
0.25 |
|
Câu 4 3.5 điểm |
Hình vẽ 0. 5 đ |
|
0.5 |
|
a. 1.25 điểm |
Chứng minh: EFGH là hình thoi Chứng minh có 1 góc vuông. Kết luận Tứ giác EFGH là Hình vuông |
0. 5 0. 5 0.25 |
b. 1 điểm |
Hay
CE
Gọi
N là giao điểm của AG và DF. Chứng minh tương tự: AG
|
0.25 0.25
0.25
0.25 |
|
|
c. 0.75 điểm |
Do
đó :
Mà
:
Vậy
:
Trong
Do
đó :
|
0.25
0.25
0.25 |
Bài tập tương tự câu 1b)
1. Tìm số tự nhiên n để
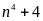 là số nguyên tố.
là số nguyên tố.
2. Cho biểu thức
 .
Tìm số tự nhiên n để biểu thức trên là số nguyên tố
.
Tìm số tự nhiên n để biểu thức trên là số nguyên tố
1. Ta có
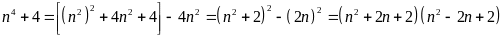
Vì
 với mọi số tự nhiên n, do đó để
với mọi số tự nhiên n, do đó để
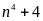 là số nguyên tố thì
là số nguyên tố thì

2. Ta có

Lập luận tương tự như trên
ĐỀ 6 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1.
Giải
phương trình:
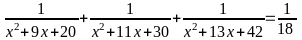
Câu 2. Cho
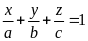 và
và
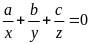 .
Chứng minh rằng :
.
Chứng minh rằng :
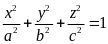 .
.
Câu 3. Cho
a, b, c khác nhau đôi một và
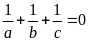 .
Rút gọn biểu thức:
.
Rút gọn biểu thức:
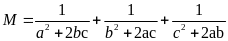
Câu 4. Cho
a, b, c là 3 số khác 0 thoả mãn
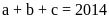 và
và
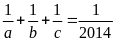 .
.
Chứng minh rằng trong 3 số a, b, c tồn tại hai số đối nhau.
Câu 5. Tìm
GTNN của
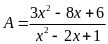
Bài tập tương tự
Bài 1. Cho
a, b, c khác nhau đôi một và
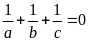 .
Rút gọn các biểu thức:
.
Rút gọn các biểu thức:
a,
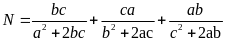
b,
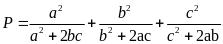
Bài 2. Tìm
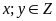 thoả
mãn:
thoả
mãn:
a)
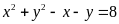
b)

Bài 3.
a) Tìm
GTNN của
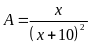 b) Tìm
GTNN của
b) Tìm
GTNN của
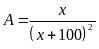
c) Tìm
GTNN của
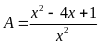 d) Tìm
GTNN của
d) Tìm
GTNN của

Bài 4.
a) Tìm
GTNN của
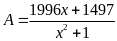
b) Tìm
GTNN của
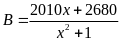
HƯỚNG DẪN
Câu 1.
Giải
phương trình:
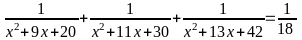
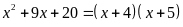
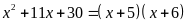
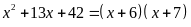
ĐKXĐ:
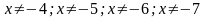
Giải phương trình:



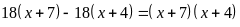
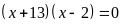
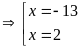
Câu 2. Cho
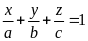 và
và
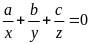 .
Chứng
minh rằng :
.
Chứng
minh rằng :
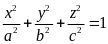 .
.
Hướng dẫn
Từ

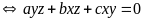
Ta có:
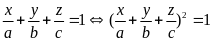
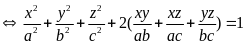
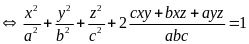

Câu 3. Cho
a, b, c khác nhau đôi một và
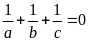 .
Rút gọn biểu thức:
.
Rút gọn biểu thức:
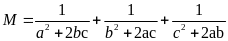
Hướng dẫn
Theo đề bài ta có:
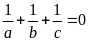
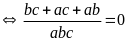


Ta có:
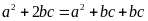
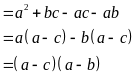
Tương tự ta có:
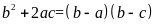
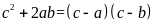
Vậy
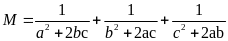
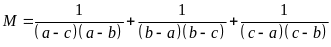
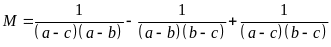
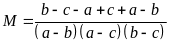
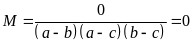
Câu 4. Cho
a, b, c là 3 số khác 0 thoả mãn
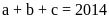 và
và
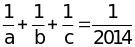 .
.
Chứng minh rằng trong 3 số a, b, c tồn tại hai số đối nhau.
Hướng dẫn
Theo đề bài ta có:
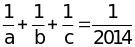
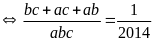
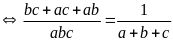 (vì
(vì
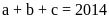 )
)

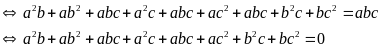
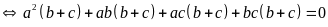
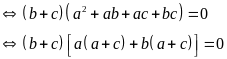
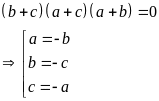
Vậy trong 3 số a, b, c tồn tại hai số đối nhau.
Câu 5. Tìm
GTNN của
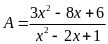
Hướng dẫn
Đặt
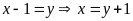 .
Ta có:
.
Ta có:
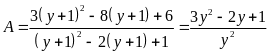
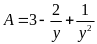
Đặt
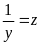
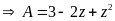
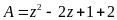
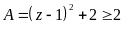
Vậy min
 .
.
Bài 1. Tìm
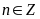 để
để
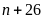 và
và
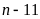 đều là lập phương của một số tự nhiên.
đều là lập phương của một số tự nhiên.
Giải
Đặt
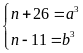
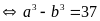
Ta có:
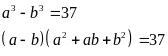
Suy ra
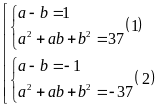
Từ (1) ta
có:
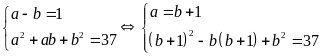

Do đó
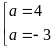
Với
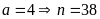
Với

Từ (2) ta
có
 (Loại)
(Loại)
Bài 2. Cho
biểu thức
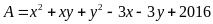 .
Tìm giá trị của x, y để A đạt giá trị nhỏ nhất.
.
Tìm giá trị của x, y để A đạt giá trị nhỏ nhất.
Giải
Cách 1
Ta có:
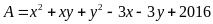
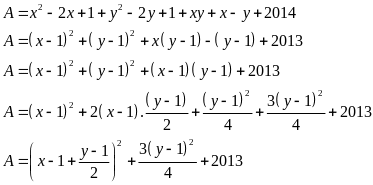
Do đó
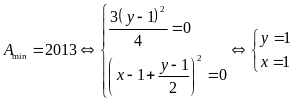
Cách 2
Ta có:
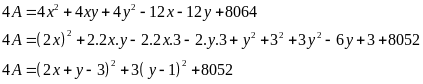
Do đó

Vậy
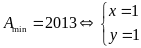
Bài 3. Tìm
nghiệm tự nhiên (x; y) của
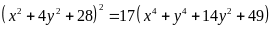
Giải
Ta có:
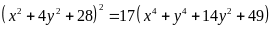


Bài 4. Tìm giá trị nhỏ nhất của các biểu thức:
a)
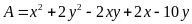 với
với
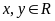 .
.
b)
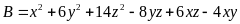 .
.
c)
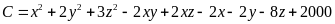 .
.
Bài 1. a)
Tìm n để
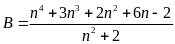 có
giá trị là một số nguyên.
có
giá trị là một số nguyên.
b) Tìm n để
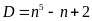 là số chính phương
là số chính phương
 .
.
Hướng dẫn
a)
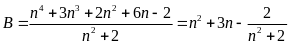
B có giá
trị nguyên khi
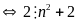
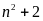 là ước
tự nhiên của 2.
là ước
tự nhiên của 2.
 không có
giá trị nào thỏa mãn.
không có
giá trị nào thỏa mãn.

 thì B nhận
giá trị nguyên.
thì B nhận
giá trị nguyên.
b)
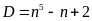
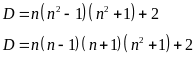

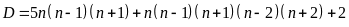
Vì
 và
và

Vậy D chia 5 dư 2
Do đó số D có tận cùng là 2 hoặc 7 nên D không phải số chính phương.
Bài 2. Giải phương trình:
a)
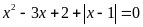 .
.
b)
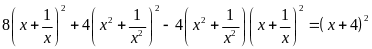 .
.
Hướng dẫn
a)
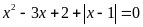 (1)
(1)
+ Nếu
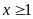 :
(1)
:
(1)
 (thỏa mãn điều kiện
(thỏa mãn điều kiện
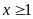 )
)
+ Nếu
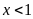 :
(1)
:
(1)

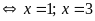 (cả hai đều không thảo
mãn)
(cả hai đều không thảo
mãn)
Vậy phương trình có
nghiệm duy nhất
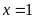 .
.
b)
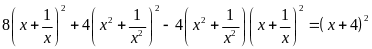 (2)
(2)
ĐKXĐ:
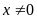
(2)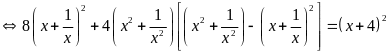
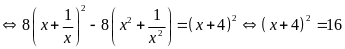
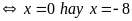 và
và
 .
.
Vậy phương trình đã cho
có một nghiệm
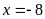
Bài 3. Cho
ba số thực a, b, c thỏa mãn điều kiện
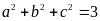 và
và
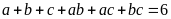 .
Tính giá trị của biểu thức:
.
Tính giá trị của biểu thức:
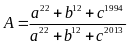 .
.
Hướng dẫn:
Ta có:
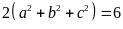
Suy ra:
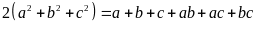
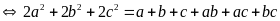

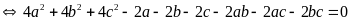
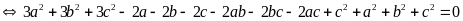
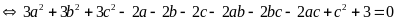 (vì
(vì
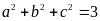 )
)

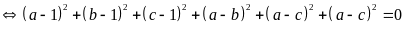
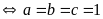
Vậy
 .
.
Bài 4. Cho hình bình hành ABCD. Qua A kẻ đường thẳng tùy ý cắt BD, BC, CD lần lượt ở E, K, G. Chứng minh:
a)
 .
.
b)
 .
.
c) Khi đường thẳng d thay đổi thì tích BK.DG có giá trị không đổi.
Hướng dẫn:
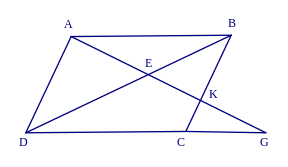
a) Ta có
AD // BK nên
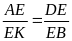 (1)
(1)
AB // CD
nên
 (2)
(2)
Từ (1) và
(2) suy ra
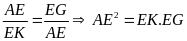 .
.
b) Ta có

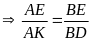 (3)
(3)
Tương tự
ta có:
 (4)
(4)
Cộng vế với vế của (3) và (4) ta có:


 .
.
c) Ta có:
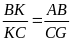 và
và
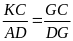 nhân từng vế của đẳng thức trên ta được
nhân từng vế của đẳng thức trên ta được
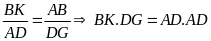 không đổi
không đổi
ĐỀ 7 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1 (2 điểm)
a) Rút gọn
biểu thức
 .
.
b) Cho
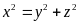 .
Chứng minh rằng
.
Chứng minh rằng
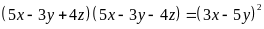
Câu 2 (2 điểm)
a) Phân
tích đa thức sau thành nhân tử
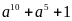 .
.
b) Cho
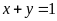 và
và
 .
Chứng minh rằng
.
Chứng minh rằng
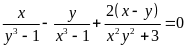 .
.
Câu 3 (2 điểm)
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo. Qua O kẻ đường thẳng song song với hai đáy cắt BC ở I, cắt AD ở J. Chứng minh:
a)
 .
.
b)
 .
.
Câu 4 (1 điểm)
Cho hình
thang ABCD (AD // BC) có hai đường chéo cắt nhau tại O.
Tính diện tích tam giác AOB, biết diện tích tam giác BOC
là 169
 và diện tích tam giác AOD là 196
và diện tích tam giác AOD là 196
 .
.
Câu 5 (1 điểm)
Tìm nghiệm
nguyên dương của phương trình sau
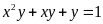
ĐÁP ÁN
Câu 1 (2 điểm)
a) Rút gọn
biểu thức
 .
.
b) Cho
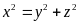 .
Chứng minh rằng
.
Chứng minh rằng
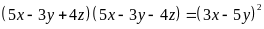
Hướng dẫn
a) Ta có:
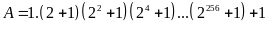
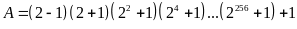
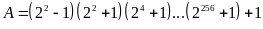

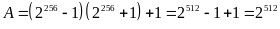 .
.
b) Ta có:
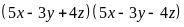
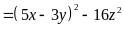

 (vì
(vì
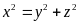 )
)
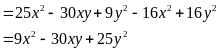
 .
.
Câu 2 (2 điểm)
a) Phân
tích đa thức sau thành nhân tử
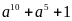 .
.
b) Cho
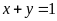 và
và
 .
Chứng minh rằng
.
Chứng minh rằng
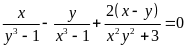 .
.
Hướng dẫn
a)
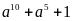
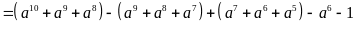
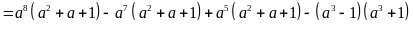
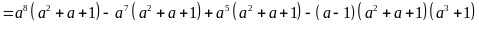
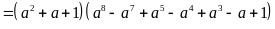 .
.
b) Ta có:
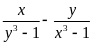
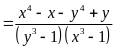

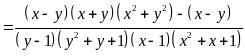
Vì
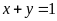
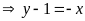 và
và
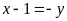 ,
do đó ta có:
,
do đó ta có:
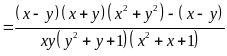
 (vì
(vì
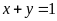 )
)
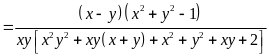


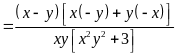
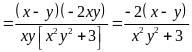
Do đó
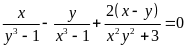 .
.
Câu 3 (2 điểm)
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo. Qua O kẻ đường thẳng song song với hai đáy cắt BC ở I, cắt AD ở J. Chứng minh:
a)
 .
.
b)
 .
.
Hướng dẫn

a) Ta có:
OI // AB,
xét tam giác OIC ta có:
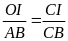 (1).
(1).
OI // CD,
xét tam giác BDC ta có:
 (2).
(2).
Cộng vế với vế của (1) và (2) ta có:
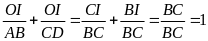
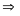
 (3).
(3).
b) Chứng
minh tương tự ta có
 (4).
(4).
Cộng vế
với vế của (3) và (4) ta có:
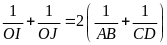
Lại có
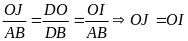 ,
do đó ta có:
,
do đó ta có:
 .
.
Câu 4 (1 điểm)
Cho hình
thang ABCD (AD // BC) có hai đường chéo cắt nhau tại O.
Tính diện tích tam giác AOB, biết diện tích tam giác BOC
là 169
 và diện tích tam giác AOD là 196
và diện tích tam giác AOD là 196
 .
.
Hướng dẫn

Ta chứng
minh được
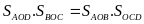 mà
mà
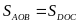
Do đó
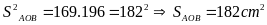
Câu 5 (1 điểm)
Tìm nghiệm
nguyên dương của phương trình sau
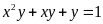
Hướng dẫn
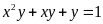
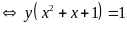 vì
vì
 với mọi x nên phương trình có nghiệm nguyên dương khi:
với mọi x nên phương trình có nghiệm nguyên dương khi:
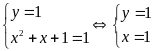
ĐỀ 8 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1 (2 điểm)
Cho

a) Tìm ĐKXĐ rồi rút gọn M.
b) Tìm a
sao cho
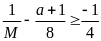 .
.
Câu 2 (2 điểm)
a) Giải
phương trình
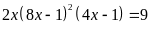 .
.
b)
Với mọi
 thì
thì
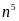 và n luôn có chữ số tận cùng giống nhau.
và n luôn có chữ số tận cùng giống nhau.
Câu 3 (3 điểm)
Cho hình thang ABCD (AB // CD), O là giao điểm hai đường chéo. Qua O kẻ đường thẳng song song với AB cắt DA tại E, cắt BC tại F.
a) Chứng minh
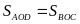 .
.
b)
Chứng minh:
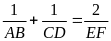
c) Gọi K là điểm bất kì thuộc OE. Nêu cách dựng đường thẳng đi qua K và chia đôi diện tích tam giác DEF.
Câu 4 (2 điểm)
Cho

Chứng
minh rằng
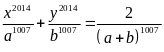 .
.
Câu 5 (1 điểm)
Tìm giá
trị nhỏ nhất của biểu thức
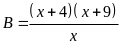 với
với
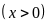 .
.
ĐÁP ÁN
Câu 1 (2 điểm)
Cho

a) Tìm ĐKXĐ rồi rút gọn M.
b) Tìm a
sao cho
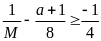 .
.
Hướng dẫn
a) ĐKXĐ
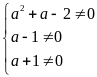

Ta có

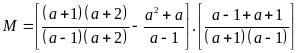
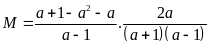
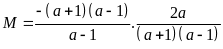

b) Ta có
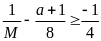
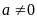
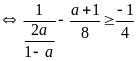
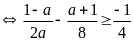

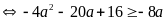


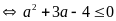
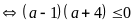
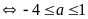 vì
vì
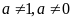 nên
nên
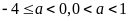
Câu 2 (2 điểm)
a) Giải
phương trình
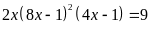 .
.
b)
Với mọi
 thì
thì
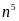 và n luôn có chữ số tận cùng giống nhau.
và n luôn có chữ số tận cùng giống nhau.
Hướng dân
a)
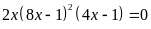
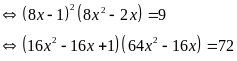
Đặt
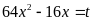 ,
ta có:
,
ta có:
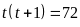 ,
do đó
,
do đó
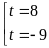
Từ đó tìm được các giá trị của x.
b) Xét hiệu:


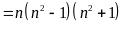
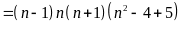
Vậy
 (1)
(1)

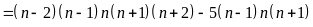
Vì
 chia hết cho 5,
chia hết cho 5,
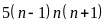 chia hết cho 5.
chia hết cho 5.
Vậy
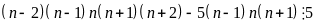 (2)
(2)
Từ (1) và
(2) suy ra
 chia hết cho 2, 5 mà
chia hết cho 2, 5 mà
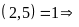
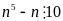
Vậy
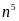 và n luôn có chữ số tận cùng giống nhau.
và n luôn có chữ số tận cùng giống nhau.
Câu 3 (3 điểm)
Cho hình thang ABCD (AB // CD), O là giao điểm hai đường chéo. Qua O kẻ đường thẳng song song với AB cắt DA tại E, cắt BC tại F.
a) Chứng minh
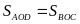 .
.
b)
Chứng minh:
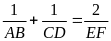
c) Gọi K là điểm bất kì thuộc OE. Nêu cách dựng đường thẳng đi qua K và chia đôi diện tích tam giác DEF.
Hướng dẫn
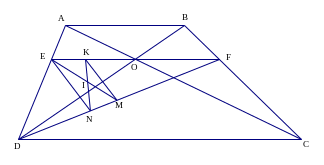
a) Ta có
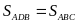 vì có cùng chiều cao hạ từ D và C xuống AB (do AB // CD)
và cạnh đáy AB.
vì có cùng chiều cao hạ từ D và C xuống AB (do AB // CD)
và cạnh đáy AB.
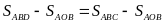 hay
hay
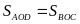 .
.
b) V×
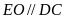
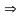
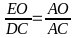 .
MÆt kh¸c
.
MÆt kh¸c
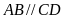
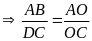 .
.

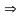
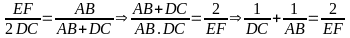 .
.
c) Dụng trung tuyến
 .
.
Dựng
 ,
nối K với N.
,
nối K với N.
KN là đường thẳng phải dựng.
Chứng minh
Ta có
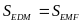 (1).
(1).
Gọi giao điểm của EM và
KN là I thì
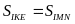 (chứng minh phần a).
(chứng minh phần a).
Từ (1) và (2) suy ra

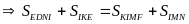
Vậy
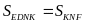 .
.
Câu 4 (2 điểm)
Cho

Chứng
minh rằng
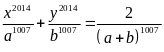 .
.
Hướng dẫn
Ta có:
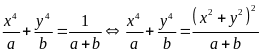 (vì
(vì
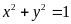 )
)
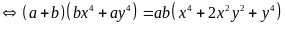

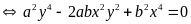
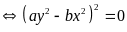

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
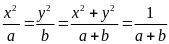
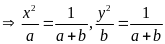
Vậy
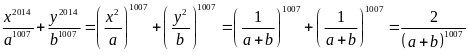 .
.
Câu 5 (1 điểm)
Tìm giá
trị nhỏ nhất của biểu thức
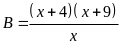 với
với
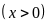 .
.
Hướng dẫn
Ta có:
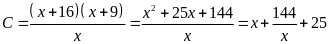
Vì
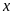 và
và
 là các số dương có tích không đổi nên có tổng nhỏ
nhất
là các số dương có tích không đổi nên có tổng nhỏ
nhất
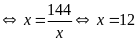
Vậy min
 .
.
ĐỀ 9 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Bài 1 (2 điểm)
Cho biểu
thức

a) Rút gọn P.
b) Với
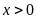 thì P không nhận những giá trị nào?
thì P không nhận những giá trị nào?
c) Tìm các giá trị của x để P nhận giá trị nguyên?
Bài 2 (2 điểm)
a) Chứng
minh rằng
 chia hết cho 72 với mọi số nguyên n.
chia hết cho 72 với mọi số nguyên n.
b) Tìm các
số nguyên dương x, y biết
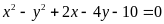 .
.
Bài 3 (3 điểm)
Cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo BD. Gọi E, F lần lượt là hình chiếu của B và D xuống đường thẳng AC. Gọi H và K lần lượt là hình chiếu của C xuống đường thẳng AB và AD.
a) Tứ giác BEDF là hình gì? Hãy chứng minh điều đó?
b) Chứng minh rằng: CH.CD = CB.CK.
c) Chứng
minh rằng:
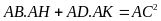 .
.
Câu 4 (2 điểm)
Cho
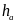 ,
,
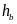 ,
,
 là độ dài các đường cao ứng với các cạnh a, b, c của
một tam giác.
là độ dài các đường cao ứng với các cạnh a, b, c của
một tam giác.
Hãy xác
định dạng của tam giác đó nếu
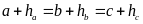 .
.
Câu 5 (1 điểm)
a) Tìm x,
y, z biết
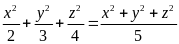 .
.
b) Cho hai
số x, y thỏa mãn
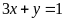 .
Tìm giá trị nhỏ nhất của biểu thức
.
Tìm giá trị nhỏ nhất của biểu thức

ĐÁP ÁN
Câu 3
Giải
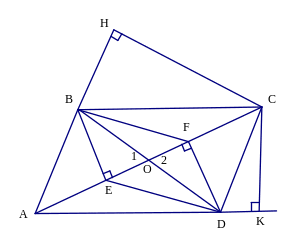
a) Ta có:
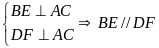 (1)
(1)
Xét
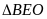 và
và
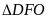 có:
có:
BO = OD (vì O là giao điểm hai đường chéo của hình bình hành ABCD)
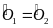 (đối
đỉnh)
(đối
đỉnh)
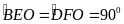
Do đó
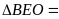
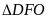 (cạnh huyền – góc nhọn)
(cạnh huyền – góc nhọn)
Suy ra BE = DF (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành.
b) Xét
 và
và
 có:
có:

Vì tứ
giác ABCD là hình bình hành nên
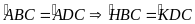 (cùng bù với hai góc bằng nhau)
(cùng bù với hai góc bằng nhau)
Do đó
 ~
~ (g.g)
(g.g)
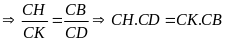 .
.
c) Ta có:
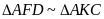
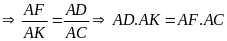
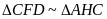
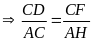 mà
mà

Do đó
 .
.
ĐỀ 10 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1
a) Phân
tích đa thức sau thành nhân tử:
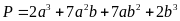 .
.
b) Giải
phương trình:
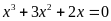 .
.
Câu 2
a) Chứng
minh rằng
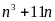 chia hết cho 6 với mọi số nguyên n.
chia hết cho 6 với mọi số nguyên n.
b) Cho
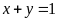 .
Tìm giá trị nhỏ nhất của
.
Tìm giá trị nhỏ nhất của
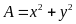 .
.
Câu 3
Cho biểu
thức
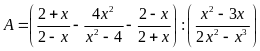
a) Tìm ĐKXĐ rồi rút gọn A.
b) Tìm giá
trị của x để
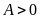 .
.
Câu 4
a) Tìm các
giá trị nguyên của x để giá trị của biểu thức
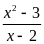 là số nguyên?
là số nguyên?
b) Cho
 .
Chứng minh rằng
.
Chứng minh rằng
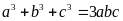 .
.
Câu 5
Cho hình chữ nhật ABCD. Trên đường chéo BD lấy điểm P khác trung điểm của BD, gọi M là điểm đối xứng của điểm C qua P.
a) Tứ giác AMDB là hình gì? Vì sao?
b) Gọi E và F lần lượt là hình chiếu của điểm M lên AB, AD. Chứng minh EF song song với AC và ba điểm E, F, P thẳng hàng.
Câu 6
Cho
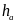 ,
,
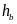 là độ dài các đường cao ứng với các cạnh a, b của
một tam giác.
là độ dài các đường cao ứng với các cạnh a, b của
một tam giác.
Hãy xác
định dạng của tam giác đó nếu
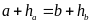 .
.
Hướng dẫn chấm
Câu 1
a) Phân
tích đa thức sau thành nhân tử:
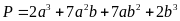 .
.
b) Giải
phương trình:
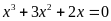 .
.
Giải
a) Ta có:
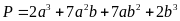
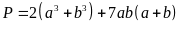
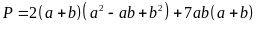


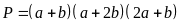
b)
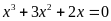
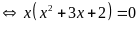

Vậy
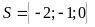
Câu 2
a) Chứng
minh rằng
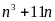 chia hết cho 6 với mọi số nguyên n.
chia hết cho 6 với mọi số nguyên n.
b) Cho
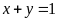 .
Tìm giá trị nhỏ nhất của
.
Tìm giá trị nhỏ nhất của
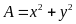 .
.
Giải
a) Ta có:
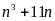

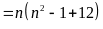
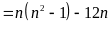
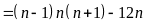
Vì
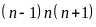 là tích của ba số tự nhiên liên tiếp nên
là tích của ba số tự nhiên liên tiếp nên
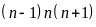 chia hết cho 6 và
chia hết cho 6 và
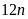 chia hết cho 6.
chia hết cho 6.
Do đó
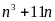 chia hết cho 6 với mọi số nguyên n.
chia hết cho 6 với mọi số nguyên n.
b) Cách 1
Từ
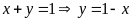 ,
do đó ta có:
,
do đó ta có:

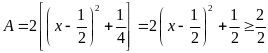
Vậy min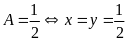 .
.
Cách 2
Ta có:
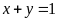
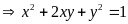 .
(1)
.
(1)
Mặt khác
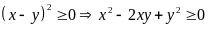 (2)
(2)
Cộng vế với vế của (1) và (2) ta có:

Vậy min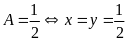 .
.
Cho biểu
thức
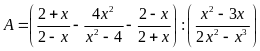
a) Tìm ĐKXĐ rồi rút gọn A.
b) Tìm giá
trị của x để
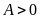 .
.
Giải
a)
ĐKXĐ:
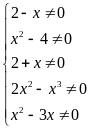

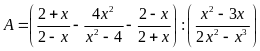

b)
ĐỀ 11 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Bài 1.
a) Phân tích đa thức sau thành nhân tử (với hệ số là các số nguyên):
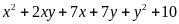 .
.
b) Biết
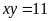 và
và
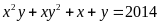 .
Hãy tính
.
Hãy tính
 .
.
Bài 2. Tìm x, biết
a)
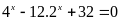 .
.
b)
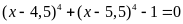
Bài 3. Cho
biểu thức:
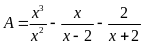
a) Rút gọn A.
b) Với
giá trị nào của x thì
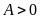 ,
,
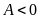 ?
?
c) Tìm x
để
 .
.
Bài 4. Cho
tam giác ABC vuông tại A
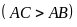 ,
đường cao AH
,
đường cao AH
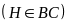 .
Trên tia HC lấy điểm D sao cho HD = HA. Đường vuông góc
với BC tại D cắt AC tại E.
.
Trên tia HC lấy điểm D sao cho HD = HA. Đường vuông góc
với BC tại D cắt AC tại E.
a) Chứng
minh
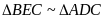 .
Tính độ dài đoạn thẳng BE theo
.
Tính độ dài đoạn thẳng BE theo
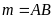 .
.
b) Gọi M
là trung điểm của đoạn BE. Chứng minh rằng
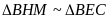 .
Tính
.
Tính
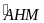 .
.
c) Tia AM
cắt BC tại G. Chứng minh
 .
.
Bài 5. Cho
a, b, c từng đôi một khác nhau thoả mãn:
 .
.
Rút gọn
biểu thức:
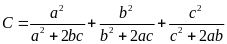 .
.
HƯỚNG DẪN
Câu 4. Cho
tam giác ABC vuông tại A
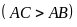 ,
đường cao AH
,
đường cao AH
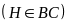 .
Trên tia HC lấy điểm D sao cho HD = HA. Đường vuông góc
với BC tại D cắt AC tại E.
.
Trên tia HC lấy điểm D sao cho HD = HA. Đường vuông góc
với BC tại D cắt AC tại E.
a) Chứng
minh
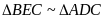 .
Tính độ dài đoạn thẳng BE theo
.
Tính độ dài đoạn thẳng BE theo
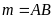 .
.
b) Gọi M
là trung điểm của đoạn BE. Chứng minh rằng
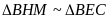 .
Tính
.
Tính
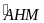 .
.
c) Tia AM
cắt BC tại G. Chứng minh
 .
.
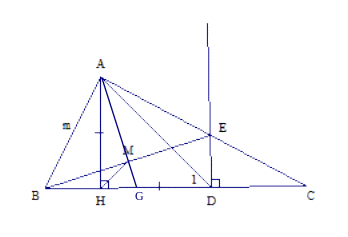
a) Xét
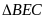 và
và
 có:
có:
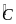 :
chung
:
chung
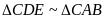 (vì
(vì
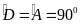 ,
,
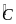 chung)
chung)
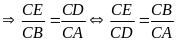
Do đó
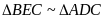 (c.g.c)
(c.g.c)
Theo đề
bài ta có
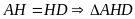 vuông cân tại H nên
vuông cân tại H nên
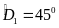
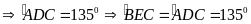 ,
do đó
,
do đó
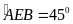 mà
mà
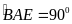 .
.
Suy ra
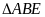 vuông cân tại A nên
vuông cân tại A nên
 .
.
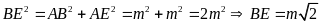 .
.
b) Ta có:

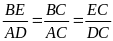 mà
mà
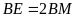 nên
nên
 mà
mà
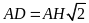 (
(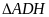 vuông cân tại H), nên
vuông cân tại H), nên
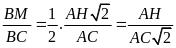 (1)
(1)
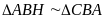
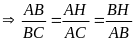
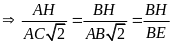 (2)
(2)
Từ (1) và
(2) suy ra

Do
đó
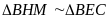 (c.g.c), suy ra:
(c.g.c), suy ra:
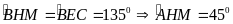 .
.
c) Vì AM
là tia phân giác của
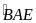 nên
nên
 mà
mà
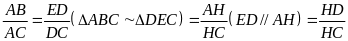
Do đó
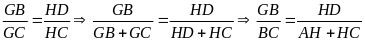 .
.
ĐỀ 12 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Bài 1. Cho biểu thức

a) Rút gọn P.
b) Tính
giá trị của P khi
 .
.
c) Tìm các giá trị nguyên của x để P nhận giá trị nguyên.
d) Tìm x
để
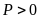 .
.
Bài 2
a) Chứng
minh rằng
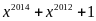 chia hết cho
chia hết cho
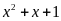 .
.
b) Tìm đa
thức A biết rằng
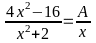 .
.
c) Tìm các
số nguyên dương x, y biết:
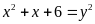 .
.
Bài 3. Cho các số nguyên a, b, c. Chứng minh rằng:
Nếu
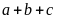 chia hết cho 30 thì
chia hết cho 30 thì
 chia hết cho 30.
chia hết cho 30.
Bài 4. Cho tam giác ABC cân tại A, H là trung điểm của BC. Gọi I là hình chiếu của của H lên AC và O là trung điểm của HI. Chứng minh:
a)
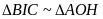 .
.
b)
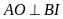 .
.
Bài 5. Cho
 .
Rút gọn biểu thức:
.
Rút gọn biểu thức:
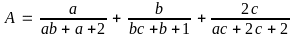
HƯỚNG DẪN
Bài 4

Cho tam giác ABC cân tại A, H là trung điểm của BC. Gọi I là hình chiếu của của H lên AC và O là trung điểm của HI. Chứng minh:
a)
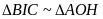 .
.
b)
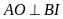 .
.
Kẻ
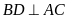 ,
ta có
,
ta có
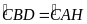 (cùng phụ với
(cùng phụ với
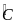 )
)
Do đó
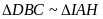 (g.g), suy ra
(g.g), suy ra
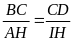
Ta có
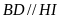 mà
mà
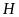 là trung điểm của BC nên I là trung điểm của DC.
là trung điểm của BC nên I là trung điểm của DC.
Do đó BI
và AO là hai đường trung tuyến của hai tam giác đồng
dạng DBC và EAH nên:
 .
.
Do đó
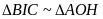 (c.c.c), suy ra
(c.c.c), suy ra
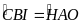
b) Từ
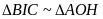 suy
ra
suy
ra
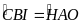 mà
mà
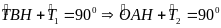
Suy ra
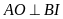 .
.
ĐỀ 13 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Bài 1. Cho
biểu thức
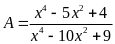
a) Rút gọn A.
b) Tìm x
để
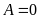 .
.
c) Tìm giá
trị của A khi
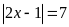 .
.
Bài 2
a) Phân
tích đa thức sau thành nhân tử
 .
.
b) Rút gọn
rồi tính giá tị của biểu thức
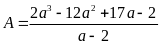
Biết rằng
a là nghiệm của phương tình:
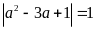
Bài 3. Cho
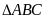 cân tại A, có
cân tại A, có
 ,
M là trung điểm của BC. Lấy D, E thuộc AB, AC sao cho
,
M là trung điểm của BC. Lấy D, E thuộc AB, AC sao cho
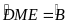 .
.
a) Chứng
minh
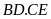 không đổi.
không đổi.
b) Chứng
minh DM là tia phân giác của
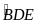 .
.
c) Tính
chu vi của tam giác AED nếu
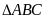 đều.
đều.
Bài 4. Cho a, b, c là độ dài ba cạnh của một tam giác.
Chứng
minh rằng nếu
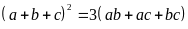 thì tam giác đó là tam giác đều.
thì tam giác đó là tam giác đều.
Bài 5. Cho
ba số x, y, z thỏa mãn điều kiện
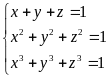
Tính giá
trị của biểu thức
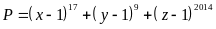 .
.
HƯỚNG DẪN
Bài 1. Ta
có
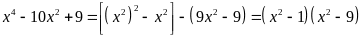
ĐKXĐ:
 ;
;
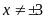 .
.
a)
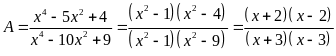
b)
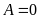
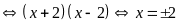 .
.
c)
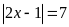

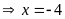 (vì
(vì
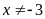 )
)
Với
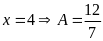 .
.
Bài 3
Cho
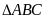 cân tại A, có
cân tại A, có
 ,
M là trung điểm của BC. Lấy D, E thuộc AB, AC sao cho
,
M là trung điểm của BC. Lấy D, E thuộc AB, AC sao cho
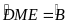 .
.
a) Chứng
minh
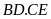 không đổi.
không đổi.
b) Chứng
minh DM là tia phân giác của
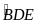 .
.
c) Tính
chu vi của tam giác AED nếu
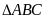 đều.
đều.
Hướng dẫn
a) Xét
 và
và
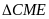 có:
có:
 (gt)
(gt)
 mà
mà
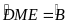 nên
nên
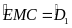
Do đó
 (g.g)
(g.g)
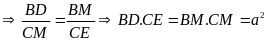
b)
ĐỀ 14 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1. (2,0 điểm)
a) Phân tích đa thức sau
thành nhân tử:
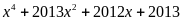 .
.
b) Rút gọn biểu thức
sau
 .
.
Câu 2. (2,0 điểm)
a) Giải phương trình sau:
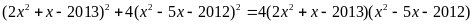
b) Chứng minh với mọi m,
n, p, q ta đều có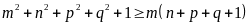
Câu 3. (2,0 điểm)
Tìm đa thức f(x) biết
rằng: f(x) chia cho
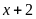 dư 10, f(x) chia cho
dư 10, f(x) chia cho
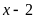 dư
24, f(x) chia cho
dư
24, f(x) chia cho
 được thương là
được thương là
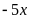 và còn dư.
và còn dư.
Câu 4. (3,0 điểm)
Cho hình vuông ABCD, trên cạnh AB lấy điểm E và trên cạnh AD lấy điểm F sao cho AE = AF. Vẽ AH vuông góc với BF (H thuộc BF), AH cắt DC và BC lần lượt tại hai điểm M, N.
a) Chứng minh rằng tứ giác AEMD là hình chữ nhật.
b) Biết
diện tích tam giác BCH gấp bốn lần diện tích tam giác
AEH. Chứng minh rằng
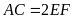 .
.
d) Chứng
minh rằng
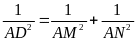 .
.
Câu 5. (1,0 điểm)
Câu
6. Cho
 là
ba số dương thoả mãn
là
ba số dương thoả mãn
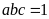 .
Chứng
minh rằng :
.
Chứng
minh rằng :
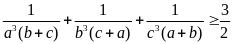 .
.
---------------Hết----------------
Cán bộ coi thi không giải thích gì thêm.
HƯỚNG DẪN CHẤM
BÀI THI CHỌN HỌC SINH GIỎI CẤP HUYỆN
Câu |
Hướng dẫn giải |
Điểm |
|
Câu 1 |
|
(2.0 điểm) |
|
1 (1.0 điểm) |
Ta có
|
0,25 |
|
|
0.25 |
||
|
0.25 |
||
Kết luận
|
0.25 |
||
2 (1.0 điểm) |
ĐK:
|
0.25 |
|
Ta có
|
|
||
|
0.25 |
||
|
0.25 |
||
|
0.25 |
||
Vậy
|
|
||
Câu 2 |
|
(2.0 điểm) |
|
1 (1.0 điểm) |
Đặt:
|
0.25 |
|
Phương trình đã cho trở thành:
|
0.25 |
||
Khi đó, ta có:
|
0.25 |
||
|
0.25 |
||
Vậy phương trình có
nghiệm duy nhất
|
|
||
2 (1.0 điểm) |
Ta có
|
0.25 |
|
|
0.25 |
||
Từ (1) và (2) ta có x < y < x+2 mà x, y nguyên suy ra y = x + 1 |
0.25 |
||
Thay y = x + 1 vào pt ban đầu và giải phương trình tìm được x = -1; từ đó tìm được hai cặp số (x, y) thỏa mãn bài toán là: (-1 ; 0)
|
0.25 |
||
Câu 3 |
|
(2,0 điểm) |
|
1 (1.0 điểm) |
Giả sử f(x) chia cho
Khi
đó:
|
0.25 |
|
Theo đề bài, ta có:
|
0.25 |
||
Do đó:
|
0.25 |
||
Vậy đa thức f(x) cần
tìm có dạng:
|
0.25 |
||
2 (1.0 điểm) |
Ta có:
Đặt: |
0.25 |
|
Khi đó, ta có:
|
0.25 |
||
|
0.25 |
||
|
0.25
|
||
|
0.25 |
||
Câu 4 |
|
(3,0 điểm) |
|
1 (1.0 điểm)
|
|
|
|
Ta có
AB = AD ( gt)
|
0.5
|
||
=> DM=AF, mà AF = AE (gt) Nên. AE = DM Lại có AE // DM ( vì AB // DC ) |
0.25 |
||
Suy ra tứ giác AEMD là hình bình hành Mặt
khác. |
|
||
Vậy tứ giác AEMD là hình chữ nhật |
0.25 |
||
2 (1.0 điểm)
|
Ta có
|
0.25 |
|
Lại
có
|
0.25 |
||
|
0.25 |
||
Do đó: BD = 2EF hay AC = 2EF (đpcm) |
0.25 |
||
3 (1.0 điểm) |
Do AD // CN (gt). Áp dụng hệ quả định lý ta lét, ta có:
|
0.25 |
|
Lại có: MC // AB ( gt). Áp dụng hệ quả định lý ta lét, ta có:
|
0.25 |
||
|
0.25 |
||
|
0.25 |
||
Câu 5 1,0 điểm |
|||
Câu 5: 1.0 điểm |
Trước
tiên ta chứng minh BĐT: Với
Dấu
“=” xảy ra
Thật
vậy, với a, b
Dấu
“=” xảy ra
Áp dụng bất đẳng thức (**) ta có
Dấu
“=” xảy ra
|
0.50 |
|
Ta
có:
Áp dụng bất đẳng thức (*) ta có
|
0.25 |
||
Hay
|
|
||
Mà
|
0.25 |
||
Vậy
|
|
||
|
Điểm toàn bài |
(10,0 điểm) |
|
ĐỀ 15 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Bài 1
a) Xác định các hằng số a, b sao cho:
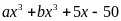 chia hết cho
chia hết cho
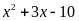
b) Tìm
nghiệm nguyên của phương trình sau:
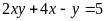
Bài 2
a) Chứng
minh rằng
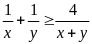 với
với
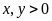 .
.
Chứng
minh bất đẳng thức sau:
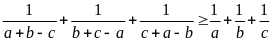 với a, b, c là độ dài ba cạnh của một tam giác.
với a, b, c là độ dài ba cạnh của một tam giác.
Bài 3. Cho
hình chữ nhật có
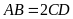 ,
gọi E, I lần lượt là trung điểm của AB, CD.
,
gọi E, I lần lượt là trung điểm của AB, CD.
Nối D với
E. Vẽ
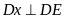 ,
tia Dx cắt tia đối của tia CB tại M. Trên tia đối của
tia CE lấy điểm K sao cho
,
tia Dx cắt tia đối của tia CB tại M. Trên tia đối của
tia CE lấy điểm K sao cho
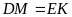 .
Gọi G là giao điểm của DK và EM.
.
Gọi G là giao điểm của DK và EM.
a) Tính
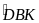 .
.
b) Gọi H là chân đường vuông góc hạ từ K xuống BM.
Chứng minh bốn điểm A, I, G, H cùng nằm trên một đường thẳng.
Bài 4. Cho
ba số thực khác 0 thỏa mãn điều kiện:
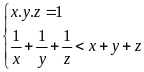
Chứng minh rằng có đúng một trong ba số x, y, z lớn hơn 1.
Bài 5.
Chứng minh rằng các số tự nhiên có dạng
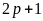 trong đó p là số nguyên tố, chỉ có một số là lập
phương của một số tự nhiên khác.
trong đó p là số nguyên tố, chỉ có một số là lập
phương của một số tự nhiên khác.
Bài 6. Cho a a, b, c là độ dài ba cạnh của một tam giác và chu vi 2p
Chứng minh rằng:
a)
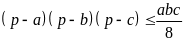
b)
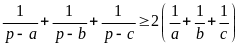
HƯỚNG DẪN
Bài 3.

a) Ta có:
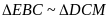 (g.g)
(g.g)
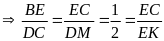
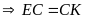 mà
mà
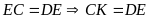
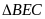 vuông cân
tại B nên
vuông cân
tại B nên
 ,
,
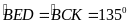
Do đó
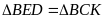 (c.g.c)
(c.g.c)
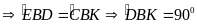
b) Ta có
tứ giác DEKM là hình chữ nhật nên
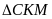 vuông cân tại M suy ra H là trung điểm của CM.
vuông cân tại M suy ra H là trung điểm của CM.
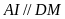 (cùng
vuông góc với DE),
(cùng
vuông góc với DE),
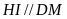 (tính chất đường trung bình) nên ba điểm A ; I, H
thẳng hàng.
(tính chất đường trung bình) nên ba điểm A ; I, H
thẳng hàng.
Các tam
giác CIH, CHK vuông cân tại C và H nên
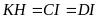 mà
mà
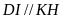 nên tứ giác DIKH là hình bình hành.
nên tứ giác DIKH là hình bình hành.
Lại có tứ giác DEKM là hình chữ nhật, do đó EM, DK, IH đồng quy tại G là trung điểm của DK.
Vậy
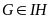 do đó bốn điểm A, I, G, H cùng nằm trên một đường
thẳng.
do đó bốn điểm A, I, G, H cùng nằm trên một đường
thẳng.
Bài 5
Chứng
minh rằng các số tự nhiên có dạng
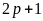 trong đó p là số nguyên tố, chỉ có một số là lập
phương của một
số tự nhiên khác.
trong đó p là số nguyên tố, chỉ có một số là lập
phương của một
số tự nhiên khác.
Hướng dẫn
Đặt
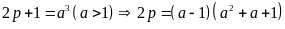
Vì p là số nguyên tố nên:
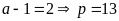 (thỏa
mãn)
(thỏa
mãn)
Hoặc
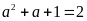 (vô lí) vì
(vô lí) vì
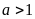
Vậy trong
các số tự nhiên có dạng
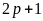 trong đó p là số nguyên tố, chỉ có một số là lập
phương của một số tự nhiên khác.
trong đó p là số nguyên tố, chỉ có một số là lập
phương của một số tự nhiên khác.
ĐỀ 16 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1 (4 điểm) Phân tích các đa thức sau thành nhân tử:
1)
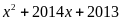
2)
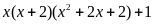
Câu 2 (4 điểm)
1) Tìm
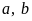 biết
biết
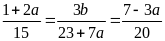
2) Tìm giá
trị nhỏ nhất của biểu thức
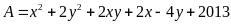
Câu 3 (4 điểm)
1) Cho
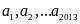 là các số tự nhiên có tổng bằng
là các số tự nhiên có tổng bằng
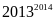 .
.
Chứng
minh rằng:
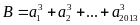 chia hết cho 3.
chia hết cho 3.
2) Cho
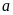 và
và
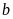 là các số tự nhiên thoả mãn
là các số tự nhiên thoả mãn
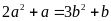 .
.
Chứng minh rằng:
 và
và
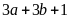 là các số chính phương.
là các số chính phương.
Câu 4 (6 điểm)
Cho tam giác ABC. Gọi I là một điểm di chuyển trên cạnh BC. Qua I, kẻ đường thẳng song song với cạnh AC cắt cạnh AB tại M. Qua I, kẻ đường thẳng song song với cạnh AB cắt cạnh AC tại N.
1) Gọi O là trung điểm của AI. Chứng minh rằng ba điểm M, O, N thẳng hàng.
2) Kẻ MH, NK, AD vuông góc với BC lần lượt tại H, K, D.
Chứng minh rằng MH + NK = AD.
3) Tìm vị trí của điểm I để MN song song với BC.
Câu 5 (2 điểm)
Cho
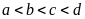 và
và
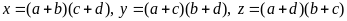 .
Sắp xếp theo thứ tự giảm dần của
.
Sắp xếp theo thứ tự giảm dần của
 .
.
.................................... Hết ......................................
Họ và tên thí sinh: ....................................................., Số báo danh: .....................
ĐÁP ÁN
Chú ý: Dưới đây là hướng dẫn cơ bản, bài làm của học sinh phải trình bày chi tiết. HS giải bằng nhiều cách khác nhau đúng vẫn cho điểm từng phần tương ứng. |
|||
Câu |
Ý |
Nội Dung |
Điểm |
1 |
1 |
|
0.5 |
|
1 |
||
|
0.5 |
||
2 |
|
0.5 |
|
|
0.5 |
||
|
0.5 |
||
|
0.5 |
||
2 |
1 |
Từ
|
0.5 |
|
0.5 |
||
Thay
|
0.5 |
||
Vậy
|
0.5 |
||
2 |
Ta có
|
0.5 |
|
|
0.5 |
||
Nhận
thấy với mọi x,y ta có
Suy
ra Dấu
“=” xảy ra khi
|
0.5
|
||
Vậy
Giá trị nhỏ nhất của A
là 2003 đạt được khi
|
0.5 |
||
3 |
1 |
Dễ
thấy
|
0.5 |
Xét
hiệu
|
0.5 |
||
Mà
|
0.5 |
||
Do vậy B chia hết cho 3. |
0.5 |
||
2 |
Từ
|
0.5 |
|
Cũng có
|
0.5 |
||
Gọi
|
0.5 |
||
|
0.5 |
||
4 |
|
|
|
1 |
Ta có
IM//AC, IN//AB
|
1 |
|
|
0.5 |
||
|
0.5 |
||
2
|
Kẻ OE vuông góc với BC. Chứng minh MHKN là hình thang vuông. |
0.5 |
|
Ta có O là trung điểm MN mà OE//MH//NK. Suy ra OE là đường trung bình của hình thang vuông MNKH nên MH + NK = 2OE (1) |
0.5 |
||
Xét
|
0.5 |
||
Từ (1) và (2) ta có MH + NK = AD (đpcm). |
0.5 |
||
3 |
Ta có
MN // BC khi và chỉ khi MN là đường trung bình của |
0.5 |
|
|
1 |
||
Vậy để MN song song với BC thì I là trung điểm BC |
0.5 |
||
5 |
|
Xét
hiệu
|
0.5 |
Vì
|
0.5 |
||
Xét
hiệu
|
0.5 |
||
Vì
Từ
(1) và (2) ta sắp xếp theo thứ tự giảm dần là
|
0.5 |
||
ĐỀ 17 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1. Cho phân thức
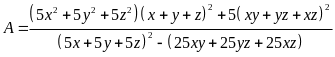
a) Tìm các giá trị của x, y, z để phân thức xác định
b) Rút gọn A
Câu 2
a) Tìm các giá trị của a để
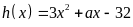 chia cho
chia cho
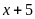 có số dư là 3
có số dư là 3
b) Giải phương trình nghiệm nguyên
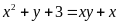
c) Phân tích đa thức
 thành nhân tử
thành nhân tử
Câu 3
a) Cho
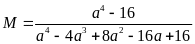 .
Tìm
.
Tìm
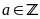 để
để
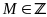
b) Biết
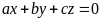 và
và
 .
.
Tính
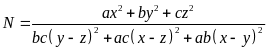
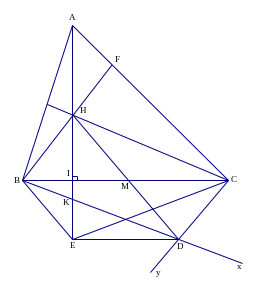
Câu 4. Cho tam giác ABC nhọn, trực tâm H.
Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ các
tia
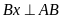 ,
,
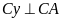 chúng cắt nhau tại D.
chúng cắt nhau tại D.
a) Tứ giác BHCD là hình gì? Vì sao?
b) Gọi E là điểm sao cho BC là đường trung trực của EH. Chứng minh tứ giác BCDE là hình thang cân.
c) BD cắt EH tại K. Tam giác ABC phải có thêm điều kiện gì để tứ giác HCDK là hình thang cân
Câu 5. Cho
 .
Chứng minh rằng
.
Chứng minh rằng
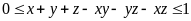
HƯỚNG DẪN
Câu 1
a) Ta có
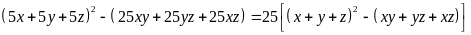
Xét


Để phân thức xác định thì x, y, z không đồng thời bằng 0
b) Đặt
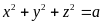 và
và
 thì
thì
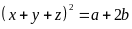
Khi đó
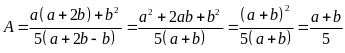
Vậy

Câu 4
a) HS tự làm
b) Gọi I là giao điểm của AE và BC, K là giao điểm của EH và BD
Ta có
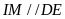 nên
nên
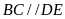 ,
do đó tứ giác BCDE là hình thang
,
do đó tứ giác BCDE là hình thang
Lại có
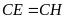 mà
mà
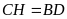 nên
nên
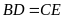 ,
vậy tứ giác BDCE là hình thang cân
,
vậy tứ giác BDCE là hình thang cân
c) BH cắt AC tại F, ta có
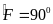
Hình thang HKDC là hình thang cân
 (vì
(vì
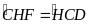 (so le trong))
(so le trong))
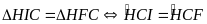
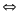 CH
là phân giác của góc ACB
CH
là phân giác của góc ACB
 cân tại C.
cân tại C.
Vậy HKDC là hình thang cân khi và chỉ khi
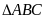 là tam giác cân tại C.
là tam giác cân tại C.
Câu 5
Từ
 suy ra
suy ra
 ;
;
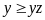 và
và
 nên
nên
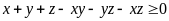 (1)
(1)
Xét
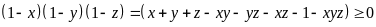
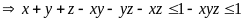 (2)
(2)
Từ (1) và (2) suy ra
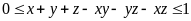
ĐỀ 18 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
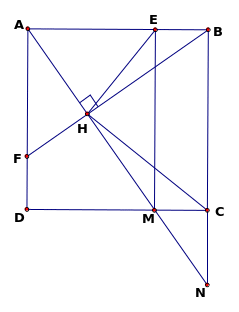
Câu 1. Phân tích các đa thức sau thành nhân tử
a)
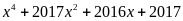
b)
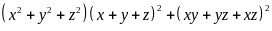
Câu 2
a) Một số điện thoại có 10 chữ số là
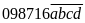 .
Hãy tìm bốn số cuối của bốn số điện thoại đó,
biết rằng bốn số này tạo thành một số chính phương
và nếu ta thêm vào mỗi chữ số của nó một đơn vị
thì cũng được một số chính phương.
.
Hãy tìm bốn số cuối của bốn số điện thoại đó,
biết rằng bốn số này tạo thành một số chính phương
và nếu ta thêm vào mỗi chữ số của nó một đơn vị
thì cũng được một số chính phương.
b) Chứng minh rằng với
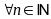 ,
,
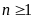 ,
ta có
,
ta có
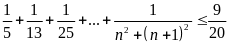
Câu 3
a) Chứng minh rằng với
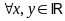 ,
ta luôn có
,
ta luôn có

b) Cho
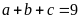 và
và
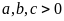 .
Tìm giá trị nhỏ nhất của biểu thức
.
Tìm giá trị nhỏ nhất của biểu thức
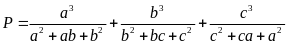
Câu 4
a) Tìm các số nguyên x, y, z biết
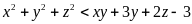
b) Phân tích đa thức
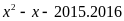
Câu 5
1) Cho tam giác vuông ABC có độ dài các cạnh góc vuông AB=6cm, AC=8cm. M là điểm di chuyển trên cạnh huyền BC. Gọi D và E là chân các đường vuông góc kẻ từ M đến AB và AC. Khi đó tứ giác ADME có thể đạt được diện tích lớn nhất là bao nhiêu?
2) Cho hình vuông ABCD và một tứ giác MNPQ có bốn đỉnh thuộc bốn cạnh của hình vuông.
Chứng minh rằng:
a)
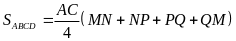
b) Xác định vị trí của M, N, P, Q để chu vi tứ giác MNPQ nhỏ nhất
c) Xác định vị trí của M, N, P, Q để diện tích tứ giác MNPQ nhỏ nhất
HƯỚNG DẪN
Câu 1
b) Đặt
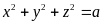 ;
;
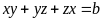 ,
ta có
,
ta có
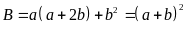
Câu 2
a) Theo đề bài ta có:
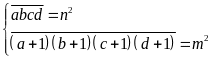 (
( )
)
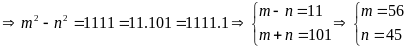
Vậy số điện thoại cần tìm là 0987162025
b) Ta có
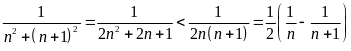
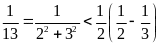
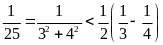
………
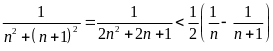
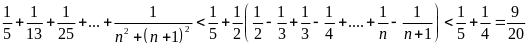
Câu 4
a)
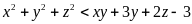

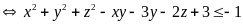 (vì x, y, z là các số nguyên)
(vì x, y, z là các số nguyên)
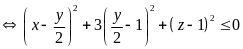
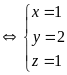
b)
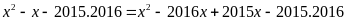
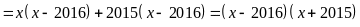
Câu 5
1)
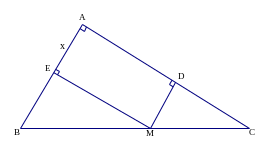
Đặt
 (
( )
)
Ta có

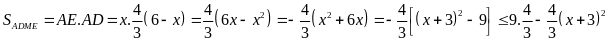 Vậy
Vậy
 là trung điểm của BC
là trung điểm của BC
2)
a) Gọi I, J, K lần lượt là trung điểm của QN, MN, PQ ta có
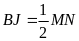 ;
;
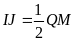 ;
;
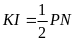 ;
;
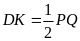
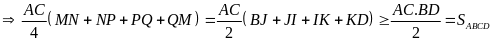
b) Theo phần a) chu vi tứ giác MNPQ đạt
giá trị nhỏ nhất khi đường gấp khúc BJIKD trùng với
đoạn BD, tức là khi
 và
và
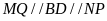 lúc đó tứ giác MNPQ là hình chữ nhật.
lúc đó tứ giác MNPQ là hình chữ nhật.
Vậy với mọi hình chữ nhật nội tiếp hình vuông đã cho đều có chu vi bằng nhau và chu vi đó nhỏ nhất so với chu vi tất cả các tứ giác nội tiếp hình vuông này.
c)

Từ các đỉnh M, N, P, Q ta dựng các đường thẳng song song với các cạnh của hình vuông. Các đường thẳng đó hoặc trùng nhau hoặc song song.
Nếu chúng song song từng đôi thì giao điểm của chúng sẽ tạo thành hình chữ nhật. Ta có
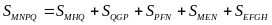
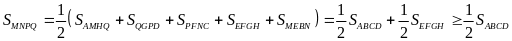
Do đó
 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất
 hoặc
hoặc
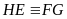
Vậy tứ giác nội tiếp hình vuông có diện tích nhỏ nhất khi và chỉ khi có ít nhất một trong hai đường chéo của nó song song với cạnh của hình vuông
ĐỀ 19 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1. Cho a, b là bình phương của hai số nguyên lẻ liên
tiếp. Chứng minh rằng
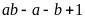 chia hết cho 48.
chia hết cho 48.
Câu 2
a) Giải phương trình:

b) Cho các số a, b, c, d thỏa mãn
 .
Tính giá trị của biểu thức
.
Tính giá trị của biểu thức
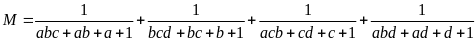
Câu 3. Cho đa thức
 thỏa mãn khi chia cho
thỏa mãn khi chia cho
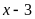 thì dư
thì dư
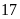 ;
khi chia cho
;
khi chia cho
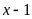 dư 3. tìm dư của phép chia
dư 3. tìm dư của phép chia
 cho
cho
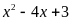
Câu 4. Cho tam giác ABC nhọn có các đường
cao
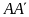 ;
;
 ;
;
 ,
trực tâm H
,
trực tâm H
a) Tính tổng
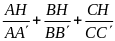
b) Gọi AI là phân giác của tam giác ABC;
IM, IN theo thứ tự là phân giác của các góc AIC; AIB (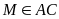 ,
,
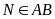 ).
Chứng minh
).
Chứng minh

c) Tam giác ABC phải thỏa mãn điều kiện
gì thì biểu thức
 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất
Câu 5. Cho x, y, z là các số dương thỏa
mãn
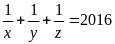 .
.
Tìm giá trị lớn nhất của biểu thức
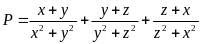
HƯỚNG DẪN
Câu 1
Ta có
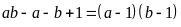
Vì a, b là bình phương của hai số nguyên lẻ liên tiếp
nên
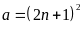 ,
,
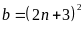 ,
(
,
(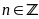 ),
suy ra
),
suy ra
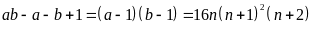
Vì
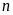 ,
,
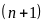 ,
,
 là tích của ba số nguyên liên tiếp nên
là tích của ba số nguyên liên tiếp nên
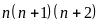 chia hết cho 3, mà
chia hết cho 3, mà
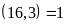 nên
nên
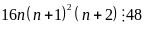 nên
nên
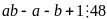 .
.
Câu 2
a) Đặt
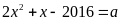 ;
;
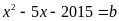 ,
ta có
,
ta có
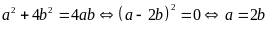 ,
từ đó tìm ra x
,
từ đó tìm ra x
Câu 3
Vì đa thức chia là
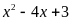 có bậc hai nên đa thức dư có dạng
có bậc hai nên đa thức dư có dạng
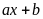
Ta có
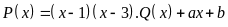
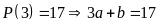 và
và
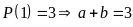
Do đó
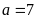 ;
;
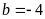 nên đa thức dư có dạng
nên đa thức dư có dạng
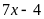
Câu 4
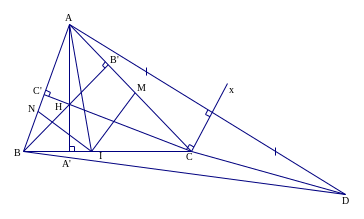
a) Ta có
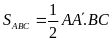 ;
;
 ;
;

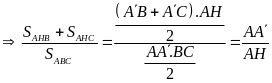
Chứng minh tương tự ta có:
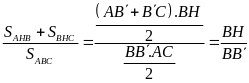 ;
;


b) Theo tính chất đường phân giác trong tam giác ta có:
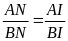 ;
;
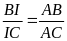 ;
;
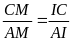 ,
từ đó suy ra
,
từ đó suy ra
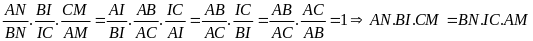
c) Vẽ
 ,
gọi D là điểm đối xứng với A qua Cx
,
gọi D là điểm đối xứng với A qua Cx
Ta có tam giác BAD vuông tại A và
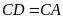 ;
;
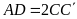
Xét ba điểm B, C, D, ta có
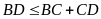
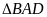 vuông tại A nên
vuông tại A nên
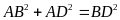

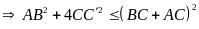

Chứng minh tương tự ta có:
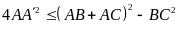

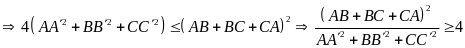
Đẳng thức xảy ra
 đều
đều
Câu 5
Áp dụng các bất đẳng thức
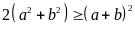 ;
;
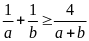
Ta có
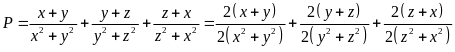


Vậy
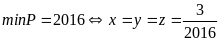
ĐỀ 20 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 8 Thời gian: 150 phút |
Câu 1. Chứng minh rằng:
a) Nếu tổng của hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 9.
b) Tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.
Câu 2. Cho biểu thức

a) Rút gọn biểu thức B
b) Tính giá trị của biểu thức B tại
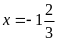
c) Tìm giá trị của x để

Câu 3
a) Giải phương trình
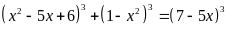
b) Cho
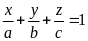 và
và
 .
Chứng minh rằng
.
Chứng minh rằng
 .
.
Câu 4. Cho hình chữ nhật ABCD. Trên đường chéo BD lấy điểm P, gọi M là điểm đối xứng của điểm C qua P.
a) Tứ giác AMDB là hình gì? Tại sao?
b) Gọi E và F lần lượt là hình chiếu của điểm M
lên AB và AD. Chứng minh
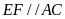 và ba điểm E, F, P thẳng hàng.
và ba điểm E, F, P thẳng hàng.
c) Chứng minh rằng tỉ số các cạnh của hình chữ nhật MEAF không phụ thuộc vào vị trí của điểm P.
d) Giả sử
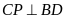 và
và
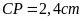 ,
,
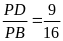 .
Tính độ dài các cạnh của hình chữ nhật ABCD.
.
Tính độ dài các cạnh của hình chữ nhật ABCD.
Câu 5. Tìm tất cả các số nguyên dương x, y, z thoả mãn đồng thời các điều kiện:
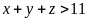 và
và
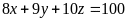
HD CHẤM THI Môn: Toán
Câu 1: (4 điểm)
a. (2,0) |
Gọi 2 số phải tìm là a và b, ta có a + b chia hết cho 3. 0,25
Ta có
a3
+
b3
=
(a + b)(a2
–
ab + b2)
= (a + b)
=
(a + b) Vì a + b chia hết cho 3 nên (a + b)2 - 3ab chia hết cho 3; Do
vậy (a + b) |
0,25 0,5 0,25 0,5 0,5 |
b. (2,0) |
Gọi 4
số tự nhiên, liên tiêp đó là: n, n + 1, n + 2, n + 3 (n
Ta có n(n + 1)(n + 2)(n + 3) + 1 = n.(n + 3(n + 1)(n + 2) + 1 = (n2 + 3n)( n2 + 3n + 2) + 1 (*) Đặt
n2
+ 3n = t (t
= (n2 + 3n + 1)2 Vì
n
|
0,25 0,25 0,5 0,25 0,25
0,5 |
Câu 2 ( 4,0 điểm ) .
a, ( 2 điểm ) Với x khác -1 và 1 thì:
A
=
=
=
|
0,5 1,0
0,5 |
|
b,
(1 điểm) Tại x =
|
0,25 |
|
=
|
0,75 |
|
c, (1
điểm) Với x khác -1 và 1 thì B < 0 khi và chỉ khi
|
0,25 |
|
Vì
KL: B < 0 khi và chỉ khi x > 1 |
0,5 0,25 |
|
Câu 3: (4,0 điểm)
a. (2,0) |
Đặt x2 - 5x + 6 = a, 1 - x2 = b thì a + b = 7 - 5x Phương trình trở thành a3 + b3 = (a + b)3 Biến đổi thành ab(a + b) = 0 <=> a = 0 hoặc b = 0 hoặc a + b = 0 Từ
đó tìm được S =
|
0,5
0,5 1,0 |
b (2,0)
|
Từ :
Ta có :
|
0,5
0,5
0,5
0,5 |
Câu 4. (6,0 điểm):
|
0,25 |
a) Gọi O là giao điểm 2 đường chéo của hình chữ nhật ABCD. PO là đường trung bình của tam giác CAM (... ) AM//PO
|
1,0 |
b) Do AM //BD nên góc OBA = góc MAE (đồng vị) Tam giác AOB cân ở O nên góc OBA = góc OAB Gọi I là giao điểm 2 đường chéo của hình chữ nhật AEMF thì tam giác AIE cân ở I nên góc IAE = góc IEA. Từ chứng minh trên : có góc FEA = góc OAB, do đó EF//AC (1) Mặt khác IP là đường trung bình của tam giác MAC nên IP // AC (2) Từ (1) và (2) suy ra ba điểm E, F, P thẳng hàng. |
1,75 |
c) Chứng minh
|
1,0 |
d) Nếu
Nếu
do đó CP2 = PB.PD hay (2,4)2 = 9.16 k2 => k = 0,2 PD = 9k = 1,8(cm); PB = 16k = 3,2 (cm => BD = 5 (cm) C/m BC2 = BP.BD = 16 do đó BC = 4 (cm); CD = 3 (cm) |
2,0 |
Câu 5. (2,0 điểm)
Ta có:
8x + 8y + 8z < 8x + 9y + 10z = 100 => x + y + z <
cùng với giả thiết, có 11 < x + y + z < 13, nhưng x + y + z Z => x + y + z = 12 Ta có hệ: x + y + z = 12 (1); 8x + 9y + 10z = 100 (2). Nhân 2 vế của (1) với 8 rồi trừ vế-vế của (2) cho (1), được: y + 2z = 4 (3) Từ (3) suy ra z = 1 (vì nếu z ≥ 2 thì do y ≥ 1 => y + 2z ≥ 4, mâu thuẫn) Với z = 1, tìm được y = 2 và x = 9. Thử lại, thấy đúng. Vậy có duy nhất bộ x = 9, y = 2 và z = 1 thoả mãn. |
0,5
0,5 0,25 0,25 0,25 0,25 |
Ngoài 20 Đề Thi HSG Toán 8 Có Lời Giải thì các đề thi trong chương trình lớp 8 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm









 1
1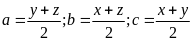
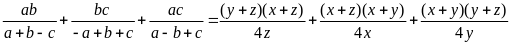
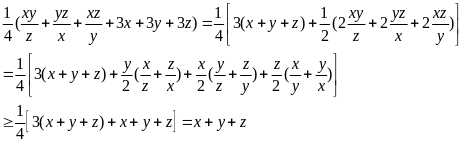
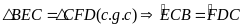 mà
mà
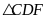 vuông tại C
vuông tại C
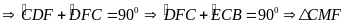 vuông tại M
vuông tại M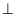 DF.
DF.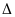 MAD có AN vừa là đường cao vừa là trung tuyến
MAD có AN vừa là đường cao vừa là trung tuyến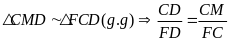
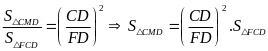
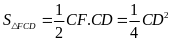


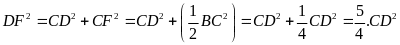

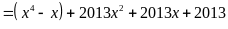
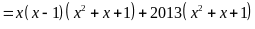
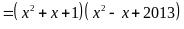
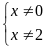
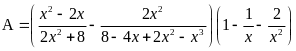
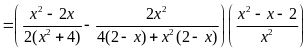

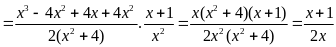
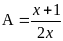 với
với


 .
. .
.

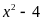 được thương là
được thương là
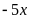 và còn dư là
và còn dư là
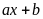 .
.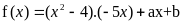
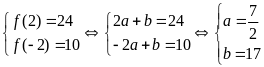
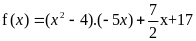


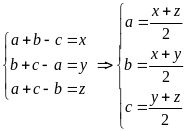
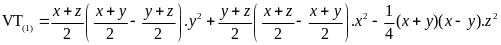
 (đpcm)
(đpcm)
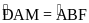 (cùng
phụ
(cùng
phụ
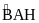 )
) (ABCD là hình vuông)
(ABCD là hình vuông)

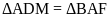 (g.c.g)
(g.c.g)
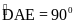 (gt)
(gt)
 (g.g)
(g.g)
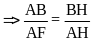 hay
hay
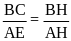 ( AB=BC, AE=AF)
( AB=BC, AE=AF)
 (cùng phụ
(cùng phụ
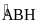 )
)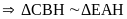 (c.g.c)
(c.g.c)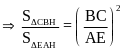 ,
mà
,
mà
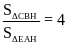 (gt)
(gt)
 nên BC2
= (2AE)2
nên BC2
= (2AE)2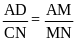
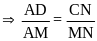
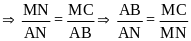 hay
hay
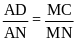
 (Pytago)
(Pytago)
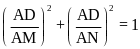
 (đpcm)
(đpcm)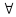
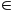
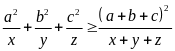
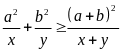
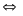
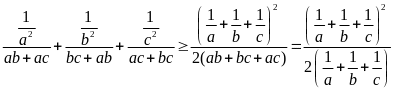 (Vì
(Vì
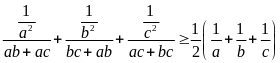
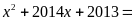
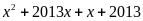
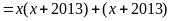
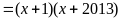
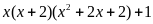
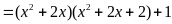
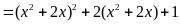
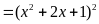
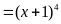
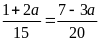
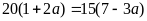
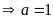

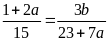
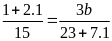
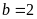
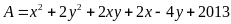
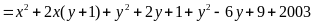

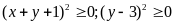
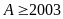
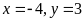
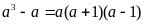

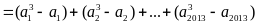
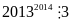
 có
có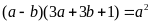
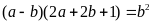 .
Suy ra
.
Suy ra

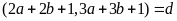 .
Chứng minh được d=1
.
Chứng minh được d=1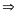
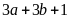


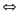

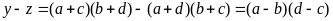

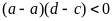
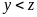
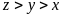
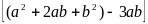




 =
=
 thỡ A =
thỡ A =
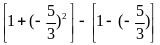

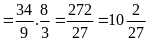
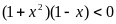

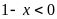
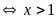
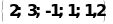

 ayz
+ bxz + cxy = 0
ayz
+ bxz + cxy = 0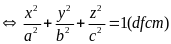
 Tứ giác AMDB là hình
thang.
Tứ giác AMDB là hình
thang.
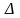 MAF
~
MAF
~
 không đổi.
không đổi.
 thì
thì
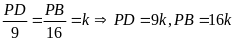
 thì
thì