Cách Giải Toán 6 Tập 2 Bài 1 Phép Thử Nghiệm Sự Kiện Chân Trời Sáng Tạo
>>> Mọi người cũng quan tâm:
Cách Giải Toán 6 Tập 2 Bài 1 Phép Thử Nghiệm Sự Kiện Chân Trời Sáng Tạo – Toán 6 Chân Trời Sáng Tạo là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
Chương 9. MỘT SỐ YẾU TỐ XÁC XUẤT
§ 1: PHÉP THỬ NGHIỆM – SỰ KIỆN
A. KIẾN THỨC CẦN NHỚ
- Trong các trò chơi (thí nghiệm) tung đồng xu, bốc thăm, gieo xúc xắc, quay sổ số,..., mỗi lần tung đồng xu, bốc thăm, gieo xúc xắc hay quay xổ số được gọi là một phép thử nghiệm.
- Khi thực hiện các thử nghiệm (trò chơi, thí nghiệm), ta rất khó để dự đoán trước chính xác kết quả của mỗi phép thử nghiệm đó. Tuy nhiên ta có thể liệt kê được tập hợp tất cả các kết quả có thể xảy ra của phép thử nghiệm đó.
- Khi thực hiện phép thử nghiệm, có những sự kiện chắc chắn xảy ra, có những sự kiện không thể xảy ra và cũng có những sự kiện có thể xảy ra.
B. BÀI TẬP CÓ HƯỚNG DẪN.
DẠNG 1: Dạng toán tung đồng xu, gieo xúc xắc.
Bài 1. Hai bạn Thái và An mỗi người tung một đồng xu. Hãy liệt kê tất cả các kết quả có thể xảy ra.
|
|
Hướng dẫn:
Có thể liệt kê trực tiếp hoặc dùng bảng hoặc dùng kí hiệu để liệt kê kết quả.
Lưu ý:
Thái tung đồng xu thì có thể là mặt sấp hoặc mặt ngửa, An tung đồng xu cũng có thể là mặt sấp hoặc mặt ngửa.
Bài 2. Gieo một con xúc xắc 6 mặt cân đối. Hãy đánh giá xem các sự kiện sau là chắc chắn, không thể hay có thể xảy ra. a) Mặt xuất hiện có số chấm chia hết cho 7. b) Mặt xuất hiện có số chấm nhỏ hơn 10. c) Mặt xuất hiện có số chấm lớn hơn 5. |
|
Hướng dẫn:
Số chấm trên xúc xắc chỉ từ 1 đến 6 chấm.
DẠNG 2: Dạng toán lựa chọn chọn đồ vật, ngày tháng,...
Bài 3. Hộp bút của Thảo có ba đồ dùng học tập gồm 1 bút máy, 1 bút chì, 1 bút bi. Thảo lấy ra một dụng cụ học tập từ hộp bút. Hãy đánh giá xem các sự kiện sau là chắc chắn, không thể hay có thể xảy ra. a) Thảo lấy được một cái bút. b) Thảo lấy được một cái thước kẻ. c) Thảo lấy được một cái bút bi. |
|
Hướng dẫn:
Vật dụng mà Thảo lấy ra có là vật dụng trong hộp bút đã được liệt kê ra hay không?
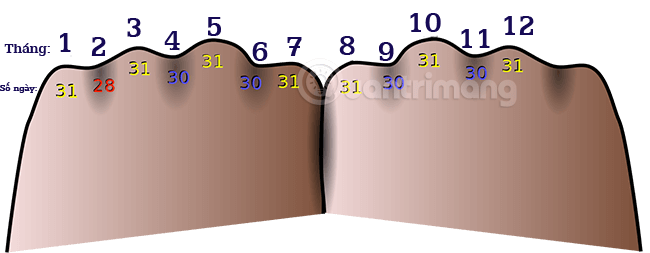
Bài 4. Để biết được tháng nào trong năm có 30 ngày, 31 ngày hay 28, 29 ngày. Đầu tiên bạn hãy nắm hai bàn tay lại và úp xuống cạnh nhau (như hình). Hãy đếm các khớp lần lượt từ trái qua phải theo thứ tự từ 1 đến 12 tương đương với 12 tháng. Khớp nhô lên đầu tiên bên trái sẽ là tháng 1, lõm xuống là tháng 2 cứ như thế cho hết các khớp trên bàn tay (bỏ qua khớp các ngón cái). Sau khi đếm xong nếu tháng nào nhô lên thì tháng đó sẽ có 31 ngày. Và ngược lại, tháng nào nằm lõm xuống sẽ là 30 ngày. Riêng tháng 2 tất cả các năm chỉ có 28 hoặc 29 ngày (năm nhuận có 29 ngày, 4 năm sẽ có 1 năm nhuận). Các sự kiện sau đây là chắc chắn, không thể hay có thể xảy ra?
a) Chọn được 5 tháng có đúng 30 ngày. b) Luôn chọn được tháng có 29 ngày trở lên. c) Chọn ra một tháng thì số ngày của tháng đó không vượt quá 31 ngày. |
|
Hướng dẫn:
a) Xét xem số tháng có đúng 30 ngày là bao nhiêu tháng?
b) Có năm nào tháng 2 có 29 ngày hay không?
c) Xem số ngày nhiều nhất các tháng trong năm.
DẠNG 3: Dạng khác
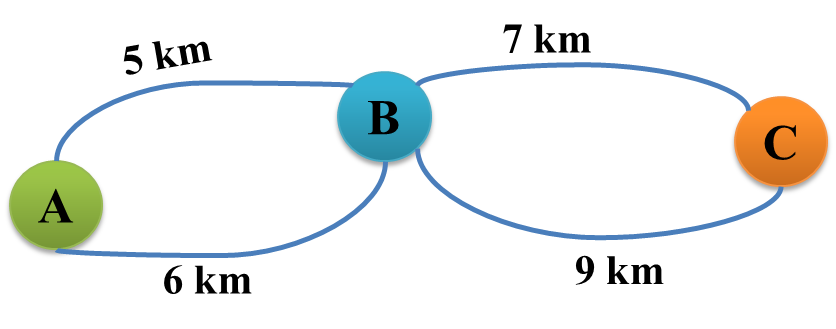
Bài 5. Có các tuyến đường với độ dài như hình vẽ để nối các điểm du lịch A, B và C. Bạn Dương đi từ A qua B rồi đến C. Hãy đánh giá xem các sự kiện sau là chắc chắn, có thể hay không thể xảy ra?
a) Quãng đường Dương đi không vượt quá 15 km b) Quãng đường Dương đi dài 11 km c) Quãng đường Dương đi dài 14 km |
|
Hướng dẫn:
a) Xem tổng quãng đường dài nhất từ A đến B và từ B đến C có vượt qua 15 km hay không?
b) Xem tổng quãng đường ngắn nhất từ A đến B và từ B đến C có bằng 11 km hay không?
c) Xét xem có tổng quãng đường từ A đến B và từ B đến C nào bằng 14 km hay không?
Bài 6. Một hộp đựng 10 thẻ được đánh số từ 1 đến 10. Chọn và lấy ra 3 thẻ. Hãy đánh giá xem các sự kiện sau là chắc chắn, có thể hay không thể xảy ra? a) Số trên 3 thẻ được lấy ra đều là số nguyên tố. b) Số trên 3 thẻ được lấy ra đều chia hết cho 5. c) Tích ba số trên 3 thẻ được lấy ra không nhỏ hơn 6. |
|
Hướng dẫn:
a) Viết ra các số nguyên tố nằm trong khoảng từ 1 đến 10 và xem có từ 3 số nguyên tố trở lên hay không?
b) Từ 1 đến 10 có bao nhiêu số chia hết cho 5.
c) Tính tích của 3 số nhỏ nhất và so sánh với 6.
C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.
Bài 7. Trong hộp có 4 quả bóng xanh, 3 quả bóng đỏ và 1 quả bóng vàng. Phương lấy ra 5 quả bóng từ hộp. Hỏi các sự kiện sau là chắc chắn, không thể hay có thể xảy ra? a) 5 quả bóng lấy ra có cùng màu. b) Có ít nhất 1 bóng xanh trong 5 quả bóng lấy ra. c) 5 quả bóng lấy ra có đủ ba màu xanh, đỏ và vàng. |
|
Đáp số:
a) Không thể xảy ra.
b) Chắc chắn xảy ra.
c) Có thể xảy ra.
Bài 8. Hộp bút của Ngọc có 1 cái bút mực, 1 cái bút chì và 1 cái thước kẻ. Ngọc lấy ra hai dụng cụ học tập từ hộp. Hỏi các sự kiện sau là chắc chắn, không thể hay có thể xảy ra? a) Ngọc lấy được 1 cái bút và 1 cái thước kẻ. b) Ngọc lấy được ít nhất 1 cái bút. c) Ngọc lấy được 2 cái thước kẻ. |
|
Đáp số:
a) Có thể xảy ra.
b) Chắc chắn xảy ra.
c) Không thể xảy ra.
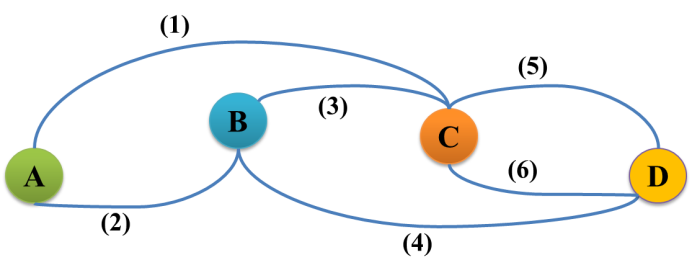
Bài 9. Bạn Dũng muốn đi từ tỉnh A đến tỉnh D thì phải đi qua các tỉnh B, C (không nhất thiết phải đi qua cả tỉnh B và tỉnh C) các tuyến đường được đánh số như hình vẽ để nối các tỉnh A, B, C và D. Em hãy liệt kê tất cả các cách bạn Dũng có thể đi từ tỉnh A đến tỉnh D?
|
Đáp số:
Các cách bạn Dũng có thể đi: {(1)(5); (1)(6); (2)(4); (2)(3)(5); (2)(3)(6)}
Bài 10. Gieo một con xúc xắc có 6 mặt cân đối 2 lần. Hãy liệt kê tất cả các kết quả có thể xảy ra về số chấm xuất hiện trên mặt xúc xắc thỏa điều kiện sau: a) Lần 1 là số chẵn, lần 2 là số lẻ. b) Lần 1 là số nguyên tố, lần 2 là số chẵn. c) Cả 2 lần đều là số chia hết cho 3. |
|
Đáp số:
a) {21; 23; 25; 41; 43; 45; 61; 63; 65}
b) {22; 24; 26; 32; 34; 36; 52; 54; 56}
c) {33; 36; 63; 66}
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Tung một đồng tiền và gieo một con xúc xắc có 6 mặt cân đối. Có tất cả bao nhiêu kết quả có thể xảy ra?
|
|
A. 24 B. 12 C. 6 D. 8
Câu 2. Trong các thí nghiệm sau. Đâu không phải là một phép thử nghiệm?
|
|
|
|
A. Tung một đồng tiền để xem là mặt sấp hay mặt ngửa.
B. Gieo một con xúc xắc để biết số chấm xuất hiện trên con xúc xắc.
C. Chọn lần lượt từng viên bi trong hộp để đếm xem có bao nhiêu viên bi trong hộp.
D. Chọn ra một bạn trong lớp để xem bạn đó sinh vào tháng mấy.
Câu 3. Lớp 6A có 5 bạn giỏi môn Toán, 4 bạn giỏi môn Văn và 3 bạn giỏi môn Tiếng Anh. Giáo viên chủ nhiệm chọn ra 4 bạn để tham gia vào câu lạc bộ học sinh giỏi của trường. Sự kiện nào sau đây là không thể xảy ra?
|
A. Những bạn được chọn có đủ cả 3 môn Toán, Văn, Tiếng Anh
B. Tất cả các bạn được chọn đều giỏi môn Toán.
C. Tất cả các bạn được chọn đều giỏi môn Văn.
D. Tất cả các bạn được chọn đều giỏi môn Tiếng Anh.
Câu 4. Một hộp đựng 20 thẻ, được đánh số từ 1 đến 20. Chọn ra 3 thẻ. Có bao nhiêu kết quả có thể xảy ra để tổng số trên 3 thẻ không vượt quá 8. A. 2 B. 3 C. 4 D. 5 |
|
|
Câu 5. Trong hộp có 3 viên bi đỏ, 4 viên bi xanh và 4 viên bi vàng. Bạn Tiên lấy ra 5 viên bi. Sự kiện nào sau đây là chắc chắn xảy ra? A. 5 viên bi lấy ra có ít nhất 2 màu. B. 5 viên bi lấy ra có đủ 3 màu. C. Tất cả 5 viên bi đều là màu vàng. D. Luôn có viên bi màu đỏ. |
|
|
Đáp số:
Câu 1. Chọn B
Câu 2. Chọn C
Câu 3. Chọn D
Câu 4. Chọn C
Câu 5. Chọn A
Ngoài Cách Giải Toán 6 Tập 2 Bài 1 Phép Thử Nghiệm Sự Kiện Chân Trời Sáng Tạo – Toán 6 Chân Trời Sáng Tạo thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Phương pháp giải toán được trình bày một cách chi tiết và dễ hiểu, giúp bạn nắm vững các bước cần thiết để giải quyết bài toán. Bạn sẽ học cách xác định không gian mẫu và sự kiện, tính toán xác suất sự kiện dựa trên tỉ lệ số phần tử, áp dụng các công thức và quy tắc trong xác suất.
Ngoài ra, sách cũng cung cấp các bài tập thực hành và ví dụ minh hoạ giúp bạn nắm vững kiến thức và rèn kỹ năng giải toán. Đáp án chi tiết và lời giải sẽ giúp bạn kiểm tra và hiểu rõ hơn về quy trình giải quyết bài toán. Hãy sử dụng tài liệu này để nâng cao khả năng giải toán và phát triển kỹ năng xác suất của mình. Chúc các bạn thành công trong việc học tập và giải quyết các bài toán thú vị!
>>> Bài viết có liên quan