Đề Cương Ôn Tập HK2 Toán 7 Năm 2021-2022 Có Phân Dạng
Có thể bạn quan tâm
| Kế Hoạch Giảng Dạy Môn Địa Lí Lớp 7 |
Đề Cương Ôn Tập HK2 Toán 7 Năm 2021-2022 Có Phân Dạng – Toán 7 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II
MÔN: TOÁN 7
I. ĐẠI SỐ
A.KIẾN THỨC CƠ BẢN:
Số liệu thống kê, tần số.
Bảng tần số các giá trị của dấu hiệu
Biểu đồ
Số trung bình cộng, Mốt của dấu hiệu.
Biểu thức đại số.
Đơn thức, bậc của đơn thức.
Đơn thức đồng dạng, quy tắc công (trừ) đơn thức đồng dạng.
Đa thức, cộng trừ đa thức
Đa thức một biến, quy tắc cộng (trừ) đa thức một biến
Nghiệm của đa thức một biến.
B. CÁC DẠNG BÀI TẬP CƠ BẢN:
* Dạng 1: Thu gọn biểu thức đại số:
Thu gọn đơn thức, tìm bậc, hệ số của đơn thức.
Phương pháp:
B1: Dùng qui tắc nhân đơn thức để thu gọn.
B2: Xác định hệ số, bậc của đơn thức đã thu gọn.
Bài tập áp dụng : Thu gọn đơn thức, tìm bậc, hệ số.
A
=
 ;
B =
;
B =
![]()
Thu gọn đa thöùc, tìm bậc của đa thức.
Phương pháp:
B1: nhóm các hạng tử đồng dạng, tính cộng, trừ các hạng tử đồng dạng ( thu gọn đa thức).
B2: bậc của đa thức đã là bậc của hạng tử có bậc cao nhất của đa thức đó.
Bài tập áp dụng : Thu gọn đa thức, tìm bậc của đa thức.
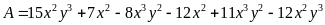
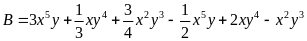
C= 5xy – 3,5y2 - 2 xy + 1,3 xy + 3x -2y;
D
=
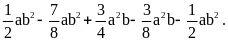
E=
2 -8b2+
5a2b + 5c2 – 3b2 + 4c2.
-8b2+
5a2b + 5c2 – 3b2 + 4c2.
* Dạng 2: Tính giá trị biểu thức đại số :
Phương pháp :
B1: Thu gọn các biểu thức đại số.
B2: Thay giá trị cho trước của biến vào biểu thức đại số.
B3: Tính giá trị biểu thức số.
Bài tập áp dụng :
Bài 1 : Tính giá trị biểu thức
a/.
A = 3x3
y + 6x2y2
+ 3xy3
tại
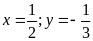 b/.
B = x2
y2 +
xy + x3
+ y3
tại x = –1; y = 3
b/.
B = x2
y2 +
xy + x3
+ y3
tại x = –1; y = 3
c.
A = 2x2
-
 tại x =
2 ; y = 9. d. B =
tại x =
2 ; y = 9. d. B =
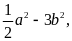 tại a = -2 ; b
tại a = -2 ; b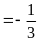 .
.
e.
P = 2x2
+ 3xy + y2
tại x =
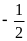 ;
y =
;
y =
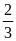 .
g. 12ab2;
tại a
.
g. 12ab2;
tại a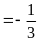 ;
b
;
b
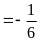 .
.
h.
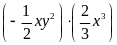 tại x =
2 ; y =
tại x =
2 ; y =
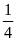 .
.
Bài 2 : Cho đa thức
a/ P(x) = x4 + 2x2 + 1; b/ Q(x) = x4 + 4x3 + 2x2 – 4x + 1;
Tính
: P(–1); P(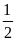 );
Q(–2); Q(1);
);
Q(–2); Q(1);
* Dạng 3 : Cộng, trừ đa thức nhiều biến
Phương pháp :
B1: viết phép tính cộng, trừ các đa thức.
B2: áp dung qui tắc bỏ dấu ngoặc.
B3: thu gọn các hạng tử đồng dạng ( cộng hay trừ các hạng tử đồng dạng)
Bài tập áp dụng:
Bài 1 : Cho 2 đa thức :
A = 4x2 – 5xy + 3y2 B = 3x2 + 2xy - y2
Tính A + B; A – B
Bài 2 : Tìm đa thức M, N biết :
a/ M + (5x2 – 2xy) = 6x2 + 9xy – y2 b/(3xy – 4y2)- N = x2 – 7xy + 8y2
* Dạng 4: Cộng trừ đa thức một biến:
Phương pháp:
B1: Thu gọn các đa thức và sắp xếp theo lũy thừa giảm dần của biến.
B2: Viết các đa thức sao cho các hạng tử đồng dạng thẳng cột với nhau.
B3: Thực hiện phép tính cộng hoặc trừ các hạng tử đồng dạng cùng cột.
Chú ý: A(x) - B(x) = A(x) + [- B(x)]
Bài tập áp dụng :
Bài 1: Cho đa thức
A(x) = 3x4 – 3/4x3 + 2x2 – 3 B(x) = 8x4 + 1/5x3 – 9x + 2/5
Tính : a/ A(x) + B(x); b/A(x) - B(x); c/ B(x) - A(x);
Bài 2: Cho các đa thức P(x) = x – 2x2 + 3x5 + x4 + x – 1
và Q(x) = 3 – 2x – 2x2 + x4 – 3x5 – x4 + 4x2
Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến.
Tính a/ P(x) + Q(x) b/ P(x) – Q(x).
* Dạng 5 : Tìm nghiệm của đa thức 1 biến
1. Kiểm tra 1 số cho trước có là nghiệm của đa thức một biến hay không?
Phương pháp :
B1: Tính giá trị của đa thức tại giá trị của biến cho trước đó.
B2: Nếu giá trị của đa thức bằng 0 thì giá trị của biến đó là nghiệm của đa thức.
2. Tìm nghiệm của đa thức một biến
Phương pháp :
B1: Cho đa thức bằng 0.
B2: Giải bài toán tìm x.
B3: Giá trị x vừa tìm được là nghiệm của đa thức.
Chú ý :
– Nếu A(x).B(x) = 0 => A(x) = 0 hoặc B(x) = 0
Nếu đa thức P(x) = ax2 + bx + c có a + b + c = 0
thì ta kết luận đa thức có 1 nghiệm là x = 1, nghiệm còn lại x2 = c/a.
Nếu đa thức P(x) = ax2 + bx + c có a – b + c = 0
thì ta kết luận đa thức có 1 nghiệm là x = –1, nghiệm còn lại x2 = -c/a.
Bài tập áp dụng :
Bài 1 : Cho đa thức F(x) = x4 + 2x3 – 2x2 – 6x + 5
Trong các số sau : 1; –1; 2; –2 số nào là nghiệm của đa thức f(x)
Bài 2 : Tìm nghiệm của các đa thức sau:
F(x) = 3x – 6; H(x) = –5x + 30 G(x) = (x-3)(16-4x)
K(x) = x2-81; M(x) = x2 +7x -8 N(x) = 5x2+9x+4
* Dạng 6 : Tìm hệ số chưa biết trong đa thức P(x) biết P(x0) = a
Phương pháp :
B1: Thay giá trị x = x0 vào đa thức.
B2: Cho biểu thức số đó bằng a.
B3: Tính được hệ số chưa biết.
Bài tập áp dụng :
Bài 1 : Cho đa thức P(x) = mx – 3. Xác định m biết rằng P(–1) = 2
Bài 2 : Cho đa thức Q(x) = -2x2 +mx -7m+3. Xác định m biết rằng Q(x) có nghiệm là -1.
* Dạng 7: Bài toán thống kê.
Câu 1. Điểm kiểm tra toán học kỳ I của học sinh lớp 7A được ghi lại như sau:
10 9 7 8 9 1 4 9
1 5 10 6 4 8 5 3
5 6 8 10 3 7 10 6
6 2 4 5 8 10 3 5
5 9 10 8 9 5 8 5
a) Dấu hiệu cần tìm ở đây là gì ?
b) Lập bảng tần số và tính số trung bình cộng.
c) Tìm mốt của dấu hiệu.
d) Dựng biểu đồ đoạn thẳng (trục hoành biểu diễn điểm số; trục tung biểu diễn tần số).
Câu 2. Một GV theo dõi thời gian làm bài tập(thời gian tính theo phút) của 30 HS của một trường(ai cũng làm được) người ta lập bảng sau:
Thời gian (x) |
5 |
7 |
8 |
9 |
10 |
14 |
|
Tần số (n) |
4 |
3 |
8 |
8 |
4 |
3 |
N = 30 |
a) Dấu hiệu là gì? Tính mốt của dấu hiệu?
b) Tính thời gian trung bình làm bài tập của 30 học sinh?
c) Nhận xét thời gian làm bài tập của học sinh so với thời gian trung bình.
Câu 3 : Số HS giỏi của mỗi lớp trong khối 7 được ghi lại như sau:
Lớp |
7A |
7B |
7C |
7D |
7E |
7G |
7H |
Số HS giỏi |
32 |
28 |
32 |
35 |
28 |
26 |
28 |
a. Dấu hiệu ở đay là gì? Cho biết đơn vị điều tra.
Lập bảng tần số và nhận xét.
Vẽ biểu đồ đoạn thẳng.
Câu 4: Tổng số điểm 4 môn thi của các học sinh trong một phòng thi được cho trong bảng dưới đây.
32 |
30 |
22 |
30 |
30 |
22 |
31 |
35 |
35 |
19 |
28 |
22 |
30 |
39 |
32 |
30 |
30 |
30 |
31 |
28 |
35 |
30 |
22 |
28 |
a/ Dấu hiệu ở đây là gì? Số tất cả các giá trị là bao nhiêu? số GT khác nhau của dấu hiệu ?
b/ Lập bảng tần số , rút ra nhận xét
c/ Tính trung bình cộng của dấu hiệu , và tìm mốt
Câu 5: Lớp 7A góp tiền ủng hộ đồng bào bị thiên tai. Số tiền góp của mỗi bạn được thống kê trong bảng (đơn vị là nghìn đồng)
1 |
2 |
1 |
4 |
2 |
5 |
2 |
3 |
4 |
1 |
5 |
2 |
3 |
5 |
2 |
2 |
4 |
1 |
3 |
3 |
2 |
4 |
2 |
3 |
4 |
2 |
3 |
10 |
5 |
3 |
2 |
1 |
5 |
3 |
2 |
2 |
a/ Dấu hiệu ở đây là gì?
b/ Lập bảng “tần số” , tính trung bình cộng
Câu 6. Thời gian làm bài tập của các hs lớp 7 tính bằng phút đươc thống kê bởi bảng sau:
4 5 6 7 6 7 6 4 6 7 6 8 5 6 9 10 5 7 8 8 9 7 8 8 8 10 9 11 8 9 8 9 4 6 7 7 7 8 5 8 
Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
Lập bảng tần số? Tìm mốt của dấu hiệu?Tính số trung bình cộng?
Vẽ biểu đồ đoạn thẳng?
Câu 7 : Số cơn bão hàng năm đổ bộ vào lãnh thổ Việt Nam trong 20 năm cuối cùng của thế kỷ XX được ghi lại trong bảng sau:
3 |
3 |
6 |
6 |
3 |
5 |
4 |
3 |
9 |
8 |
2 |
4 |
3 |
4 |
3 |
4 |
3 |
5 |
2 |
2 |
a/ Dấu hiệu ở đây là gì?
b/ Lập bảng “tần số” và tính xem trong vòng 20 năm, mỗi năm trung bình có bao nhiêu cơn bão đổ bộ vào nước ta ? Tìm mốt
c/ Biểu diễn bằng biểu đồ đoạn thẳng bảng tần số nói trên.
----------=*=*=*=*=*=*=-----------
II. PHẦN HÌNH HỌC:
A.KiÕn thøc c¬ b¶n
Nêu các trường hợp bằng nhau của hai tam giác, hai tam giác vuông? Vẽ hình, ghi giả thuyết, kết luận cho từng trường hợp?
Nêu định nghĩa, tính chất của tam giác cân, tam giác đều?
Nêu định lý Pytago thuận và đảo, vẽ hình, ghi giả thuyết, kết luận của cả hai định lý?
Nêu định lý về quan hệ giữa góc và cạnh đối diện trong tam giác, vẽ hình, ghi giả thuyết, kết luận.
Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghi giả thuyết, kết luận cho từng mối quan hệ.
Nêu định lý về bất đẳng thức trong tam giác, vẽ hình, ghi giả thuyết, kết luận.
Nêu tính chất 3 đường trung tuyến trong tam giác, vẽ hình, ghi giả thuyết, kết luận.
Nêu tính chất đường phân giác của một góc, tính chất 3 đường phân giác của tam giác, vẽ hình, ghi giả thuyết, kết luận.
Nêu tính chất đường trung trực của một đoạn thẳng, tính chất 3 đường trung trực của tam giác, vẽ hình, ghi giả thuyết, kết luận.
1) Các loại tam giác :(Đặc điểm, cách vẽ , tính chất , dấu hiệu nhận biết).
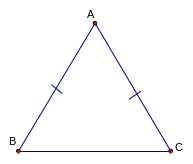
* Tam giác cân :
a) Định nghĩa : Tam giác cân là tam giác có hai cạnh bên bằng nhau b)Tính chất : trong tam giác cân hai góc ở đáy bằng nhau. c)
Cách vẽ :
+ vẽ cạnh đáy BC + Vẽ cung tròn tâm B có bán kính bất kỳ ( R > BC/2). +Vẽ cung tròn tâm C có cùng bán kính. Hai cung tròn cắt nhau tại điểm A. + Nối A với B ; A với C |
|
d) Dấu hiệu nhận biết : Chứng minh tam giác là tam giác cân thì chứng minh tam giác đó có :
+ Hai cạnh bằng nhau.
+ hai góc bằng nhau.
+ Hai đường trung tuyến ứng với hai cạnh của tam giác bằng nhau.
+ Đường trung tuyến xuất phát từ một đỉnh đồng thời là một trong các đường như đường phân giác của tam giác đó, đường trung trực , đường cao
* Tam giác đều :
a. Định nghĩa : tam giác đều là tam giác có ba cạnh bằng nhau. b.Tính chất : trong tam giác đều ba góc của tam giác bằng nhau bằng 600 c. Cách vẽ : Vẽ một cạnh bất kỳ ( BC). vẽ cung tròn tâm B bán kính bất kỳ ( R > BC/2). Vẽ cung tròn tâm C có cùng bán kính . Hai cung tròn cắt nhau tại A . Nối A với B ; A với C => được tam giác đều ABC. |
|
d. Dấu hiệu :
Chứng minh một tam giác có :
+ Ba cạnh bằng nhau.
+ Ba góc bằng nhau
+ là tam giác cân có một góc bằng 600
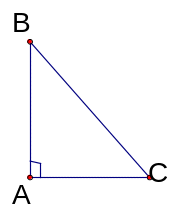
* Tam giác vuông :
a. Định nghĩa : Tam giác vuông là tam giác có một góc vuông. b. Tính chất : Hai góc nhọn của tam giác vuông phụ nhau. c. Cách vẽ : Vẽ góc vuông xOy. Lấy A thuộc tia Ox ; B thuộc tia Oy . Nối A với B được tam giác AO |
|
d. Dấu hiệu :
Để chứng minh một tam giác là tam giác vuông ta chứng minh tam giác đó có :
+ Một góc bằng 900
+ Có hai góc nhọn phụ nhau.
+ Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó.
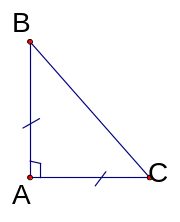
* Tam giác vuông cân :
a. Định nghĩa : Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau. b. Tính chất : Trong tam giác vuông cân hai góc nhọn bằng nhau bằng 450. c. Cách vẽ : Vẽ góc vuông xOy. Lấy A thuộc tia Ox ; B thuộc tia Oy sao cho OA =OB. Nối A với B được tam giác AOB vuông cân tại O. |
|
- Dấu hiệu : để chứng minh một tam giác là tam giác vuông cân ta cần chứng minh tam giác đó có :
+ Tam giác vuông có hai cạnh góc vuông bằng nhau.
+ Tam giác vuông có hai góc nhọn bằng nhau.
+ Tam giac vuông có một góc nhọn bằng 450
2) Các trường hợp bằng nhau của tam giác - tam giác vuông.
a. Các trường hợp bằng nhau của tam giác thường :
- Trường hợp cạnh – cạnh – cạnh : Nếu ba cạnh của tam giác này lần lượt bằng ba cạnh của tam giác kia thì hai tam giác bằng nhau.
- Trường hợp cạnh - góc - cạnh : Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác bừng nhau.
- Trường hợp bằng nhau góc - cạnh - góc : Nếu hai góc kề một cạnh của tam giác này lần lượt bằng hai góc kề một cạnh của tam giác kia thì hai tam giác đó bằng nhau.
b. Các trường hợp bằng nhau của tam giác vuông :
- Trường hợp 1 : Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giácvuông đó bằng nhau.
- Trường hợp 2 : Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Trường hợp 3 : Nếu một cạnh huyền và góc nhọn của tam giác vuông này lần lượt bằng cạnh huyền và góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Trường hợp 4 : Nếu cạnh huyền và cạnh góc vuông của tam giác vuông này lần lượt bằng cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
3) Quan hệ giữa cạnh và góc trong tam giác, đường xiên và hình chiếu, bất đẳng thức tam giác.
a. Định lý về bất đẳng thức tam giác:
* Định lý: Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.
*Nhận xét: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài hai cạnh còn lại.
b. Định lý về quan hệ giữa các cạnh và góc đối diện; đường xiên và hình chiếu:
* Định lý về quan hệ giữa góc và cạnh đối diện trong tam giác:
+ Định lý1: Trong một tam giác , góc đối diện với cạnh lớn hơn là góc lớn hơn.
+ Định lý 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
* Định lý về quan hệ giữa đường xiên và hình chiếu: Trong hai đường xiên kẻ từ một điểm nằmg ngoài một đường thẳng đến đường thẳng đó:
a. Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
b. Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
c. Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau, và ngược lại, nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
4) Các đường đặc biệt trong tam giác : ( Cách xác định, tính chất)
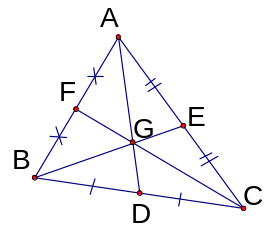
a. Đường trung tuyến trong tam giác :
* Định lý : Ba đường trung tuyến của một tam giác đồng quy tại một điểm. Điểm này cách mỗi đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
|
|
* Trọng tâm là giao điểm của ba đường trung tuyến trong tam giác.
* Cách xác định trọng tâm của tam giác:
- Vẽ hai đường trung tuyến của tam giác . giao điểm của hai đường trung tuyến là trọng tâm tam giác.
- Vẽ một đường trung tuyến của tam giác, trên đường trung tuyến xác định điểm G sao cho khoảng cách từ đỉnh đến G bằng 2/3 độ dài đường trung tuyến.
b) Định lý về tính chất ba đường phân giác trong tam giác :
+ Định lý: Ba đường phân giác của tam giác cùng đi qua một điểm. Điểm này cách đều 3 cạnh của tam giác.
|
|
c) Định lý về tính chất ba đường trung trực:
* Định lý: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều 3 đỉnh của tam giác.
|
|
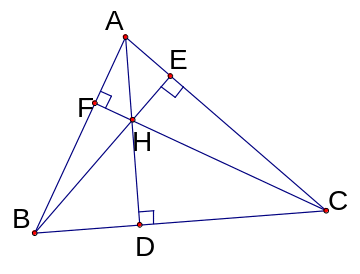
d) Định lý về ba đường cao của tam giác:
* Định lý: Ba đường cao của tam giác đồng quy tại một điểm.
* Trực tâm của tam giác là giao điểm ba đườn cao.
Xác định trực tâm: Xác định giao điểm 2 đường cao là trực tâm của tam giác.
|
|
5) Các điểm đặc biệt trong tam giác: ( Cách xác định, tính chất)
Tính chất đường phân giác của góc - tính chất đường trung trực của đoạn thẳng:
* Tính chất tia phân giác của góc: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc.
* Tính chất đường trung trực của đoạn thẳng: điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
B. MỘT SỐ PHƯƠNG PHÁP CHỨNG MINH HÌNH HỌC 7:
Dạng 1: Chứng minh hai tam giác bằng nhau. Từ đó suy ra các yếu tố tương ứng bằng nhau.
BÀI 1:
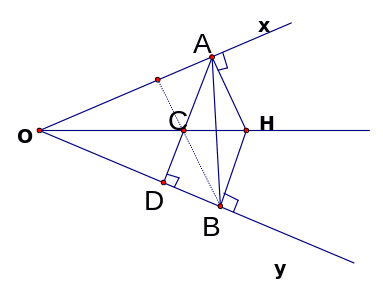
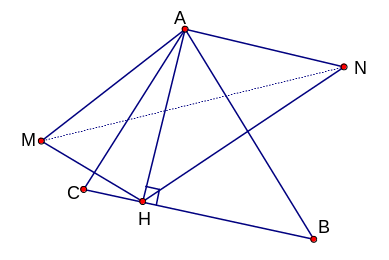
Cho góc nhọn xOy. Điểm H nằm trên tia phân giác của góc xOy. Từ H dựng các đường vuông góc xuống hai cạnh Ox và Oy (A thuộc Ox và B thuộc Oy).
a) Chứng minh tam giác HAB là tam giác cân
b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH. C/minh BC ⊥ Ox.
c) Khi góc xOy bằng 600, chứng minh OA = 2OD.
|
|
Chứng minh:
a) OAH = OBH ( cạnh huyền - cạnh góc vuông)
-> ẠH = BH ( 2 cạnh tương ứng) -> ABH cân tại H
b) AD Oy ; BH OY => AD // BH => CBA = BAH ( so le trong)
=>CB // AH mà AH Ox => CB Ox
c) ) OAH = OBH( c/m trên) -> AO = OB và AOB = 600 => AOB đều có AD OB
nên AD là trung tuyến ( t/chất đường trung tuyến, đường cao của tam giác đều)
OD = 1/ 2 OB hay OD = ½ OA hay OA = 2 OD
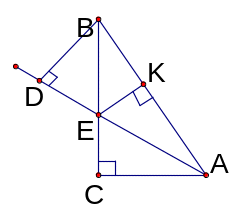
Bài 2:
Cho
∆ABC
vuông ở C,
có Aˆ
=
600
, tia phân giác của
góc
BAC. cắt BC ở E,
kẻ
EK
vuông
góc
với
AB.
(K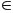 AB), kẻ
BD vuông góc AE (D
AB), kẻ
BD vuông góc AE (D
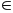 AE).
AE).
Chứng minh :
a) AK=KB
b) AD=BC
|
|
a. Chứng minh: AK = KB
Ta có: EAB = ½ BAC = ½ . 600 = 300 (1)
ABC có C = 900 ; A = 600 => B = 300 ( đlý tổng 3 góc trong một tam giác)(2)
Từ (1) và (2) => ∆AEB cân tại E => AE = EB
Xét ∆AEK và ∆BEK có EKB = AKE = 900( EK AB);EA = EB ( cmt); EK chung
=> ∆AEK = ∆BEK ( cạnh huyền – cạnh góc vuông) => BK = AK ( 2 cạnh tương ứng)
b) ∆ABC = ∆ BAE ( cạnh huyền - góc nhọn) => AD = BC ( 2 cạnh tương ứng)
Bài 3: Cho ∆ABC cân tại A và hai đường trung tuyến BM, CN cắt nhau tại K.
a) Chứng minh BNC= CMB
b)Chứng minh ∆BKC cân tại K
c) Chứng minh BC < 4.KM
|
|
∆BNC = ∆ CMB ( c.g.c)
∆BNC = ∆ CMB( c/ minh trên) => NCB = MBC mà ABC = BCA ( ∆ABC cân)
=> KBC = KCB ->∆ KBC cân tại K
Bài 4: Cho tam giác ABC vuông tại A, góc B có số đo bằng 600 . Vẽ AH vuông góc với BC, (H ∈ BC )
a. So sánh AB và AC; BH và HC;
b. Lấy điểm D thuộc tia đối của tia HA sao cho HD = HA. Chứng minh rằng hai tam giác AHC và DHC bằng nhau.
c. Tính số đo của góc BDC.
|
|
a. ∆ABC vuông tại A có B = 600 => C = 300
C < B => AB < AC ( quan hệ giữa góc và cạnh đối diện)
Vì AH BC và AB < AC 9 cmtrên) => HB < HC ( quan hệ giữa đường xiên và hình chiếu)
b) ∆ AHC = ∆ DHC ( c.gc) => AC = CD
c)∆ ABC = ∆DBC ( c.g.c) => CAB = CDB = 900
Bài 5: Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F.
a. Chứng minh ∆BEM= ∆CFM .
b. Chứng minh AM là trung trực của EF.
c. Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau tại D. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Bài 6:
|
|
a)∆ BEM = ∆CFM ( cạnh huyền – góc nhọn)
b) AB = AC ( ∆ABC cân tại A) ; BE = FC)∆ BEM = ∆CFM)
=>AE = À -> A thuộc đường trung trực của EF;
∆ BEM = ∆CFM => EM = FM => M thuộc đường trung trực của EF
=> AM là đường trung trực của EF
c) )∆ ABD = ∆ACD( cạnh huyền – cạnh góc vuông) => BAD = CAD => AD là phân giác của BAC ( 1)
∆ ABC cân AM là đường trung tuyến xuất phát từ đỉnh đồng thời là đường phân giác của BAC (2)
Từ (1) và (2) 3 điểm A; M; D thẳng hàng.
Dạng 2: So sánh góc, so sánh đoạn thẳng.
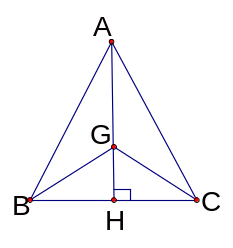
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Biết AB = 5 cm, BC = 6 cm.
a) Tính độ dài các đoạn thẳng BH, AH?
b) Gọi G là trọng tâm tam giác ABC. Chứng minh rằng ba điểm A, G, H thẳng hàng.
c) Chứng minh hai góc ABG và ACG bằng nhau.
|
|
a)∆ABC cân có AH là đường cao nên AH đồng thời là trung tuyến ( t/c tam giác cân)
=> H là trung điểm BC -> BH = HC = ½ BC = 1/ 2 . 6 = 3cm
∆ ABH vuông tại H có : AB2 = AH2 + B2 ( định lý py ta go)
=> AH2 = AB2 – BH2 = 25 – 9 = 16 -> AH = 4cm
b) AH là đường cao của tam giác cân xuất phát từ đỉnh đồng thời là trung tuyến
=> A; G; H thẳng hàng
c) ∆ ABG = ∆ ACG ( c.g.c) => ABG = ACG
Bài 2: Cho ∆ABC có AC > AB, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA . Nối C với D
a. Chứng minh ADC > DAC .Từ đó suy ra:MAB > MAC
b. Kẻ đường cao AH. Gọi E là một điểm nằm giữa A và H. So sánh HC và HB; EC và EB.
|
|
a)∆ AMB = ∆DMC ( c.g.c) => CD = AB mà AB < AC ( gt) => CD < AC
∆ ACD có CD < AC => CAD < ADC (1) mà CDA = MAB (2)
Từ (1) và (2) => MAB > MAC
b) ∆ ABC có AC > AB ; AH BC => HC > HB ( qhệ giữa đường xiên và hình chiếu)
HC > HB => EC > EB ( quan hệ giữa đường xiên và hình chiếu)
Bài 3: Cho ∆ABC (Â = 900) ; BD là phân giác của góc B (D∈AC). Trên tia BC lấy điểm E sao cho BA = BE.
a) Chứng minh DE ⊥ BE.
b) Chứng minh BD là đường trung trực của AE.
c) Kẻ AH ⊥ BC. So sánh EH và EC.
|
|
a)∆ ABD = ∆ EBD ( c.g.c) => BAD = BED mà BAD = 900 => BED = 900 hay DE BE
b) AB = BE 9 gt) => B thuộc đường trung trực của AE)∆ ABD = ∆ EBD( cm trên)
=> AD = DE => D thuộc đường trung trực của AE
=>BE là đường trung trực của AE
Bài 4: Cho tam giác nhọn ABC có AB > AC, vẽ đường cao AH.
a. Chứng minh HB > HC
b. So sánh góc BAH và góc CAH.
c. Vẽ M, N sao cho AB, AC lần lượt là trung trực của các đoạn thẳng HM, HN. Chứng minh tam giác MAN là tam giác cân.
|
|
a) ABC có AH BC ; AB > AC => HB > HC ( quan hệ giữa đường xiên và hình chiếu)
b) AB > AC (gt) => C > B => CAH < BAH ( vì CAH + C = BAH +B = 900)
c) CA là đường trung trực của MH => CM = AH ( t/c đường trung trực của đoạn thẳng)
AB là trung trực của HN => AH = AN ( t/ chất đường trung trực của đoạn thẳng)
=> AM = AN ( = AH) => ANM cân tại A
Dạng 3: Chứng minh các quan hệ hình học : Bằng nhau, song song, vuông góc.
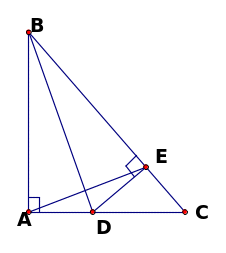
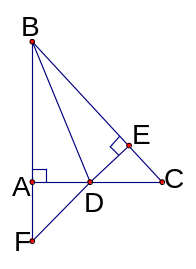
Bài 1: Cho ∆ ABC vuông tại A có BD là phân giác, kẻ DE ⊥ BC ( E∈BC ). Gọi F là giao điểm của AB và DE. Chứng minh rằng:
a) BD là trung trực của AE
b) DF = DC
c) AD < DC;
d) AE // FC.
|
|
a) ∆ ABD = ∆ EBD ( cạnh huyền – góc nhọn) => AD = DE => D thuộc đường trung trực của AE.
AB = BE -> B thuộc đường trung trực của AE
BD là đường trung trực của AE ( t/chất đường trung trực của đoạn thẳng)
b)∆ADF = ∆ FDC ( g.c.g) => DF = DC ( 2 cạnh tương ứng)
c) AD = DE ( c/minh a) và ∆ DEC có E = 900 => DC > DE ( quan hệ giữa góc và cạnh đối diện)
d)
AD = DE; AF = FC => FD = DC => ∆ FDC cân tại D =>
DFC =
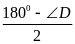 (1)
(1)
AD
= DE -> ∆ ADE cân tại D => DAE
=
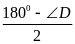 (2)
(2)
Từ
(1) và (2)
DFC = DAE
( =
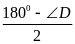 )
và hai góc ở vị trí so le trong => AE //FC
)
và hai góc ở vị trí so le trong => AE //FC
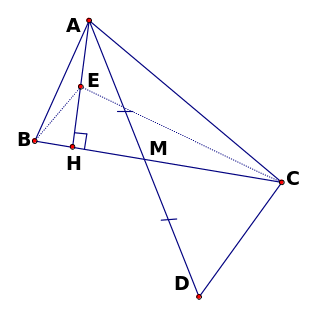
Bài
2: Cho
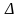 ABC
vuông cân ở A, M là trung điểm của BC, điểm E nằm giữa
M và C. Kẻ BH, CK vuông góc với AE (H và K thuộc đường
thẳng AE). Chứng minh rằng:
ABC
vuông cân ở A, M là trung điểm của BC, điểm E nằm giữa
M và C. Kẻ BH, CK vuông góc với AE (H và K thuộc đường
thẳng AE). Chứng minh rằng:
* BH = AK
*
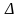 MBH
=
MBH
=
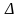 MAK
MAK
*
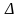 MHK
là tam giác vuông cân
MHK
là tam giác vuông cân
- HAB = KCA (CH – GN) -
Có
Từ
(1) và (2)
|
|
Bài
3: Cho
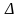 ABC,
gọi M và N theo thứ tự là trung điểm của AC và AB. Trên
tia đối của tia MB lấy điểm D sao cho MD = MB, trên tia
đối của tia NC lấy điểm E sao cho NE = NC. Chứng
minh rằng:
ABC,
gọi M và N theo thứ tự là trung điểm của AC và AB. Trên
tia đối của tia MB lấy điểm D sao cho MD = MB, trên tia
đối của tia NC lấy điểm E sao cho NE = NC. Chứng
minh rằng:
a. Ba điểm E, A, D thẳng hàng
b. A là trung điểm của ED
Hướng dẫn -
-
Từ
(1) và (2)
-
Từ chứng minh trên
|
|
c. Bµi tËp ¸p dông
Bài
1 : Cho
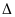 ABC cân tại A, đường cao AH. Biết AB=5cm, BC=6cm.
ABC cân tại A, đường cao AH. Biết AB=5cm, BC=6cm.
Tính độ dài các đoạn thẳng BH, AH?
Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng ba điểm A,G,H thẳng hàng?
Chứng minh:
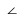 ABG
=
ABG
=
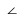 ACG?
ACG?
Bài
2: Cho
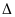 ABC cân tại A. Gọi M là trung điểm của cạnh BC.
ABC cân tại A. Gọi M là trung điểm của cạnh BC.
Chứng minh :
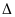 ABM =
ABM =
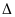 ACM
ACMTừ M vẽ MH
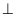 AB
và MK
AB
và MK
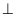 AC.
Chứng minh BH = CK
AC.
Chứng minh BH = CKTừ B vẽ BP
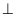 AC,
BP cắt MH tại I. Chứng minh
AC,
BP cắt MH tại I. Chứng minh
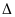 IBM cân.
IBM cân.
Bài
3 : Cho
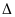 ABC vuông tại A. Từ một điểm K bất kỳ thuộc cạnh BC
vẽ KH
ABC vuông tại A. Từ một điểm K bất kỳ thuộc cạnh BC
vẽ KH
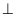 AC. Trên tia đối của tia HK lấy điểm I sao cho HI = HK.
Chứng minh :
AC. Trên tia đối của tia HK lấy điểm I sao cho HI = HK.
Chứng minh :
AB // HK
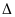 AKI
cân
AKI
cân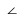 BAK
=
BAK
=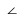 AIK
AIK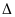 AIC
=
AIC
=
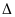 AKC
AKC
Bài
4 : Cho
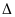 ABC cân tại A ( Â < 90o ), vẽ BD
ABC cân tại A ( Â < 90o ), vẽ BD
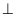 AC
và CE
AC
và CE
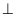 AB.
Gọi H là giao điểm của BD và CE.
AB.
Gọi H là giao điểm của BD và CE.
Chứng minh :
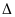 ABD =
ABD =
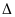 ACE
ACEChứng minh
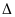 AED cân
AED cânChứng minh AH là đường trung trực của ED
Trên tia đối của tia DB lấy điểm K sao cho DK = DB. Chứng minh
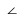 ECB =
ECB =
 DKC
DKC
Bài
5 : Cho
 ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên
tia đối của tia CA lấy điểm E sao cho BD = CE. Vẽ DH và
EK cùng vuông góc với đường thẳng BC. Chứng minh :
ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên
tia đối của tia CA lấy điểm E sao cho BD = CE. Vẽ DH và
EK cùng vuông góc với đường thẳng BC. Chứng minh :
HB = CK
 AHB
=
AHB
=
 AKC
AKCHK // DE
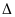 AHE
=
AHE
=
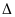 AKD
AKDGọi I là giao điểm của DK và EH. Chứng minh AI
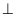 DE.
DE.
Bài 6: Cho góc xOy; vẽ tia phân giác Ot của góc xOy. Trên tia Ot lấy điểm M bất kỳ;
trên các tia Ox và Oy lần lượt lấy các điểm A và B sao cho OA = OB gọi H là giao điểm của AB và Ot. Chứng minh:
MA = MB
OM là đường trung trực của AB.
Cho biết AB = 6cm; OA = 5 cm. Tính OH?
Bài 7: Cho tam giác ABC có B = 900, vẽ trung tuyến AM. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh:
a)
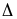 ABM
=
ABM
=
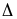 ECM
ECM
b) AC > CE.
c)
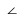 BAM >
BAM >
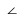 MAC
MAC
d) BE //AC
e)
EC
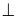 BC
BC
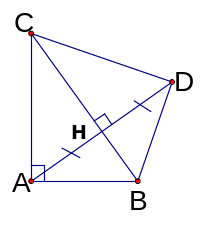
Bài 8 : Cho tam giác ABC cân ở A có AB = AC = 5 cm; kẻ AH BC ( H BC)
Chứng minh BH = HC và BAH = CAH
Tính độ dài BH biết AH = 4 cm.
Kẻ HD AB ( d AB), kẻ EH AC (E AC).
Tam giác ADE là tam giác gì? Vì sao?
Bài
9
: Cho
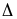 ABC
cân tại A. Trên tia đối của tia BC lấy điểm D, trên
tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng
minh:
ABC
cân tại A. Trên tia đối của tia BC lấy điểm D, trên
tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng
minh:
a)
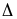 ADE
cân
ADE
cân
b)
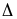 ABD
=
ABD
=
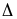 ACE
ACE
Bài 10 : Góc ngoài của tam giác bằng:
a) Tổng hai góc trong.
b) Tổng hai góc trong không kề với nó.
c) Tổng 3 góc trong của tam giác.
Bài 11 : Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD.
Chứng minh:
a) BE = CD.
b)
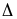 BMD
=
BMD
=
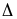 CME
CME
c) AM là tia phân giác của góc BAC.
Bài 12 : Cho ∆ ABC có AB <AC . Phân giác AD . Trên tia AC lấy điểm E sao cho AE = AB
a/ Chứng minh : BD = DE
b/ Gọi K là giao điểm của các đường thẳng AB và ED . Chứng minh ∆ DBK = ∆ DEC .
c/ ∆ AKC là tam giác gì ? Chứng minh
d/
Chứng minh DE
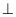 KC
.
KC
.
Bài
13 : Cho ∆ ABC có
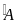 = 90° . Đường trung trực của AB cắt AB tại E và BC tại
F
= 90° . Đường trung trực của AB cắt AB tại E và BC tại
F
a/ Chứng minh FA = FB
b/
Từ F vẽ FH
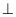 AC
( H
AC
( H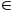 AC
) Chứng minh FH
AC
) Chứng minh FH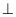 EF
EF
c/ Chứng minh FH = AE
d/
Chứng minh EH =
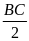 ; EH // BC
; EH // BC
Bài 14: Cho tam giác ABC (AB < AC) có AM là phân giác của góc A.(M thuộc BC).Trên AC lấy D sao cho AD = AB.
a. Chứng minh: BM = MD
b. Gọi K là giao điểm của AB và DM .Chứng minh: DAK = BAC
c. Chứng minh : AKC cân
d. So sánh : BM và CM.
Ngoài Đề Cương Ôn Tập HK2 Toán 7 Năm 2021-2022 Có Phân Dạng – Toán 7 thì các tài liệu học tập trong chương trình 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm







 ABCcân tại A
ABCcân tại A